【交叉熵损失torch.nn.CrossEntropyLoss详解-附代码实现】
CrossEntropyLoss
- 什么是交叉熵
- softmax
- 损失计算
- 验证
-
- CrossEntropyLoss 输入输出介绍
-
- 验证代码
- 多维交叉熵
-
- 验证代码
什么是交叉熵
交叉熵有很多文章介绍,此处不赘述。只需要知道它是可以衡量真实值和预测值之间的差距的,因而用交叉熵来计算损失的时候,损失是越小越好,它用数学公式表示是:
-P(x) log Q(x)
其中P(x)是真实值,Q(x)是预测值
当p(x)和Q(x)是矩阵的时候,就分别对其计算,然后求和即可
在pytorch中的交叉熵损失CrossEntropyLoss 包含了 两部分,softmax和交叉熵计算,下面分别介绍这两部分
softmax
一句话理解,是将预测值转成概率。通常经过神经网络计算出来的预测数据不是一个,举个例子:
比如一个二分类问题,一个输入计算出来的结果总是两个值(a, b)其中 a 表示1分类的得分,b 表示2分类的得分,多分类同样
比如一个翻译模型,每个时间步的输出是词表大小(a, b,…) 其中每个值表示词表中每个词的得分
而我们需要的是概率,不是分数,因此需要一个转换,要保证所有分类的概率和为1 softmax的做法:
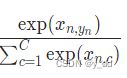
即:exp(某分数)/所有分类的exp后的分数
损失计算
计算完softmax,就可以用文中刚开始的 -P(x) log Q(x) 计算损失了,通常情况下,我们的真实值 p(x),也就是target 通常是one-hot编码的,举个例子:
比如二分类类的时候,target通常是(0,1)(1,0)
比如翻译模型,target通常是(0,…1…0)等
我们计算的时候不难发现target中为0经过乘法都是0了,因此最后只剩下正确类型的这个损失差距 最后公式可以演变成 - log Q(x)
一句话来说,交叉熵的损失值只关注了正确分类的差距
验证
自己实现了一下softmax和cross_loss,验证下上述理论的正确性,那就要介绍下torch.nn.CrossEntropyLoss
CrossEntropyLoss 输入输出介绍
可以翻看官网介绍
CLASStorch.nn.CrossEntropyLoss(weight=None, size_average=None, ignore_index=- 100, reduce=None, reduction=‘mean’, label_smoothing=0.0)
reduction是指损失计算方式,默认取平均mean,同时支持none,sum ,分别表示每一个损失不做其他操作、所有损失求求和
计算是target 的shape支持直接输入具体值,或者是索引形式,举个例子:
预测值: [0.8, 0.5, 0.2, 0.5]
target可以是 [1, 0, 0, 0] 或者索引形式 0
多样本也同样:
预测值:
[[0.8, 0.5, 0.2, 0.5],
[0.2, 0.9, 0.3, 0.2],
[0.4, 0.3, 0.7, 0.1],
[0.1, 0.2, 0.4, 0.8]]
target 可以是:
- 列表形式 torch.tensor([[1, 0, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 0],
[0, 0, 0, 1]], dtype=torch.float) - 索引形式: torch.tensor([0,1, 1, 3], dtype=torch.long)
验证代码
def soft_max(x):
x_exp = torch.exp(x)
partition = x_exp.sum(1, keepdim=True)
# 广播partition
return x_exp / partition
def cross_entropy(y, y_hat):
x = y_hat[range(len(y_hat)), y]
print("取出对应元素:", x, '真实label:', y)
return -torch.log(x)
y = torch.tensor([0, 2])
y_hat = torch.tensor([[0.1, 0.3, 0.6], [0.3, 0.2, 0.5]])
y_hat_softmax = soft_max(y_hat)
print(y_hat_softmax)
out = cross_entropy(y, y_hat_softmax)
print('手动计算的损失', out)
cr_loss = torch.nn.CrossEntropyLoss(reduction="none")
out = cr_loss(y_hat, y)
print('公式计算的损失', out)
输出如下:
手动计算的损失 tensor([1.3533, 0.9398])
公式计算的损失 tensor([1.3533, 0.9398])
结果一致,上述推论验证无问题
多维交叉熵
文本类数据通常是三维数据,预测通常是(batch_size,seq_length,num_vocab_size),而target是(batch_size,seq_length),此时需要预测的形状,通常使用permute操作成 (batch_size,num_vocab_size,seq_length)
验证代码
先使用上述验证过的,二维的交叉熵计算损失
cross_loss = torch.nn.CrossEntropyLoss(reduction='none')
input = torch.tensor([[4, 14, 19, 15],
[18, 6, 14, 7],
[18, 5, 3, 16]], dtype=torch.float)
target = torch.tensor([0, 3, 2])
loss = cross_loss(input, target)
数据均添加一维,变成三维数据
# shape [1, 3, 4]
input = torch.tensor([[[4, 14, 19, 15],
[18, 6, 14, 7],
[18, 5, 3, 16]]], dtype=torch.float)
input = input.permute(0, 2, 1)
# shape [1, 3]
target = torch.tensor([[0, 3, 2]])
loss = cross_loss(input, target)
打印上述两个代码的loss,损失一致:
loss is: tensor([15.0247, 11.0182, 15.1269]) # 这是二维的输出
loss is: tensor([[15.0247, 11.0182, 15.1269]]) # 这是三维的输出