【数据结构】红黑树的插入与验证
文章目录
- 一、基本概念
-
- 1.时代背景
- 2. 基本概念
- 3.基本性质
- 二、实现原理
-
- 1. 插入
-
- 1.1变色
- 1.2旋转+变色
-
- ①左旋
- ②右旋
- ③右左双旋
- ④左右双旋
- 2.验证
- 源码
- 总结
一、基本概念
1.时代背景
-
1972年鲁道夫·拜尔(Rudolf Bayer)发明了一种数据结构，这是一种特殊的B树4阶情况。这些树保持了从根到叶的所有路径，节点数量相同，创造了完美平衡的树。但是，它们不是二叉搜索树。拜耳在他的论文中称它们为“对称二元B树”。这是红黑树的起源。
-
在1978年的一篇论文“平衡树的二色框架”中，列奥尼达斯·吉巴斯（Leonidas J. Guibas ）和罗伯特·塞奇威克（Robert Sedgewick）从对称的二元B树中推导出了红黑树。选择“红色”是因为它是作者在施乐PARC工作时可用的彩色激光打印机产生的最好看的颜色。吉巴斯的另一个回应说，这是因为他们可以使用红色和黑色的笔来画树。
第一张为——列奥尼达斯·吉巴斯，第二张为——罗伯特·塞奇威克。
- 1993年，Arne Andersson引入了右倾树的想法，以简化插入和删除操作。
- 1999年，Chris Okasaki展示了如何使插入操作纯粹功能化。它的平衡功能只需要处理 4 个不平衡情况和一个默认平衡情况。
详细请看：维基百科
2. 基本概念
红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或
Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路 径会比其他路径长出俩倍，因而是接近平衡的。
- 实现平衡的关键：
最长路径小于等于最短路径的两倍。
3.基本性质
- 每个结点不是红色就是黑色
根节点是黑色的如果一个节点是红色的，则它的两个孩子结点是黑色的(如果一个结点是黑色的，则其两个孩子可以是红的也可以是黑的。)对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点- 每个叶子结点都是黑色的(此处的叶子结点指的是空结点）
强调：2，3，4点是有关联的，且是最关键的3点。
- 假设根节点如果是红的，那么插入的结点就是只能是黑的（3），那么就违背了（4）。
- 对于3分析，孩子结点为空，但空节点也被理解成黑色(5)，因此(5)是用来辅助(3)的。但是这单这一条分析不出来每次插入的是什么颜色的结点，得结合(4)分析。
- 对于4分析，可推理出两个结论——
1 . 插入结点必须为红色的，若是插入黑的，每条路径的黑色结点必然变化。
2 . 满足最长路径小于最短路径的两倍(概念)。对此点可以看做间隔问题，即n个数之间（不算头一个数），有n个间隔，即n个黑结点（不算根节点），之间最多有n个红结点。
二、实现原理
1. 插入
1.1变色
根本逻辑：基于每条路径的黑色结点不变。
第一种变色方式：
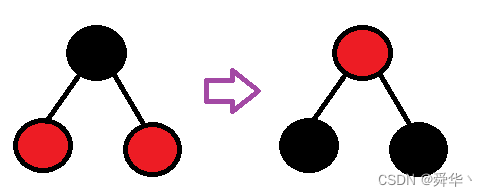
这样变，是不是每条路径的黑色结点数没变呢？
那这样变的前提是什么呢？
- 黑色结点的左右孩子为红且不为空。
那什么时候发生变色呢？
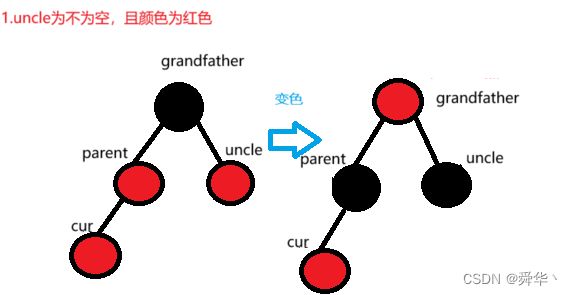
- 基于性质3，
红色结点的两个孩子必须为黑，但由4我们可以推出每次插入结点必须为红，那这时候我们按照4的原则进行处理，使处理结果符合3即可，怎么处理，就是进行变色。
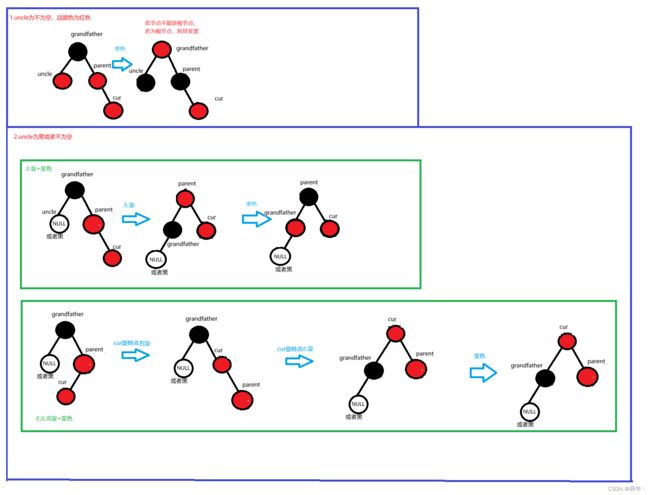
此时，parent的右边进行插入新节点，且parent在grandfather的左边。
此时在parent的右边进行插入，且parent为grandfather的左节点。
- 总结
- 变色的前提是每条路径的黑色结点不变
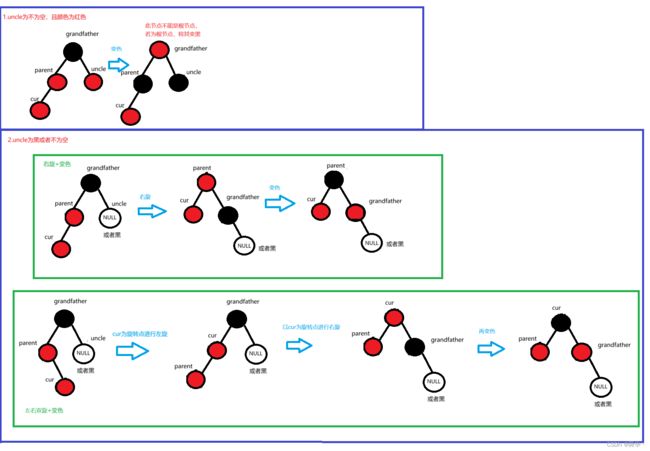
- uncle非空且为红，且parent为红(条件)。变grandfather为红，parent与uncle为黑(操作)。
继续分析，如果grandfather为红，其父节点是否可能为红呢？
- 答案是可能的。
因此我们需要继续往上更新：
- 更新cur为grandfather
- parent为cur的parent
接着分析，如果grandfather为根节点呢？
- 由于性质2，我们需要再次修改根节点的颜色为黑。
1.2旋转+变色
前面我们分析了一种简单的只需变色的情况，我们下面接着分析另外一种情况。
第二种变色需要在旋转的基础上进行分类讨论，具体情况有四种。
①左旋
补充：当uncle为黑结点时，parent的左子树不为空且根节点为黑色，cur的左右子树同理，这里不过多分析了,作为了解即可，因为具体情况过多分析容易提高理解难度。
- 开始时parent在grandfather右边，且cur在parent的右边
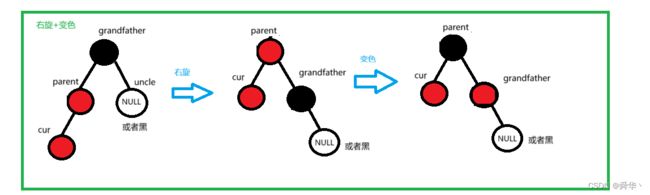
②右旋
对uncle的补充同左旋
- 开始时parent在grandfather左边，且cur在parent的左边
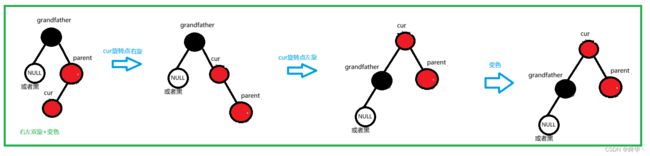
③右左双旋
对uncle的补充同左旋
- 开始时parent在grandfather的右边，且cur在parent的左边
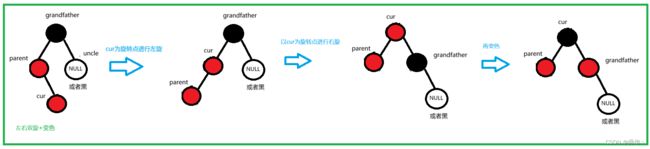
④左右双旋
对uncle的补充同左旋
-
开始时parent在grandfather的左边，且cur在parent的右边
-
总结
根据parent的位置我们可以大致分为两种情况：
-
parent在grandfather的左边
-
parent在grand的右边
其实不难看出，AVL和红黑树都会进行旋转，只是AVL树旋转后处理的是平衡因子，红黑树旋转后处理的是变色，归根结底终究都是为了让树达到平衡。
- 核心代码
//判断是否要进行旋转变色
//当父节点为红色说明要进行判断
while (parent && parent->_col == RED)
{
//爷爷结点
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)//如果uncle存在且为红色
{
//变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续往上迭代进行分析
cur = grandfather;
parent = cur->_parent;
}
else//如果uncle不存在或者为黑色
{
//旋转
if (parent->_left == cur)
{
RotateR(grandfather);
parent->_col = BLACK;
cur->_col = grandfather->_col = RED;
}
else
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
parent->_col = grandfather->_col = RED;
}
break;
}
}
else//grandfather->_right == parent
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
//变色
grandfather->_col = RED;
parent->_col = uncle->_col = BLACK;
//往上更新
cur = grandfather;
parent = cur->_parent;
}
else
{
if (parent->_right == cur)
{
//旋转
RotateL(grandfather);
//变色
parent->_col = BLACK;
grandfather->_col = cur->_col = RED;
}
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = parent->_col = RED;
}
break;
}
}
}
- 插入代码
bool insert(const pair<Key, Val>& val)
{
//第一步：插入操作
//如果根节点为空
if (_root == nullptr)
{
_root = new Node(val);
_root->_col = BLACK;
return true;
}
else
{
Node* cur = _root, * parent = _root;
while (cur)
{
if (cur->_key > val.first)
{
parent = cur;
cur = cur->_left;
}
else if (cur->_key < val.first)
{
parent = cur;
cur = cur->_right;
}
else
{
return false;
}
}
cur = new Node(val);
if (parent->_key > val.first)
{
parent->_left = cur;
}
else
{
parent->_right = cur;
}
//更新新增结点的_parent
cur->_parent = parent;
//判断是否要进行旋转变色
//当父节点为红色说明要进行判断
while (parent && parent->_col == RED)
{
//爷爷结点
Node* grandfather = parent->_parent;
if (grandfather->_left == parent)
{
Node* uncle = grandfather->_right;
if (uncle && uncle->_col == RED)
//如果uncle存在且为红色
{
//变色
parent->_col = uncle->_col = BLACK;
grandfather->_col = RED;
//继续往上迭代进行分析
cur = grandfather;
parent = cur->_parent;
}
else//如果uncle不存在或者为黑色
{
//旋转
if (parent->_left == cur)
{
RotateR(grandfather);
parent->_col = BLACK;
cur->_col = grandfather->_col = RED;
}
else
{
RotateL(parent);
RotateR(grandfather);
cur->_col = BLACK;
parent->_col = grandfather->_col = RED;
}
break;
}
}
else//grandfather->_right == parent
{
Node* uncle = grandfather->_left;
if (uncle && uncle->_col == RED)
{
//变色
grandfather->_col = RED;
parent->_col = uncle->_col = BLACK;
//往上更新
cur = grandfather;
parent = cur->_parent;
}
else
{
if (parent->_right == cur)
{
//旋转
RotateL(grandfather);
//变色
parent->_col = BLACK;
grandfather->_col = cur->_col = RED;
}
else
{
RotateR(parent);
RotateL(grandfather);
cur->_col = BLACK;
grandfather->_col = parent->_col = RED;
}
break;
}
}
}
//根节点可能为红色,不管红色还是黑色都弄成黑色
_root->_col = BLACK;
return true;
}
}
2.验证
- 原理
- 根节点不能为红
- 每条路径的黑色结点数相同
- 每条路径不能出现连续的红色结点。
- 代码
bool _IsRBTree(Node* root)
{
if (root == nullptr)
return true;
//根节点是黑色的
if (root->_col == RED)
return false;
//各个路径的黑色结点数是相同的，因此设立一个基准进行比较合适，
//再对树进行遍历求每个路径的黑色结点的数量，最后比较即可。
int benchmark = 0;
Node* cur = root;
while (cur)
{
if (cur->_col == BLACK)
benchmark++;
cur = cur->_left;
}
return Check(root);
}
bool Check(Node* root, int BCount,int benchmark)
{
if (root == nullptr)
{
//验证基准值是否等于黑色结点数
//只要有一个不是，即不是红黑树。
if (BCount != benchmark)
return false;
return true;
}
//求每条黑色结点的个数
if (root->_col == BLACK)
BCount++;
//验证性质3，即不能有连续的红色结点。
if (root->_col == RED && root->_parent
&& root->_parent->_col == RED)
{
return false;
}
return Check(root->_left,BCount,benchmark)
&& Check(root->_right, BCount, benchmark);
}
源码
#pragma once
#include总结
红黑树的理解较AVL树抽象，需要画图分析，不过有了AVL树旋转的基础，这里的难度要下降不少。还是与之前一样，只要图画的好，代码跑不了，所以这里的关键就在于画图。
总之，今天的分享到这里就结束了，如果感觉有所帮助，不妨点个赞鼓励一下吧！