【LeetCode学习笔记】137. 只出现一次的数字 II

1. 题目描述

给定一个非空整数数组，除了某个元素只出现一次以外，其余每个元素均出现了三次。找出那个只出现了一次的元素。

示例 1:

输入: [2,2,3,2]
输出: 3

示例 2:

输入: [0,1,0,1,0,1,99]
输出: 99

---

2. 解题记录

2.1【2020/03/23 - 36ms - 96.81%】

        使用 collections 模块的 Counter 类来构造 HashMap 是十分高效的，对输入数组 nums 从小到大排序，返回最后一个数字，即出现次数为 1 的数字。该方法在 136.只出现一次的数字 中也适用。

class Solution:
    def singleNumber(self, nums):
        # 实例化 Counter 类构建 Hashmap
        hashmap = collections.Counter(nums)
        # 按 value 对 Hashmap 从大到小排序, 选择最后一个 (即 value 最小的元素的 key 值)
        return hashmap.most_common()[-1][0]

---

2.2【2020/03/23 - 40ms - 91.58%】

        事实上，时间主要耗费在遍历过程中，为此，需要在尽量少的遍历次数下完成查找。以下使用了一种常见思路 —— “状态指示器 indicator”，先对列表排序，再遍历，但凡有元素被遇见的次数不满足3，即为仅出现一次的数。这等同于使用 nums[i] 、 nums[i+1] 、nums[i+2] 这种长度为3的滑动窗口逐次判断。

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        nums.sort()  # 从小到大排序
        cur_num = nums[0]  # 初始cur_num

        if len(nums) == 1 or cur_num != nums[1]:  # 特殊情况, 如果第一位就是
            return cur_num

        indicator = 3  # 初始计数器/状态指示器
        for i in nums:
            if i == cur_num:  # 如果本值等于cur_num
                indicator -= 1  # 计数-1
            elif indicator == 2:  # 如果只出现过一次(计数只-1)
                return cur_num  # 就是它
            else:
                cur_num = i  # 否则, 又遇到三个数
                indicator = 2  # 因为本次判断见过一次了, 只需要再见两次

        # 最后一位数
        return cur_num

        这类方法具有较强的泛化性，在 136.只出现一次的数字 中也适用，但性因题而异，毕竟具体问题具体分析嘛~

---

2.3【2020/03/23 - 32ms - 98.90%】

        自己的方法试完了，就学习一下其他的优秀解法，其中一种方法是数学法。假设输入数组 nums 由四种数字构成 (当然，无论由几种数字构成都满足)，即有 nums = [x, x, x, y, y, y, z, z, z, s]，那么唯一的数字 s 可由下式得到：

                                             

        分子中，被减数可由 3 * sum(set(nums)) 得到，减数则直接有 sum(nums)，如下所示：

class Solution:
    def singleNumber(self, nums):
        return (3 * sum(set(nums)) - sum(nums)) // 2

这基本是最快的方法了。不得不说，仅会编程仅得形骸，善用数学方得神韵！数学能力决定上限。

---

2.4 【2020/03/23 - 】

引用一个没见过的思路，使用位运算实现，只需要 O(1) 的空间复杂度。首先，Python 中常见的位运算符有：

&	按位与运算符 (AND)：参与运算的两个值，如果两个相应位都为1，则该位的结果为1，否则为0
|	按位或运算符 (OR)：只要对应的二个二进位有一个为1时，结果位就为1
~	按位非运算符 (NOT)：对数据的每个二进制位取反，即把1变0，把0变1；~x 类似于 -x-1
^	按位异或运算符 (XOR)：当两对应的二进位相异时，结果为1；相同时，结果为0
<<	按位左移运算符：运算数的各二进位全部左移若干位，由 << 右边数字指定移动位数，高位丢弃，低位补0
>>	按位右移运算符：把 >> 左边的运算数的各二进位全部右移若干位，>> 右边的数字指定了移动位数

        其中，异或 (XOR) 可以检测出现奇数次的位，如 1、3、5 、7 等，这其中存在两个重要性质：

	任意数字与 0 异或运算，结果不变
	任意数字与自身异或运算，结果为 0

        因此根据上述性质，异或 (XOR) 可检测出现 1 次或 3 次出现的位。

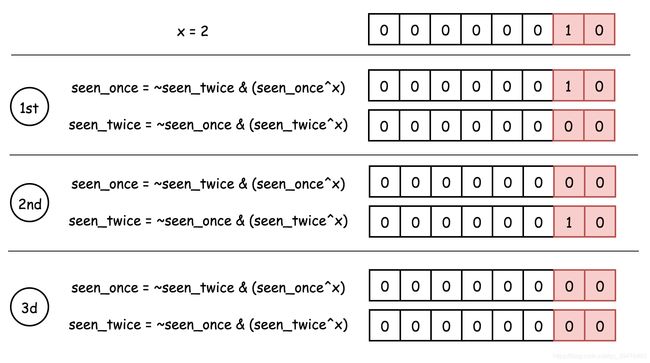
但为进一步区别，还需要使用两个指示器，或者说是位掩码 seen_once 和 seen_twice。

仅当 seen_twice 未变时，改变 seen_once；仅当 seen_once 未变时，改变 seen_twice。

        从而指示器/位掩码 seen_once 最终只留下出现一次的数字。

class Solution:
    def singleNumber(self, nums: List[int]) -> int:
        seen_once = seen_twice = 0

        for num in nums:
            # first appearance: 
            #     add num to seen_once 
            #     don't add to seen_twice because of presence in seen_once
            
            # second appearance: 
            #     remove num from seen_once 
            #     add num to seen_twice
            
            # third appearance: 
            #     don't add to seen_once because of presence in seen_twice
            #     remove num from seen_twice
            seen_once = ~seen_twice & (seen_once ^ num)
            seen_twice = ~seen_once & (seen_twice ^ num)

        return seen_once

        当然，正常人应该想不到这么做吧？！

        引文链接 https://leetcode-cn.com/problems/single-number-ii/solution/zhi-chu-xian-yi-ci-de-shu-zi-ii-by-leetcode/