第三章 微分中值定理与导数的应用

参考文献

高昆轮 2019考研数学

点进去你会发现新大陆：考研数学证明题的那些事CSDN、知乎

一、微分中值定理

罗尔定理

$$\begin{gathered} \text{ 设 }f(x)\text{ 满足 }\{\begin{array}{l}[a,b]\text{ 上连续 }\\ (a,b)\text{ 内可导 }\\ f(a)=f(b)\end{array} \\ ,\text{ 则 }\exists \xi \in (a,b),\text{ 使 }{f}^{\prime }(\xi )=0 \end{gathered}$$

$\{\begin{array}{l}闭区间连续\\ 开区间可导\\ 端点值相等\end{array}$

重点：端点值相等，$f(\xi )=0$

零点定理和介值定理也是闭区间连续

---

题型
【例1】证明等式关于函数以及函数的二阶导，无一阶导，两个端点值相等，因此想到罗尔定理$f^{\prime }(x)=0$

由端点值相等，猜测罗尔定理，$f^{\prime }(x)=0$，等式能否构造为导数形式
原函数保留，二阶导由一阶导的导数得到，因此构造的形式关于原函数及一阶导

【例2】显然是罗尔定理，所以还是构造为导数形式
由导数运算法则，等式似乎缺少系数，问题：什么求导后能被消去的，答：以e为底的指数

小结：罗尔定理证明题，一般是构造为导数形式

【例3】不正确小结：给定条件可知为罗尔定理，需证明两个问题，第一个是零点定理或介值定理，第二个是罗尔定理
对于第一个问题，已知使用零点定理，也是根据等式构造函数（非导数形式），判断是否异号，是则存在零点，否则无。
对于第二个问题，还是构造为导数形式，不过是广义的。广义无常，本质不变。

【例4】条件中无端点值相等，其在证明中，轮换形式即端点值相等。因此对于这种无端点值相等的题目，找到轮换形式，然后构造函数即可。此法称之为常数k值法，此题还可用拉格朗日中值定理证明。

【习题11】显然必须要用到罗尔定理，但是两个端点值并不相等，引用介值定理使得端点值相等

---

总结
考察罗尔定理的三种形式$\{\begin{array}{l}端点值相等\\ f^{\prime }(\xi )=0\\ 端点值相等和f^{\prime }(\xi )=0\end{array}$

端点值相等：常数k值法

$f^{\prime }(\xi )=0$:考得较多，同时也会考察零点定理（构造函数）等，构造导数函数，或构造广义导数函数

---

拉格朗日中值定理

$$\begin{gathered} \text{ 设 }f(x)\text{ 满足 }\{\begin{array}{l}[a,b]\text{ 上连续 }\\ (a,b)\text{ 内可导 }\end{array} \\ ,\text{ 则 }\exists \xi \in (a,b),\text{ 使 }{f}^{\prime }(\xi )=\frac{f(b)-f(a)}{(b-a)}. \end{gathered}$$

无端点值相等

---

题型：
情形1:遇到$f(b)-f(a)$
情形2:想把$f(x)$和$f^{\prime }(x)$联系在一起或$f(x)$和$f^{\prime \prime }(x)$联系在一起

情形1:具有相同的函数
求极限【例5，例6】，证明题（广义情形1）【例7】

情形2:【例8，例9】
对于例8，已知使用拉格朗日中值定理，相加的形式，且存在零点，拆分然后用拉格朗日
例9，已知使用拉格朗日，二阶导是一阶导的导数，嵌套使用拉格朗日

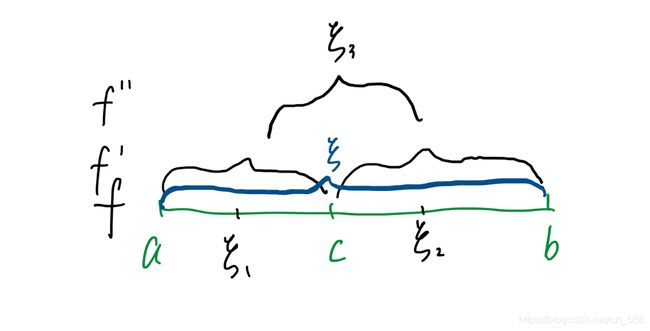
蓝线为情形1，黑线为情形2

---

总结：无论是情形1还是情形2，无法逃脱$f(b)-f(a)$，情形2小三插入裂开了

---

柯西中值定理

$$\begin{gathered} \text{ 设 }f(x)、g(x)\text{ 满足 }\{\begin{array}{l}[a,b]\text{ 上连续 }\\ (a,b)\text{ 内可导 }\\ g^{\prime }(x)\ne 0\end{array} \\ ,\text{ 则 }\exists \xi \in (a,b),\text{ 使 }\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime }(\xi )}{g^{\prime }(\xi )}. \end{gathered}$$

$g(a)\ne g(b)$

两个拉格朗日的比值
$$\frac{f(b)-f(a)}{g(b)-g(a)}=\frac{f^{\prime }(\xi )(b-a)}{g^{\prime }(\xi )(b-a)}$$

---

并不是显形给出，特别关注函数为0的时候

考到就废了

---

泰勒定理

区间
带拉格朗日余项的n阶泰勒公式
邻域
带佩亚诺余项的n阶泰勒公式

带拉格朗日余项的n阶泰勒公式
研究：区间
题型：证明不等式；研究最值；

带佩亚诺余项的n阶泰勒公式
研究：领域
题型：极限；高阶导数；极值

---

多少阶多少阶可导
高阶导数-佩亚诺余项泰勒公式
直接展开，找点替换
已知导数值的点作$x_0$
已知函数值或特殊值点（端点、中间点）作$x$
如例15.$f(-1)=0,f(1)=1$作$x$，$f^{\prime }(0)=0$作$x_0$
（$x_0=0,x=-1,x=1$）;
例16.$|f^{\prime \prime }(x)|$作$x_0$，对$\forall x\in [0,1]$作$x$
$(x_0=x,x=0,x=1)$

---

二、导数的应用

1.单调性的判定

导数大于0，单调增
否则相反

2.极值的定义

3.极值的必要条件

4.极值的第一充分条件

一阶导

5.极值的第二充分条件

二阶导

6.求函数的最值

求出驻点和不可导点，并求出这些点的函数值
求出端点的函数值
比较所有函数值，最大的为最大值，最小的为最小值

注：仅有一个极值，此极值就是最值

7.凹凸性及拐点的定义

$f(E)>E[f]$为凸

连续曲线的凹弧与凸弧的分界点称为曲线的拐点

8.凹凸性的判定

二阶导大于0，为凹
二阶导小于0，为凸，一阶导单调减，即斜率逐渐减小

9.拐点的必要性

10.拐点的第一充分条件

11.拐点的第二充分条件

---

题型一 用导数研究函数（曲线）的性态

【例1】导数判断单调性，f(x)未知，拉格朗日

单调性
极值
（最值）
（凹凸性）
驻点
参数方程
拐点（研究工具为二阶导，研究驻点和不存在的点两端是否异号，是则为拐点，驻点和不存在的点较多时画表，随机代入点判断二阶导大于0还是小于0），注意：一定是连续曲线，不连续咱不要

---

拐点二阶导判断是否异号（二阶导等价于凹凸性，因此在做选填题时，一是看曲线穿过横轴的个数，二是凹凸性变化（7.凹凸性和拐点的定义）

---

题型二 证明不等式
（题目较短）

根据泰勒公式有如下不等式关系：
$$\begin{gathered} \sin x<x<\tan x \\ \frac{x}{1+x}<\ln (1+x)<x \end{gathered}$$

单调性（根据不等式构造函数，利用函数的单调性便可证明）
（【例7】当一阶导无法判断正负号时，尝试二阶导，如果还是无法判断，则使用不等式关系，或者根据条件判断）
（【例8】指数求导不方便，取对数）
（【例9】另解：变量在一侧，常量在另一侧）
（【例11】常数不等式，常数导数为0，将常数改成变量，即变量不等式）

最值
（【例10】驻点和端点）

---

小结：
单调性
1.指数取对数；常数改成变量（皆不是略去此步）
2.单调性是证明不等式的重要工具
3.还需懂得判断导数的正负

最值
求导，比较驻点值和端点值

---

题型三 方程的根（零点问题）

【例12】隐式给出端点，零点定理

【例13】死死盯着端点；既然零点定理无法用，那就罗尔定理好了，两个方程很像，实际上是导数关系，代入端点验证（或者反推），原函数的导数就是导数方程的零点（根）

【例14】有一个端点值小于0，显然是零点定理，但是对于这么抽象的题目，另一个端点值的符号很难判断。梳理已有的条件，弄清你的目的，已知$f(a)、f^{\prime }(x)$,目的$f(a+\frac{|f(a)|}{k})$，因此可以使用拉格朗日即可判断$f(a+\frac{|f(a)|}{k})$

【例15】没有端点，求参数的取值范围，分类讨论；另解：分离参数法（易）

---

小结：
既然知道用零点定理或罗尔定理了，给我狠狠的盯住端点
1.先找到端点
2.判断是用零点定理还是罗尔
3.1.零点定理
一个端点已给定，拉格朗日+零点定理
3.2.罗尔定理
罗尔定理处理较麻烦，根据题目找到需证明的原函数

无端点+取值范围
分类讨论，零点定理；分离参数法

---

三、渐近线

1.水平渐近线

$y=a$

2.铅直渐进线

$x=x_0$

3.斜渐近线

$y=kx+b$
先算出k,再算b

	趋于	是+1	否+0
水	$\infty$	常数
铅	无定义点（常数）	$\infty$
斜	$\pm \infty$	k,b常数

【例16】要分左右极限的三种情况

【例17】随时用拉格朗日

四、曲率及曲率半径