LeetCode_模拟_中等_2596.检查骑士巡视方案

1.题目

骑士在一张 n x n 的棋盘上巡视。在有效的巡视方案中，骑士会从棋盘的左上角出发，并且访问棋盘上的每个格子恰好一次 。

给你一个 n x n 的整数矩阵 grid ，由范围 [0, n * n - 1] 内的不同整数组成，其中 grid[row][col] 表示单元格 (row, col) 是骑士访问的第 grid[row][col] 个单元格。骑士的行动是从下标 0 开始的。

如果 grid 表示了骑士的有效巡视方案，返回 true；否则返回 false。

注意，骑士行动时可以垂直移动两个格子且水平移动一个格子，或水平移动两个格子且垂直移动一个格子。下图展示了骑士从某个格子出发可能的八种行动路线。

示例 1：

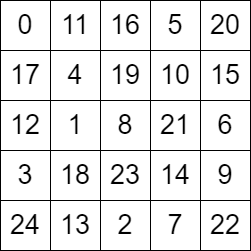
输入：grid = [[0,11,16,5,20],[17,4,19,10,15],[12,1,8,21,6],[3,18,23,14,9],[24,13,2,7,22]]
输出：true
解释：grid 如上图所示，可以证明这是一个有效的巡视方案。

示例 2：

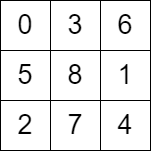
输入：grid = [[0,3,6],[5,8,1],[2,7,4]]
输出：false
解释：grid 如上图所示，考虑到骑士第 7 次行动后的位置，第 8 次行动是无效的。

提示：
n == grid.length == grid[i].length
3 <= n <= 7
0 <= grid[row][col] < n * n
grid 中的所有整数 互不相同

2.思路

（1）模拟
用 indices 存储单元格的访问顺序，其中 indices[i] 表示骑士在经过第 i − 1 次跳跃后的位置。由于骑士的行动是从下标 0 开始的，因此一定需要满足 grid[0][0] = 0，接下来依次遍历 indices 中的每个元素。由于 indices[i] 是一次跳跃的起点，indices[i + 1] 是该次跳跃的终点，则依次检测每一次跳跃的行动路径是否为「日」字形即可。

相关题目：
LeetCode_动态规划_中等_688.骑士在棋盘上的概率

3.代码实现（Java）

//思路1————模拟
class Solution {
    public boolean checkValidGrid(int[][] grid) {
        if (grid[0][0] != 0) {
            return false;
        }
        int n = grid.length;
        // indices[i] 表示骑士在经过第 i − 1 次跳跃后的位置
        int[][] indices = new int[n * n][2];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                indices[grid[i][j]][0] = i;
                indices[grid[i][j]][1] = j;
            }
        }
        for (int i = 1; i < n * n; i++) {
            int nx = Math.abs(indices[i][0] - indices[i - 1][0]);
            int ny = Math.abs(indices[i][1] - indices[i - 1][1]);
            if (nx * ny != 2) {
                return false;
            }
        }
        return true;
    }
}