java十大排序算法

十大排序算法在面试java过程中想必或多或少都会有。尤其是在笔试题上，有些大厂就让你现场写个十大排序。是不是一下子整懵了。。。

目录

一、首先先介绍下十大排序算法：

1、算法分类

2 、算法复杂度

3、 相关概念

二、详细分析各个算法

1、冒泡排序

2、选择排序

3、快速排序

4、插入排序

5、计数排序

6、希尔排序

7、堆排序

8、归并排序

9、桶排序

10、基数排序

---

一、首先先介绍下十大排序算法：

1、算法分类

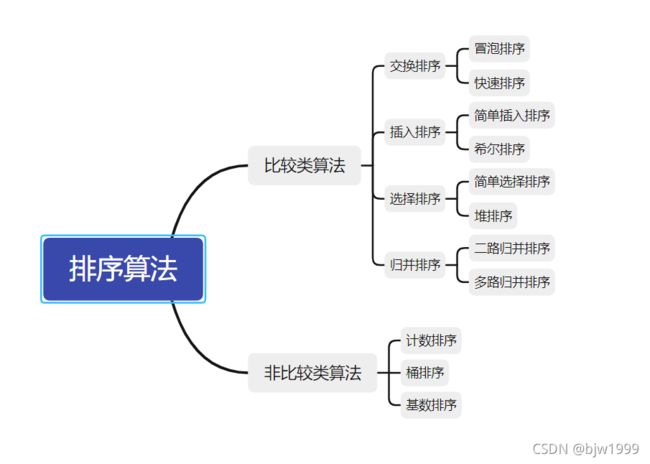
十种常见排序算法可以分为两大类：

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破O(nlogn)，因此也称为非线性时间比较类排序。
• 非比较类排序：不通过比较来决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较类排序。 

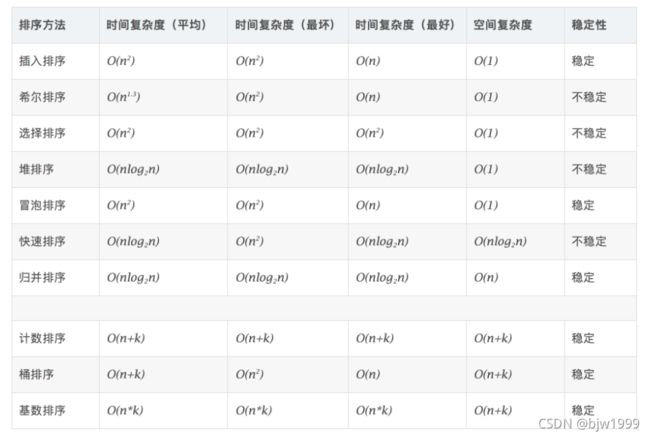
2 、算法复杂度

3、 相关概念

• 稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
• 不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
• 时间复杂度：对排序数据总的操作次数。反映当n变化时，操作次数呈现什么规律。
• 空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。
• 算法的时间与空间复杂度（一看就懂） - 知乎

二、详细分析各个算法

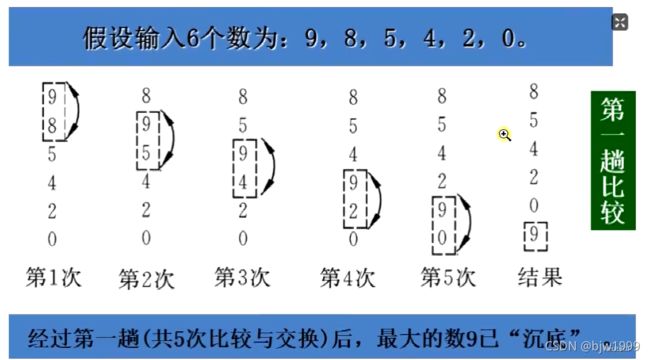
1、冒泡排序

算法思路

• 比较相邻的元素,如果第一个比第二个大,就交换他们两个;
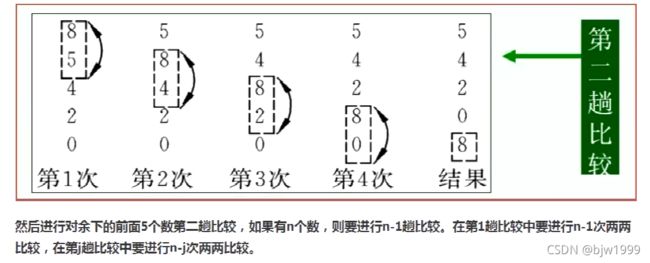
• 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样一轮比较完最后的元素应该会是最大的数;
• 针对所有的元素重复以上的步骤,除了最后一个;
• 重复步骤1~3,直到排序完成。
• 
• 

 代码实现过程：

public static int[] sort(int[] a) {
    for (int i = 1; i < a.length; i++) {           //外循环为比较几趟
        for (int j = 0; j < a.length - i; j++) {   
            if (a[j] > a[j + 1]) {
                int temp = a[j + 1];
                a[j + 1] = a[j];
                a[j] = temp;
            }
        }
    }
    return a;
}

算法稳定性:

如果待排序的序列中存在两个或两个以上具有相同关键词的数据,排序后这些数据的相对次序保持不变,通俗地讲,就是两个相同的数的相对顺序不会发生改变,则该算法是稳定;冒泡排序是稳定的排序算法。

时间复杂度：

对于n位的数列则有比较次数为（n-1）+（n+2）+ . . . + 1 = n * (n-1) / 2,这就得到了最大的比较次数,n(n-1)/2 = (-n) / 2,计算时间复杂度的时候,忽略常数项1/2,在忽略低阶项n,得到冒泡排序的时间复杂度为O()

2、选择排序

选择排序是一种简单直观的排序算法。

算法思路：

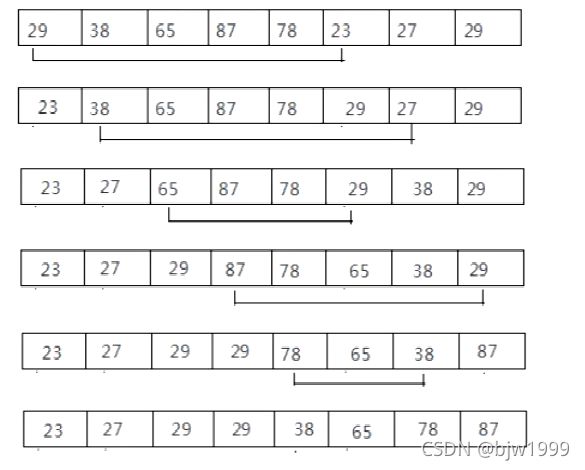
以由小到大排序为例，首先在未排序序列中找到最小元素，存放到排序序列的起始位置，然后再从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾。以此类推，直到所有元素均排序完毕。 

 第一轮：找到最小值23，跟第1个位置29交换，得到有序集合{23}。

 第二轮：从无序集合中找到最小值27，跟第2个位置38交换，得到有序集合{23，27}。

以此类推，总共比较n-1趟。

代码实现：

public static void chooseSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[i] > arr[j]) {        //无序集合中的第一个只要比后面的某个数大就交换
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
    }
}

算法稳定性:

选择排序时不稳定的算法。例如序列“5(1) ,8 ,5(2) ,2 ,9”,5(1)会和2交换,相对位置在5(2)的后面了,所以破坏稳定性。

时间复杂度：

• n-1
• n-2
• n-3
• n-4
• n-1:1  比较次数:(n-1+1)(n-1)/2=(n^2-n)/2   时间复杂度=O()

3、快速排序

快速排序(Quicksort)是对冒泡排序算法的一种改进。

算法思路：

快速排序算法的排序流程如下：

• 先从数列中取出一个数作为基准数。
• 分区过程，将比这个数大的数全放到它的右边，小于或等于它的数全放到它的左边。
• 再对左右区间重复第二步，直到各区间只有一个数。(递归)

 经过第一趟排序,数组被划分为两个区,5左边是小于5的{2,3,0,1,4}，5右边是大于5的{6,7,9,10,8}。我们在分别对这两个区进行递归操作，直至每个组只剩下1个数字，排序完成！

代码实现:

public static void quickSort(int[] a, int low, int high) {
    if (low >= high) {
        return;
    }

    int i = low;
    int j = high;
    int base = a[i];
    while (i < j) {
                //先进行从后往前比较,比基准值小的交换,否则一直往前找比基准值小的
        while (a[j] >= base && i < j) {
            j--;
        }
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
                //从前往后比较，找比基准值大的交换，否则一直往后找
        while (a[i] <= base && i < j) {
            i++;
        }
        temp = a[i];
        a[i] = a[j];
        a[j] = temp;

    }
        //当i=j时,就以i或者j下标的元素看成分界线,这时左边比这个分界线的数小,右边比这个分界线的值大。然后再对这两个区进行递归，直到每个组只剩一个数
    quickSort(a, low, i - 1);   //分界线左边进行排序
    quickSort(a, i + 1, high);  //分界线后边进行排序
}

排序稳定性：

快速排序排序是不稳定的排序算法。

时间复杂度: 

4、插入排序

插入排序时一种简单直观的排序算法。

算法思路：

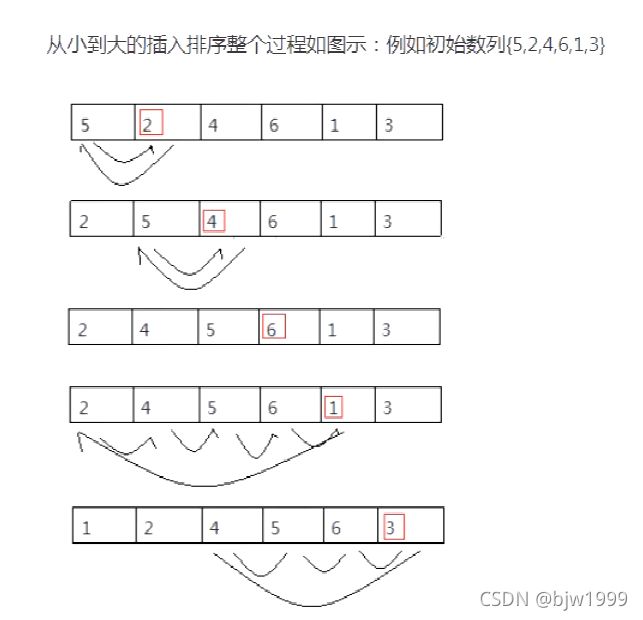
把n个待排序的元素看成为一个有序表和一个无序表，开始时有序表中只包含1个元素，无序表中包含有n-1个元素，排序过程中每次从无序表中取出第一个元素，将它插入到有序表中的适当位置，使之成为新的有序表，重复n-1次可完成排序过程。

第一轮：从第二个位置的2开始比较，比前面5小，交换位置。

第二轮：这时有序表为2和5，无序表为4、6、1、3，然后继续无序表中的第一个数在有序表中从后往前比较，直到比它大才停止比较。以此类推。。。

代码实现：

public static void insertSort(int[] arr) {
    for (int i = 1; i < arr.length; i++) {  //比较的趟数
        for (int j = i; j > 0; j--) {       
            if (arr[j] < arr[j - 1]) {      //找如果比有序表中的数小就交换,否则停止插入
                int temp = arr[j];
                arr[j] = arr[j - 1];
                arr[j - 1] = temp;
            } else {
                break;
            }
        }
    }
}

算法稳定性:

插入排序是稳定的排序算法。

时间复杂度：

O(n^2)

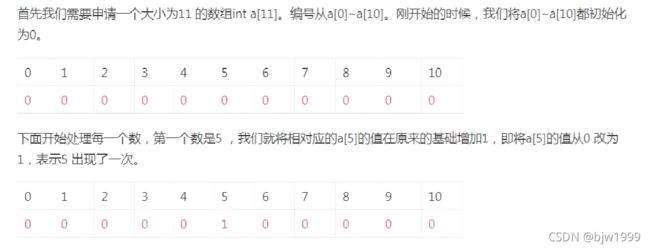
5、计数排序

计数排序是一种非比较排序算法，其核心在于将输入的数据值转换为键存储在额外开辟的数组空间中，作为一种线性时间复杂度的排序，计数排序需要输入的数据必须是有确定范围的整数。

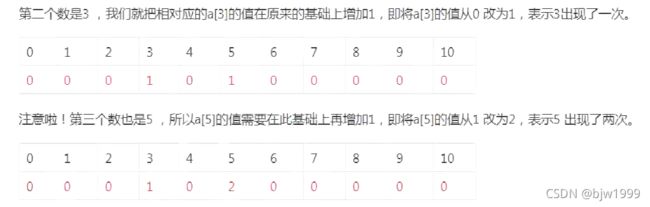
    原始序列为：5 ,3 ,5 ,8 ,2 ,10

 代码实现：

public static void countSort(int[] arr) {
    //找出最大的数max
    int max = arr[0];
    for (int i = 1; i < arr.length; i++) {
        if (arr[i] > max) {
            max = arr[i];
        }
    }
    //找出最小的数min
    int min = arr[0];
    for (int i = 1; i < arr.length; i++) {
        if (arr[i] < min) {
            min = arr[i];
        }
    }
    //创建计数数组
    int[] count = new int[max + 1];
    //遍历arr
    for (int i = 0; i < arr.length; i++) {
        count[arr[i]]++;
    }
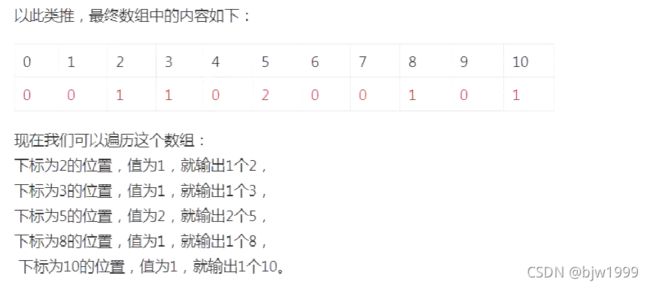
    //遍历输出计数数组
    int k = 0;
    for (int i = 0; i < count.length; i++) {
        while (count[i] > 0) {
            arr[k++] = i;
            count[i]--;
        }
    }
}

代码优化：

我们考虑一个问题，如果数组是[101,103,110,116,,119,120],如果开辟了一个121大小的数组,前100个位置都是空的,显然是不合适的,因此我们可以把数组的大小设置成max-min+1。这时，我们向数组中计数时，下标要减去一个偏移量min，输出数组的时候，要加上这个偏移量。

算法稳定性：

计数排序是一个稳定排序算法。

时间复杂度：

时间复杂度是O(n+k)，其中n是数组长度，k是数据的范围，因为将n个数放入计数数组的时间复杂度是O(n)，从长度为k的计数数组中输出元素的时间复杂度为O(k)，所以总的时间复杂度为O(n+k).

6、希尔排序

7、堆排序

8、归并排序

9、桶排序

10、基数排序