朴素贝叶斯分类器之分类实操

python 朴素贝叶斯分类器之分类实操

基本概念

鲁棒性

Huber从稳健统计的角度系统地给出了鲁棒性3个层面的概念：

1.是模型具有较高的精度或有效性，这也是对于机器学习中所有学习模型的基本要求；
2.是对于模型假设出现的较小偏差，只能对算法性能产生较小的影响，如噪声；
3.是对于模型假设出现的较大偏差，不可对算法性能产生“灾难性”的影响，如离群点。

PS：上面的解释是从网上抄来的

定义：对于聚类（分类）算法而言，鲁棒性意味着聚类结果不应受到模型中存在的数据扰动、噪声及离群点的太大影响。

算法简介

朴素贝叶斯分类器

朴素贝叶斯分类器是与之前提到的逻辑算法（LogisticRegression)等线性模型非常相似的一种分类器，但它的训练速度往往更快。它通过单独查看每个特征来学习参数，并从每个特征中收集简单的类别统计数据。

python的第三方库scikit-learn中实现了三种朴素贝叶斯分类器：
GaussianNB（高斯分类器）:可应用于任意连续数据。
BernoulliNB（伯努利分类器）:假定输入数据为二分类数据。
MultinomialNB（多项式分类器）:假定输入数据为计数数据（即每个特征代表某个对象的整数计数）。

GaussianNB主要用于高维度数据，而另外两种朴素贝叶斯分类模型则广泛用于稀疏计数数据，比如文本。

MultinomialNB与GaussianNB计算的统计数据类型略有不同。MultinomialNB计算每个类别中每个特征的平均值，而GaussianNB会保存每个类别中每个特征的平均值和标准差。

对于朴素贝叶斯分类器来说，要想作出预测，需要将数据点与每个类别的统计数据做比较，并将最匹配的类别作为预测结果。有意思的是，MultinomialNB与BernoulliNB预测公式的形式都与线性模型完全相同。

本文主要介绍伯努利和多项式分类器，而高斯分类器的用法可以类比之前的其它线性算法，如lasso，ridge等。

数据来源

蘑菇的可食用性分类：https://www.kaggle.com/uciml/mushroom-classification

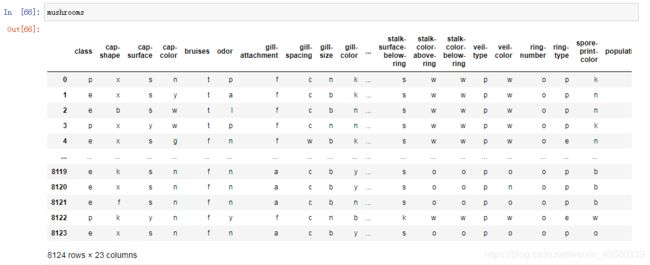
该集合以文本的形式记录了多种蘑菇的菌盖，菌柄，菌丝等部位的颜色，宽度，长度数据。
数据集一共有8124条特征记录，22个特征维度，并对这些蘑菇划分成两类（class）：e——可食用；p——有毒的。

数据挖掘

1.导入第三方库并读取文件

import pandas as pd
import numpy as np
import winreg
from sklearn.model_selection import train_test_split
from sklearn.naive_bayes import BernoulliNB#伯努利贝叶斯分类器
from sklearn.metrics import accuracy_score
###################
real_address = winreg.OpenKey(winreg.HKEY_CURRENT_USER,r'Software\Microsoft\Windows\CurrentVersion\Explorer\Shell Folders',)
file_address=winreg.QueryValueEx(real_address, "Desktop")[0]
file_address+='\\'
file_origin=file_address+"\\源数据-分析\\mushrooms.csv"
mushrooms=pd.read_csv(file_origin)
#设立桌面绝对路径，读取源数据文件，这样将数据直接下载到桌面上就可以了，省得还要去找
###################

老规矩，上来先依次导入建模需要的各个模块，并读取文件。

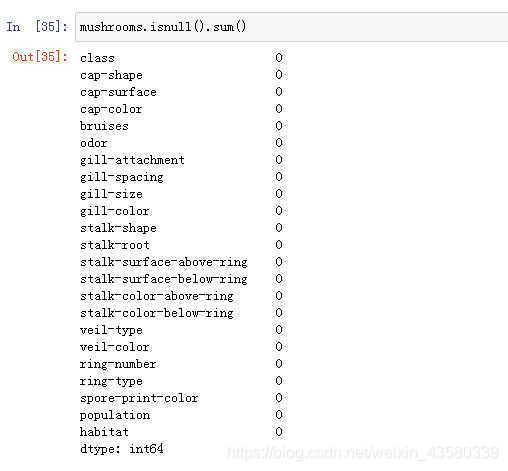
2.清洗数据

查找缺失值：

从上面的结果来看，数据中没有缺失值。

3.建模

首先将待测的分类特征（有毒与可食用）划分出来。

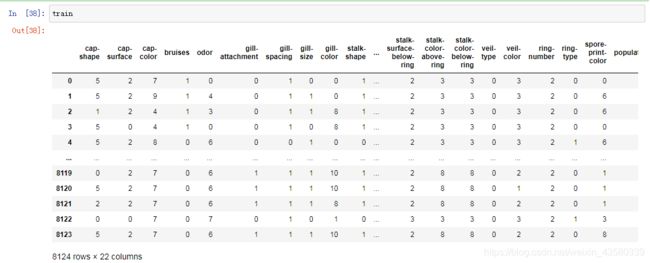
train=mushrooms.drop(["class"],axis=1)

由于这个数据是以文本的形式记录的，直接建模的话，算法会识别不出来，所以需要把其中的文本数据依次替换成数字，如特征维度菌盖（cap-color）包含十种颜色，将这十种颜色分别以数字0-9替换表示，代码如下所示：

for i in train.columns:
    a=list(set(train[i]))###set是获得去重元素值
    for m in range(len(a)):
        train[i].loc[train[i]==a[m]]=m

替换后结果如下所示：

接下来，划分列索引为特征值和预测值，并将数据划分成训练集和测试集：

X_train,X_test,y_train,y_test=train_test_split(train,mushrooms["class"],random_state=1)

引入伯努利算法，并将算法中的参数依次设立好，进行建模后，对测试集进行精度评分：

import time###引入时间模块，接下来的讨论会用到
start=time.time()
clf=BernoulliNB(alpha=10)
train_prediction=clf.fit(X_train,y_train).predict(X_train)
test_prediction=clf.fit(X_train,y_train).predict(X_test)
print("伯努利贝叶斯训练模型评分："+str(accuracy_score(y_train,train_prediction)))
print("伯努利贝叶斯待测模型评分："+str(accuracy_score(y_test,test_prediction)))
end=time.time()
print ("运行时间："+str(end-start))#时间单位是秒

得到的结果如下：

可以看到，该模型的精度为90%左右，运行时间是0.14s。

4.参数

MultinomialNB与BernoulliNB都只有一个参数alpha，用于控制模型复杂度。

alpha的工作原理：算法向数据中添加alpha这么多的虚拟数据点，这些点对所有特征都取正值。这可以将统计数据“平滑化”。alpha越大，平滑化就越强，模型复杂度就越低。

朴素贝叶斯分类器的算法性能对alpha值的鲁棒性相对较好，也就是说，alpha值对模型性能并不重要，但调用这参数通常都会使精度略有提高。
接下来，我们看一下模型精度与alpha之间的关系，代码如下所示：

from sklearn.naive_bayes import MultinomialNB#多项式贝叶斯分类器
result=pd.DataFrame(columns=["参数","伯努利训练模型得分","伯努利待测模型得分","多项式训练模型得分","多项式待测模型得分"])
for i in range(1,300):
    Bernoulli=BernoulliNB(alpha=i).fit(X_train,y_train)
    Multinomial=MultinomialNB(alpha=i).fit(X_train,y_train)
    result=result.append([{"参数":i,"伯努利训练模型得分":accuracy_score(y_train,Bernoulli.predict(X_train)),"伯努利待测模型得分":accuracy_score(y_test,Bernoulli.predict(X_test)),"多项式训练模型得分":accuracy_score(y_train,Multinomial.predict(X_train)),"多项式待测模型得分":accuracy_score(y_test,Multinomial.predict(X_test))}])

以折线图的形式展现出来：

import matplotlib.pyplot as plt
import seaborn as sns
plt.style.use("fivethirtyeight")
sns.set_style({'font.sans-serif':['SimHei','Arial']})#设定汉字字体，防止出现方框
%matplotlib inline
#在jupyter notebook上直接显示图表
fig= plt.subplots(figsize=(15,5))
plt.plot(result["参数"],result["伯努利训练模型得分"],label="伯努利训练模型得分")#画折线图
plt.plot(result["参数"],result["伯努利待测模型得分"],label="伯努利待测模型得分")
plt.plot(result["参数"],result["多项式训练模型得分"],label="多项式训练模型得分")
plt.plot(result["参数"],result["多项式待测模型得分"],label="多项式待测模型得分")
plt.rcParams.update({'font.size': 15})
plt.legend()
plt.xticks(fontsize=15)#设置坐标轴上的刻度字体大小
plt.yticks(fontsize=15)
plt.xlabel("参数",fontsize=15)#设置坐标轴上的标签内容和字体
plt.ylabel("得分",fontsize=15)

结果如下所示：

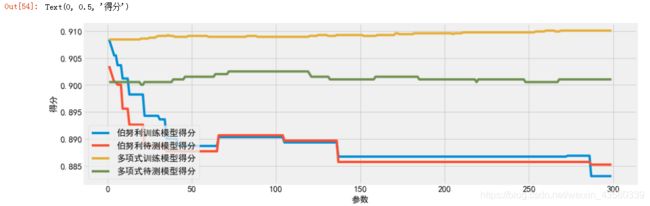
从图中可以看出MultinomialNB（多项式）比BernoulliNB（伯努利）的性能和稳定性要好很多，而对于BernoulliNB来说，模型性能会随着alpha的增加而逐渐下降。

小结

朴素贝叶斯模型的许多优点和缺点都与线性模型相同。它的训练和预测速度都很快，训练过程也很容易理解。但这种高效率所付出的代价就是，朴素贝叶斯模型的泛化能力要比线性分类器（如逻辑算法（LogisticRegression)）稍差。
接下来，用线性模型LogisticRegression算法来建模，与朴素贝叶斯做个比较，代码如下：

from sklearn.linear_model import LogisticRegression
start=time.time()
logistic=LogisticRegression(penalty='l2',C=1,solver='lbfgs',max_iter=1000)
train_prediction=logistic.fit(X_train,y_train).predict(X_train)
test_prediction=logistic.fit(X_train,y_train).predict(X_test)
print("Logistic训练模型评分："+str(accuracy_score(y_train,train_prediction)))
print("Logistic待测模型评分："+str(accuracy_score(y_test,test_prediction)))
end=time.time()
print ("运行时间："+str(end-start))

结果如下：

从上面结果可以看出，对于同样的数据，逻辑算法的模型精度要优于朴素贝叶斯算法，但是运行时间是0.96秒，比朴素贝叶斯的运行时间要多了7倍左右，而随着数据量达到万级，甚至继续增加，这个差距会越来越大。

总的来说，朴素贝叶斯分类器对高维稀疏数据的效果很好，对参数的鲁棒性也相对较好，是很好的基准模型，可用于非常大的数据集，毕竟在这些数据集上即使训练线性模型可能也要花费大量的时间。

个人博客：https://www.yyb705.com/
欢迎大家来我的个人博客逛一逛，里面不仅有技术文，也有系列书籍的内化笔记。
有很多地方做的不是很好，欢迎网友来提出建议，也希望可以遇到些朋友来一起交流讨论。