强化学习-学习笔记14 | 策略梯度中的 Baseline

优质资源分享

学习路线指引（点击解锁）	知识定位	人群定位
Python实战微信订餐小程序	进阶级	本课程是python flask+微信小程序的完美结合，从项目搭建到腾讯云部署上线，打造一个全栈订餐系统。
Python量化交易实战	入门级	手把手带你打造一个易扩展、更安全、效率更高的量化交易系统

本篇笔记记录学习在 策略学习 中使用 Baseline，这样可以降低方差，让收敛更快。

14. 策略学习中的 Baseline

14.1 Baseline 推导

• 在策略学习中，我们使用策略网络 π(a|s;θ)\pi(a|s;\theta) 控制 agent，
• 状态价值函数

Vπ(s)=EA∼π[Qπ(s,A)]=∑aπ(a|s;θ)⋅Qπ(a,s)V_\pi(s)=\mathbb{E}_{A\sim \pi}[Q_\pi(s,A)]=\sum\limits_{a}\pi(a|s;\theta)\cdot Q_\pi(a,s)

• 策略梯度：

∂ Vπ(s)∂ θ=EA∼π[∂lnπ(A|s;θ)∂θ⋅Qπ(s,A)]\frac{\partial \ V_\pi(s)}{\partial \ \theta}=\mathbb{E}_{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot Q_\pi(s,A)]

在策略梯度算法中引入 Baseline 主要是用于减小方差，从而加速收敛

Baseline 可以是任何 独立于 动作 A 的数，记为 b。

Baseline的性质：

• 这个期望是0： EA∼π[b⋅∂ lnπ(A|s;θ)∂θ]=0\mathbb{E}_{A\sim\pi}[b\cdot \frac{\partial \ \ln\pi(A|s;\theta)}{\partial\theta}]=0

  • 因为 b 不依赖 动作 A ，而该式是对 A 求期望，所以可以把 b 提出来，有：b⋅EA∼π[∂ lnπ(A|s;θ)∂θ]b\cdot \mathbb{E}_{A\sim\pi}[\frac{\partial \ \ln\pi(A|s;\theta)}{\partial\theta}]
  • 而期望 E 这一项可以展开：b∑aπ(a|s;θ)⋅∂lnπ(A|s;θ)∂θb\sum_a \pi(a|s;\theta)\cdot\frac{\partial\ln_\pi(A|s;\theta)}{\partial\theta}

  这个性质在策略梯度算法用到的的两种形式有提到过。

  • 用链式法则展开后面的导数项，即: ∂lnπ(A|s;θ)∂θ=1π(a|s;θ)⋅∂π(a|s;θ)∂θ\frac{\partial\ln_\pi(A|s;\theta)}{\partial\theta}={\frac{1}{\pi(a|s;\theta)}\cdot \frac{\partial\pi(a|s;\theta)}{\partial\theta}}
  • 这样整个式子为：b∑aπ(a|s;θ)⋅1π(a|s;θ)⋅∂π(a|s;θ)∂θ=b⋅∑a∂π(a|s;θ)∂θb\sum_a \pi(a|s;\theta)\cdot{\frac{1}{\pi(a|s;\theta)}\cdot \frac{\partial\pi(a|s;\theta)}{\partial\theta}}=b\cdot \sum_a\frac{\partial\pi(a|s;\theta)}{\partial\theta}
  • 由于连加是对于 a 进行连加，而内部求导是对于 θ 进行求导，所以求和符号可以和导数符号交换位置：

  b⋅∂∑aπ(a|s;θ)∂θb\cdot \frac{\partial\sum_a\pi(a|s;\theta)}{\partial\theta}

  这是数学分析中 级数部分 的内容。

  • 而 ∑aπ(a|s;θ)=1\sum_a\pi(a|s;\theta)=1，所以有b⋅∂1∂θ=0b\cdot \frac{\partial 1}{\partial \theta}=0

根据上面这个式子的性质，可以向 策略梯度中添加 baseline

• 策略梯度 with baseline：KaTeX parse error: Can't use function '\=' in math mode at position 223: …artial\theta}] \̲=̲\mathbb{E}*{A\s…
• 这样引入b对期望 E\mathbb{E} 没有影响，为什么要引入 b 呢？
  • 策略梯度算法中使用的并不是 严格的上述式子，而是它的蒙特卡洛近似；
  • b不影响期望，但是影响蒙特卡洛近似；
  • 如果 b 好，接近 QπQ_\pi，那么会让蒙特卡洛近似的方差更小，收敛速度更快。

14.2 策略梯度的蒙特卡洛近似

上面我们得到：∂ Vπ(st)∂ θ=EAt∼π[∂lnπ(At|st;θ)∂θ⋅(Qπ(st,At)−b)]\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}=\mathbb{E}_{A_t\sim\pi}[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-b)]

但直接求期望往往很困难，通常用蒙特卡洛近似期望。

• 令 g(At)=[∂lnπ(At|st;θ)∂θ⋅(Qπ(st,At)−b)]g(A_t)=[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-b)]
• 根据策略函数 π\pi 随机抽样 ata_t ，计算 g(at)g(a_t)，这就是上面期望的蒙特卡洛近似；g(at)=[∂lnπ(at|st;θ)∂θ⋅(Qπ(st,at)−b)]g(a_t)=[\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,a_t)-b)]
• g(at)g(a_t) 是对策略梯度的无偏估计；

因为：EAt∼π[g(At)]=∂Vπ(st)∂θ\mathbb{E}_{A_t\sim\pi}[g(A_t)]=\frac{\partial V_\pi(s_t)}{\partial\theta}，期望相等。

• g(at)g(a_t) 是个随机梯度，是对策略梯度 EAt∼π[g(At)]\mathbb{E}_{A_t\sim\pi}[g(A_t)]的蒙特卡洛近似

• 在实际训练策略网络的时候，用随机梯度上升更新参数θ：θ←θ+β⋅g(at)\theta \leftarrow \theta+\beta\cdot g(a_t)

• 策略梯度是 g(at)g(a_t) 的期望，不论 b 是什么，只要与 A 无关，就都不会影响 g(At)g(A_t) 的期望。为什么不影响已经在 14.1 中讲过了。

  • 但是 b 会影响 g(at)g(a_t)；
  • 如果 b 选取的很好，很接近 QπQ_\pi，那么随机策略梯度g(at)g(a_t)的方差就会小；

14.3 Baseline的选取

介绍两种常用的 baseline。

回到顶部#### a. b=0

第一种就是把 baseline 取0，即与之前相同：∂ Vπ(s)∂ θ=EA∼π[∂lnπ(A|s;θ)∂θ⋅Qπ(s,A)]\frac{\partial \ V_\pi(s)}{\partial \ \theta}=\mathbb{E}_{A\sim\pi}[\frac{\partial ln \pi(A|s;\theta)}{\partial \theta}\cdot Q_\pi(s,A)]

回到顶部#### b. b= VπV_\pi

另一种就是取 b 为 VπV_\pi，而 VπV_\pi 只依赖于当前状态 sts_t，所以可以用来作为 b。并且 VπV_\pi 很接近 QπQ_\pi，可以降低方差加速收敛。

因为 Vπ(st)=E[Qπ(st,At)]V_\pi(s_t)=\mathbb{E}[Q_\pi(s_t,A_t)]，作为期望，V 很接近 Q。

14.4 Reinforce with Baseline

把 baseline 用于 Reinforce 算法上。

回到顶部#### a. 基本概念

• 折扣回报：Ut=Rt+γ⋅Rt+1+γ2⋅Rt+2+…U_t=R_t+\gamma\cdot R_{t+1}+\gamma^2\cdot R_{t+2}+…
• 动作价值函数：Qπ(st,at)=E[Ut|st,at].Q_\pi(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t].
• 状态价值函数：Vπ(st)=EA[Qπ(st,A)|st]V_\pi(s_t)=\mathbb{E}_A[Q_\pi(s_t,A)|s_t]
• 应用 baseline 的策略梯度：使用的是上面第二种 baseline：

∂ Vπ(st)∂ θ=EAt∼π[g(At)]=EAt∼π[∂lnπ(At|st;θ)∂θ⋅(Qπ(st,At)−Vπ(st))]\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}=\mathbb{E}_{A_t\sim\pi}[g(A_t)]=\mathbb{E}_{A_t\sim\pi}[\frac{\partial ln \pi(A_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,A_t)-V_\pi(s_t))]

• 对动作进行抽样，用 g(at)g(a_t) 做蒙特卡洛近似，为无偏估计（因为期望==策略梯度）：at∼π(⋅|st;θ)a_t\sim\pi(\cdot|s_t;\theta)

g(at)g(a_t) 就叫做 随机策略梯度，用随机抽取的动作 对应的值来代替期望，是策略梯度的随即近似；这正是**蒙特卡洛方法**的应用。

+ g(at)=[∂lnπ(at|st;θ)∂θ⋅(Qπ(st,at)−b)]g(a\_t)=[\frac{\partial ln \pi(a\_t|s\_t;\theta)}{\partial \theta}\cdot(Q\_\pi(s\_t,a\_t)-b)]

但上述公式中还是有不确定的项:Qπ  VπQ_\pi \ \ V_\pi，继续近似：

• 用观测到的 utu_t 近似 QπQ_\pi，因为 Qπ(st,at)=E[Ut|st,at].Q_\pi(s_t,a_t)=\mathbb{E}[U_t|s_t,a_t].这也是一次蒙特卡洛近似。

这也是 Reinforce 算法的关键。

• 用神经网络-价值网络 v(s;w)v(s;w) 近似 VπV_\pi；

所以最终近似出来的 策略梯度 是：

∂ Vπ(st)∂ θ≈g(at)≈∂lnπ(at|st;θ)∂θ⋅(ut−v(s;w))\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}\approx g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(u_t-v(s;w))
当我们知道 策略网络π\pi、折扣回报utu_t 以及 价值网络vv，就可以计算这个策略梯度。

我们总计做了3次近似：

1. 用一个抽样动作 ata_t 带入 g(at)g(a_t) 来近似期望；
2. 用回报 utu_t 近似动作价值函数QπQ_\pi；

1、2都是蒙特卡洛近似；

3. 用神经网络近似状态价值函数VπV_\pi

函数近似。

回到顶部#### b. 算法过程

我们需要建立一个策略网络和一个价值网络，后者辅助训练前者。

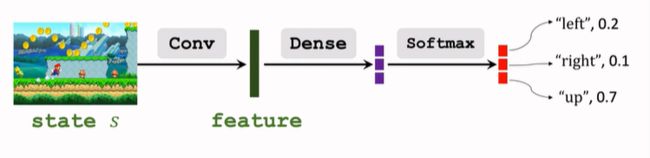
• 策略网络：

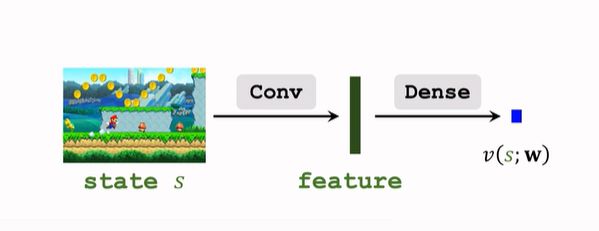
• 价值网络：

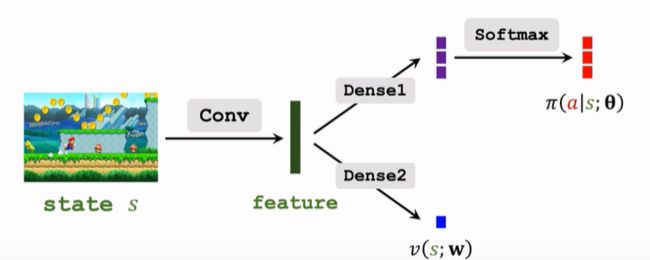
• 参数共享：

用 Reinforce 算法训练策略网络，用回归方法训练价值网络。

• 在一次训练中 agent 获得轨迹：s1,a1,r1,s2,a2,r2,…s_1,a_1,r_1,s_2,a_2,r_2,…

• 计算 ut=∑ni=tγi−triu_t=\sum_{i=t}^n\gamma{i-t}r^i

• 更新策略网络

  1. 得到策略梯度：∂ Vπ(st)∂ θ≈∂lnπ(at|st;θ)∂θ⋅(ut−v(s;w))\frac{\partial \ V_\pi(s_t)}{\partial \ \theta}\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(u_t-v(s;w))
  2. 梯度上升，更新参数：θ←θ+β⋅∂lnπ(at|st;θ)∂θ⋅(ut−v(st;w))\theta\leftarrow \theta + \beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial\theta}\cdot(u_t-v(s_t;w))

  记 ut−v(st;w)u_t-v(s_t;w) 为 −δt-\delta_t

  θ←θ−β⋅∂lnπ(at|st;θ)∂θ⋅δt\theta\leftarrow \theta - \beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial\theta}\cdot \delta_t

• 更新价值网络

回顾一下价值网络的目标：VπV_\pi 是 UtU_t 的期望，训练价值网络是让v接近期望 VπV_\pi

1. 用观测到的 utu\_t 拟合 v，两者之间的误差记为


prediction error:δt=v(st;w)−ut\delta\_t=v(s\_t;w)-u\_t，
2. 求导得策略梯度: ∂δ2/2∂w=δt⋅∂v(st;w)∂w\frac{\partial \delta^2/2}{\partial w}=\delta\_t\cdot \frac{\partial v(s\_t;w)}{\partial w}
3. 梯度下降更新参数：w←w−α⋅δt⋅∂v(st;w)∂ww\leftarrow w-\alpha\cdot\delta\_t\cdot\frac{\partial v(s\_t;w)}{\partial w}

• 如果轨迹的长度为n，可以对神经网络进行n次更新

14.5 A2C算法

回到顶部#### a.基本概念

Advantage Actor Critic. 把 baseline 用于 Actor-Critic 上。

所以需要一个策略网络 actor 和一个价值网络 critic。但与 第四篇笔记AC算法有所不同。

• 策略网络还是 π(a|s;θ)\pi(a|s;\theta)，而价值网络是 v(s;w)v(s;w)，是对VπV_\pi 的近似，而不是第四篇笔记中的 QπQ_\pi。

因为 V 不依赖于动作，而 Q 依赖动作和状态，故 近似V 的方法可以引入 baseline。

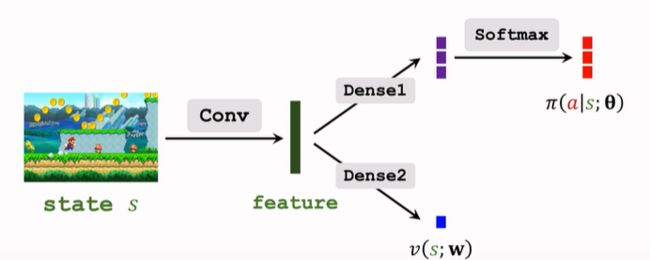
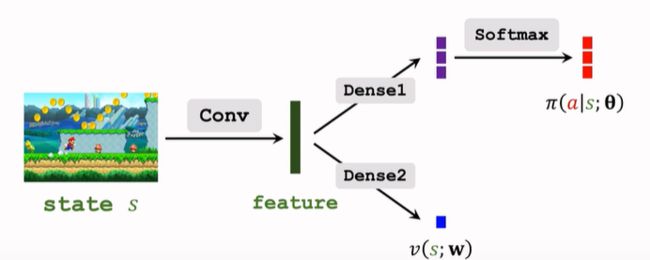
• A2C 网络结构：

与 14.4 中的结构相同，区别在于训练方法不同。

回到顶部#### b. 训练过程

1. 观察到一个 transition(st，at,rt,st+1s_t，a_t,r_t,s_{t+1})
2. 计算 TD target：yt=rt+γ⋅v(st+1;w)y_t=r_t+\gamma\cdot v(s_{t+1};w)
3. 计算 TD error：δt=v(st;w)−yt\delta_t=v(s_t;w)-y_t
4. 用策略网络梯度更新策略网络θ：θ←θ−β⋅δt⋅∂lnπ(at|st;θ)∂θ\theta\leftarrow \theta-\beta\cdot\delta_t\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial \theta}

注意！这里的 δt\delta_t​ 是前文中的 “ut−v(st;w)u_t-v(s_t;w) 为 −δt-\delta_t”

5. 用TD更新价值网络：w←w−α⋅δt⋅∂v(st;w)∂ww\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}

回到顶部#### c. 数学推导

A2C的基本过程就在上面，很简洁，下面进行数学推导。

1.价值函数的性质

• QπQ_\pi

  • TD算法推导时用到过这个式子：Qπ(st,at)=ESt+1,At+1[Rt+γ⋅Qπ(St+1,At+1)]Q_\pi(s_t,a_t)=\mathbb{E}_{S_{t+1},A_{t+1}}[R_t+\gamma\cdot Q_\pi(S_{t+1},A_{t+1})]
  • 随机性来自 St+1,At+1S_{t+1},A_{t+1}，而对之求期望正好消掉了随机性，可以把对 At+1A_{t+1} 的期望放入括号内，RtR_t 与 At+1A_{t+1} 无关，则有 定理一：

  Qπ(st,at)=ESt+1[Rt+γ⋅EAt+1[Qπ(St+1,At+1)]=ESt+1[Rt+γ⋅Vπ(st+1)]Q_\pi(s_t,a_t)= \mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot \mathbb{E}_{A_{t+1}}[Q_\pi(S_{t+1},A_{t+1})]\=\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(s_{t+1})]

  • 即：Qπ(st,at)=ESt+1[Rt+γ⋅Vπ(st+1)]Q_\pi(s_t,a_t)=\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(s_{t+1})]

• VπV_\pi

  • 根据定义： Vπ(st)=E[Qπ(st,At)]V_\pi(s_t)=\mathbb{E}[Q_\pi(s_t,A_t)]
  • 将 Q 用 定理一 替换掉：

  Vπ(st)=EAtESt+1[Rt+γ⋅Vπ(St+1)]=EAt,St+1[Rt+γ⋅Vπ(St+1)]V_\pi(s_t)=\mathbb{E}_{A_t}\mathbb{E}_{S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})]\=\mathbb{E}_{A_t,S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})]

  • 这就是 定理二：Vπ(st)=EAt,St+1[Rt+γ⋅Vπ(St+1)]V_\pi(s_t)=\mathbb{E}_{A_t,S_{t+1}}[R_t+\gamma\cdot V_\pi(S_{t+1})]

这样就将 Q 和 V 表示为期望的形式，A2C会用到这两个期望，期望不好求，我们是用蒙特卡洛来近似求期望：

• 观测到 transition(st,at,rt,st+1s_t,a_t,r_t,s_{t+1})

• QπQ_\pi

  • Qπ(st,at)≈rt+γ⋅Vπ(st+1)Q_\pi(s_t,a_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})
  • 训练策略网络；

• VπV_\pi

  • Vπ(st)≈rt+γ⋅Vπ(st+1)V_\pi(s_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})
  • 训练价值网络，这也是TD target 的来源；

2. 更新策略网络

即使用 baseline 的策略梯度算法。

• g(at)=[∂lnπ(at|st;θ)∂θ⋅(Qπ(st,at)−Vπ(st))]g(a_t)=[\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot(Q_\pi(s_t,a_t)-V_\pi(s_t))] 是策略梯度的蒙特卡洛近似。
• 前面Dueling Network提到过，Qπ−VπQ_\pi-V_\pi是优势函数 Advantage Function.

这也是 A2C 的名字来源。

• Q 和 V 都还不知道，需要做近似，14.5.c.1 中介绍了：

  • Qπ(st,at)≈rt+γ⋅Vπ(st+1)Q_\pi(s_t,a_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})
  • 所以是：g(at)≈∂lnπ(at|st;θ)∂θ⋅[(rt+γ⋅Vπ(st+1))−Vπ(st)]g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot V_\pi(s_{t+1}))-V_\pi(s_t)]
  • 对 VπV_\pi 进行函数近似 v(s;w)v(s;w)
  • 则得最终：g(at)≈∂lnπ(at|st;θ)∂θ⋅[(rt+γ⋅v(st+1;w))−v(st;w)]g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot v(s_{t+1;w}))-v(s_{t;w})]用上式更新策略网络。

• 而 rt+γ⋅v(st+1;w)r_t+\gamma\cdot v(s_{t+1;w}) 正是 TD target yty_t

• 梯度上升更新参数：θ←θ−β⋅∂lnπ(at|st;θ)∂θ⋅(yt−v(st;w))\theta\leftarrow \theta-\beta\cdot\frac{\partial\ln\pi(a_t|s_t;\theta)}{\partial \theta}\cdot (y_t-v(s_t;w))

这样的梯度上升更好。

因为以上式子中都有 V，所以需要近似计算 V：

g(at)≈∂lnπ(at|st;θ)∂θ⋅[(rt+γ⋅Vπ(st+1))−Vπ(st)]⏟evaluation made by the criticg(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot\underbrace{[(r_t+\gamma\cdot V_\pi(s_{t+1}))-V_\pi(s_t)]}_{evaluation \ made \ by \ the \ critic}

3. 更新价值网络

采用 TD 算法 更新价值网络，根据 14.5.b 有如下式子：

• Vπ(st)≈rt+γ⋅Vπ(st+1)V_\pi(s_t)\approx r_t+\gamma\cdot V_\pi(s_{t+1})
• 对上式得 VπV_\pi 做函数近似， 替换为 v(st;w),v(st+1;w)v(s_t;w),v(s_{t+1;w})；
• v(st;w)≈rt+γ⋅v(st+1;w)⏟TD target ytv(s_t;w)\approx \underbrace{r_t+\gamma\cdot v(s_{t+1};w)}_{TD \ target \ y_t}
• 训练价值网络就是要让 v(s;w)v(s;w) 接近 yty_t
  • TD error: δt=v(st;w)−yt\delta_t=v(s_t;w)-y_t
  • 梯度: ∂δ2t/2∂w=δt⋅∂v(st;w)∂w\frac{\partial\delta^2_t/2}{\partial w}=\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}
  • 更新：w←w−α⋅δt⋅∂v(st;w)∂ww\leftarrow w-\alpha\cdot\delta_t\cdot\frac{\partial v(s_t;w)}{\partial w}

4. 有关的策略梯度

在A2C 算法中的策略梯度：g(at)≈∂lnπ(at|st;θ)∂θ⋅[(rt+γ⋅v(st+1;w))−v(st;w)]g(a_t)\approx\frac{\partial ln \pi(a_t|s_t;\theta)}{\partial \theta}\cdot[(r_t+\gamma\cdot v(s_{t+1;w}))-v(s_{t;w})]

会有这么一个问题，后面这一项是由价值网络给出对策略网络选出的动作进行打分，那么为什么这一项中没有动作呢，没有动作怎么给动作打分呢？

• 注意这两项：
• (rt+γ⋅v(st+1;w))(r_t+\gamma\cdot v(s_{t+1;w})) 是执行完 ata_t 后作出的预测
• v(st;w)v(s_t;w) 是未执行 ata_t 时作出的预测；
• 两者之差意味着动作 ata_t 对于 V 的影响程度
• 而在AC算法中，价值网络给策略网络的是 q，而在A2C算法中， 价值网络给策略网络的就是上两式之差 advantage.

14.6 RwB 与A2C 的对比

• 两者的神经网络结构完全一样

• 不同的是价值网络

  • RwB 的价值网络只作为 baseline，不评价策略网络，用于降低随机梯度造成的方差；
  • A2C 的价值网络时critic，评价策略网络；

• RwB 是 A2C 的特殊形式。这一点下面 14.7 后会讲。

14.7 A2C with m-step

单步 A2C 就是上面所讲的内容，具体请见 14.5.b。

而多步A2C就是使用 m 个连续 transition：

• yt=∑m−1i=0γi⋅rt+1+γm⋅v(st+m;w)y_t=\sum_{i=0}^{m-1}\gammai\cdot r_{t+1}+\gamma^m\cdot v(s_{t+m};w)
• 具体参见m-step
• 剩下的步骤没有任何改变，只是 TD target 改变了。

下面解释 RwB 和 A2C with m-step 的关系：

• A2C with m-step 的TD target：yt=∑m−1i=0γi⋅rt+1+γm⋅v(st+m;w)y_t=\sum_{i=0}^{m-1}\gammai\cdot r_{t+1}+\gamma^m\cdot v(s_{t+m};w)
• 如果使用所有的奖励，上面两项中的第二项（估计）就不存在，而第一项变成了
  • yt=ut=∑ni=tγi−t⋅riy_t=u_t=\sum_{i=t}^n \gamma^{i-t}\cdot r_i
  • 这就是 Reinforce with baseline.

x. 参考教程

• 视频课程：深度强化学习（全）_哔哩哔哩_bilibili
• 视频原地址：https://www.youtube.com/user/wsszju
• 课件地址：https://github.com/wangshusen/DeepLearning