(python)常用算法-查找算法
前言
Python 中常用的算法有很多,分析一下实现的原理和demo.查找算法:线性查找, 二分查找,插值查找, 哈希查找,二叉查找树, 平衡二叉查找树, B树, 布隆过滤器等.
时间复杂度
| 算法 | 时间复杂度 |
| 顺序查找 | O(n) |
| 二分查找 | O(log n) |
| 插值查找 | O(log n) |
| 斐波那契查找 | O(log n) |
| 哈希查找 | O(1) |
| 二叉查找树 | O(log n) - O(n) |
| 平衡二叉树 | O(log n) |
| B树 | O(log n) |
| 布隆过滤器 | O(k) (k是位数组的长度) |
常用的算法类型和清单
Python常用的查找算法包括:
1. 线性查找(Linear Search):逐个遍历列表,直到找到目标元素或遍历完整个列表。
2. 二分查找(Binary Search):对于已排序的列表,将列表分成两半并比较中间元素与目标元素的大小,然后根据比较结果确定在哪一半继续查找,直到找到目标元素或确定不存在。
3. 插值查找(Interpolation Search):类似于二分查找,但是根据目标元素与列表中最大值和最小值的关系,通过插值计算出一个更接近目标元素的位置,从而加快搜索速度。
4. 哈希查找(Hash Search):将数据存储在哈希表中,通过计算目标元素的哈希值来确定其在哈希表中的位置,从而快速找到目标元素。
5. 二叉查找树(Binary Search Tree):将数据存储在一个二叉树中,根据节点值的大小关系来快速定位目标元素。
6. 平衡二叉查找树(Balanced Binary Search Tree):在二叉查找树的基础上,通过旋转操作保持树的平衡,提高查找效率,例如红黑树、AVL树等。
7. B树(B-Tree):一种自平衡的查找树,特别适合存储在磁盘等外部存储设备上的大规模数据。
8. 布隆过滤器(Bloom Filter):一种基于概率的查找数据结构,用于快速判断一个元素是否可能存在于集合中,但无法确定元素具体位置。
这些算法根据不同的场景和数据结构选择使用,每个算法都有其优缺点和适用范围。
线性查找
具体步骤
在一个无序列表中查找特定元素的位置,逐个对比,一旦找到元素就返回元素对应的索引.
代码示例
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i # 返回元素在列表中的索引
return -1 # 如果未找到目标元素,返回-1
# 示例使用
arr = [4, 2, 7, 1, 9, 5]
target = 7
result = linear_search(arr, target)
if result != -1:
print(f"目标元素 {target} 在列表中的索引为 {result}")
else:
print("未找到目标元素")
二分查找
一种在有序数组中查找目标值的算法。它的基本思想是将数组分为左右两部分,然后通过比较目标值与数组中间元素的大小关系,来确定目标值可能在哪一部分中,从而缩小查找范围。
具体步骤
arr 是有序数组,target 是待查找的目标值。算法首先初始化左右指针 left 和 right 分别指向数组的起始位置和结束位置。然后进入循环,每次取中间位置的元素 arr[mid] 进行比较,如果与目标值相等,则返回中间位置 mid。如果 arr[mid] 小于目标值,则说明目标值可能在右半部分,更新左指针 left 为 mid + 1。如果 arr[mid] 大于目标值,则说明目标值可能在左半部分,更新右指针 right 为 mid - 1。循环继续,直到左指针大于右指针,表示查找范围为空,返回 -1 表示未找到目标值。
代码示例
def binary_search(arr, target):
left = 0
right = len(arr) - 1
while left <= right:
mid = (left + right) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
插值查找
一种在有序数组中快速定位元素的算法,它利用元素在数组中的分布规律进行查找。
具体步骤
- 确定查找范围的上下界,通常是列表的首尾元素。
- 根据目标元素的估计位置,计算出一个插值索引。这个插值索引公式可以是
(目标元素 - 列表的首元素) / (列表的尾元素 - 列表的首元素)。 - 比较插值索引处的元素与目标元素的大小关系:
- 如果插值索引处的元素等于目标元素,则查找成功。
- 如果插值索引处的元素大于目标元素,则在插值索引的左侧继续查找。
- 如果插值索引处的元素小于目标元素,则在插值索引的右侧继续查找。
- 重复步骤 2 和步骤 3,直到找到目标元素或者查找范围为空。
代码示例
def interpolation_search(arr, target):
low = 0
high = len(arr) - 1
while low <= high and target >= arr[low] and target <= arr[high]:
if low == high:
if arr[low] == target:
return low
return -1
pos = low + int(((float(high - low) / (arr[high] - arr[low])) * (target - arr[low])))
if arr[pos] == target:
return pos
if arr[pos] < target:
low = pos + 1
else:
high = pos - 1
return -1
哈希查找
一种通过哈希函数将键映射到存储位置的查找技术。
具体步骤
在Python中,可以使用字典(dict)数据结构来实现哈希查找。字典是一种无序的键值对集合,其中每个键都是独一无二的。在哈希查找中,首先需要定义一个哈希函数,它将输入的键映射到一个固定大小的数组索引。常见的哈希函数有取余法、乘法哈希法等。然后,使用哈希函数计算键的哈希值,并将该值作为索引在数组中查找对应的值。
代码示例
# 创建一个包含学生信息的字典
students = {
1001: "Alice",
1002: "Bob",
1003: "Charlie",
1004: "David",
1005: "Eve"
}
# 定义哈希函数,这里简单地将键除以10取余
def hash_func(key):
return key % 10
# 哈希查找函数
def hash_search(key, hash_table):
index = hash_func(key)
if index in hash_table:
return hash_table[index]
else:
return None
# 使用哈希查找函数查找学生信息
student_id = 1003
result = hash_search(student_id, students)
if result:
print(f"Student with ID {student_id} is {result}")
else:
print(f"Student with ID {student_id} not found")
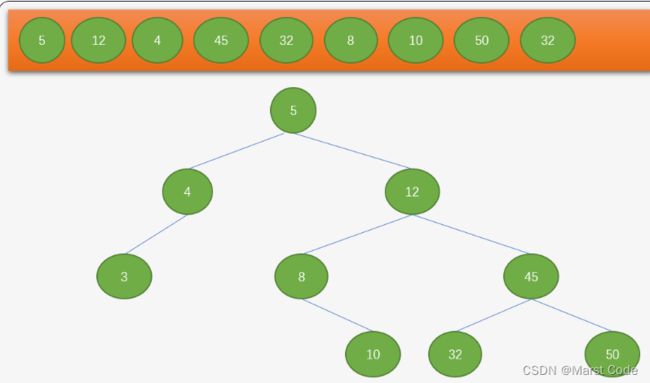
二叉查找树
特性:
- 每个节点最多有两个子节点,分别称为左子节点和右子节点。
- 左子节点的值小于父节点的值,右子节点的值大于父节点的值。
- 对于每个节点来说,其左子树和右子树也都是二叉查找树。
数据结构
具体步骤
定义一个Node类来表示二叉查找树的节点,然后再定义一个BinarySearchTree类来实现相关操作。实现了二叉查找树的插入操作和搜索操作。
代码示例
class Node:
def __init__(self, value):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
if self.root is None:
self.root = Node(value)
else:
self._insert_recursive(self.root, value)
def _insert_recursive(self, node, value):
if value < node.value:
if node.left is None:
node.left = Node(value)
else:
self._insert_recursive(node.left, value)
else:
if node.right is None:
node.right = Node(value)
else:
self._insert_recursive(node.right, value)
def search(self, value):
return self._search_recursive(self.root, value)
def _search_recursive(self, node, value):
if node is None or node.value == value:
return node
if value < node.value:
return self._search_recursive(node.left, value)
else:
return self._search_recursive(node.right, value)
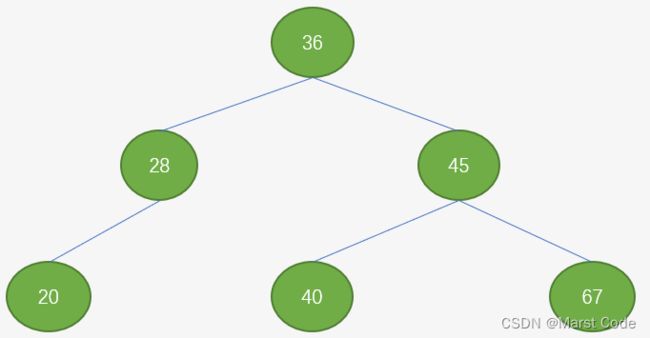
平衡二叉查找树
平衡二叉查找树(AVL树)是一种特殊的二叉查找树,它的每个节点的左子树和右子树的高度差不超过1。
数据结构
具体步骤
略...
代码示例
class TreeNode:
def __init__(self, key, left=None, right=None, height=1):
self.key = key
self.left = left
self.right = right
self.height = height
class AVLTree:
def __init__(self):
self.root = None
def insert(self, key):
self.root = self._insert(self.root, key)
def _insert(self, node, key):
if not node:
return TreeNode(key)
if key < node.key:
node.left = self._insert(node.left, key)
else:
node.right = self._insert(node.right, key)
node.height = 1 + max(self._get_height(node.left), self._get_height(node.right))
balance = self._get_balance(node)
if balance > 1:
if key < node.left.key:
return self._rotate_right(node)
else:
node.left = self._rotate_left(node.left)
return self._rotate_right(node)
if balance < -1:
if key > node.right.key:
return self._rotate_left(node)
else:
node.right = self._rotate_right(node.right)
return self._rotate_left(node)
return node
def _get_height(self, node):
if not node:
return 0
return node.height
def _get_balance(self, node):
if not node:
return 0
return self._get_height(node.left) - self._get_height(node.right)
def _rotate_left(self, z):
y = z.right
T2 = y.left
y.left = z
z.right = T2
z.height = 1 + max(self._get_height(z.left), self._get_height(z.right))
y.height = 1 + max(self._get_height(y.left), self._get_height(y.right))
return y
def _rotate_right(self, y):
x = y.left
T2 = x.right
x.right = y
y.left = T2
y.height = 1 + max(self._get_height(y.left), self._get_height(y.right))
x.height = 1 + max(self._get_height(x.left), self._get_height(x.right))
return x
B树(B-Tree)
B树是一种自平衡的搜索树数据结构,它可以高效地支持查找、插入和删除操作。
具体步骤
- 需要定义一个B树节点的类,节点包含关键字列表、子节点指针列表和一个布尔变量,用于表示该节点是否为叶子节点。
- 定义B树类,其中包含插入和查找操作。
- 在查找操作中,我们首先在当前节点中顺序查找关键字,如果找到则返回True。如果当前节点为叶子节点,则表示没有找到关键字,返回False。否则,我们根据关键字的大小选择递归地在相应的子节点中查找。
代码示例
# 定义一个B树节点的类,节点包含关键字列表、子节点指针列表和一个布尔变量,
# 用于表示该节点是否为叶子节点。
class BTreeNode:
def __init__(self, leaf=False):
self.leaf = leaf
self.keys = []
self.child = []
# 定义B树类,其中包含插入和查找操作
class BTree:
def __init__(self, t):
self.root = BTreeNode(True)
self.t = t
def search(self, k):
return self._search(self.root, k)
def _search(self, node, k):
# 在当前节点中查找关键字
i = 0
while i < len(node.keys) and k > node.keys[i]:
i += 1
# 如果找到关键字,则返回True
if i < len(node.keys) and k == node.keys[i]:
return True
# 如果当前节点为叶子节点,则说明没有找到关键字
if node.leaf:
return False
# 否则递归地在子节点中查找关键字
return self._search(node.child[i], k)
布隆过滤器(Bloom Filter)
布隆过滤器由一个位数组和多个哈希函数组成。
初始时,位数组的所有位都被置为0。当一个元素要被加入集合时,通过多个哈希函数将该元素映射到位数组的多个位置,并将这些位置的位都置为1。当判断一个元素是否在集合中时,同样通过多个哈希函数将该元素映射到位数组的对应位置,如果这些位置的位都为1,则认为该元素可能存在于集合中;如果其中任意一个位置的位为0,则可以确定该元素一定不存在于集合中。
具体步骤
-
初始化布隆过滤器:
- 创建一个位数组(bit array)或位向量(bit vector),用来表示集合。
- 初始化位数组的所有位为0。
- 设置哈希函数的数量和参数。
-
添加元素:
- 将要添加的元素输入到哈希函数中,并得到多个哈希值。
- 根据得到的哈希值,在位数组中将对应位置的位设置为1。
-
查询元素:
- 将要查询的元素输入到哈希函数中,并得到多个哈希值。
- 检查位数组中对应位置的位是否都为1,如果有任何一个位置的位为0,则说明元素不存在;如果所有位置的位都为1,则说明元素可能存在。
在这个实现中,我们使用了 mmh3 哈希算法来生成多个不同的哈希函数,以便在布隆过滤器中使用。我们还使用了 bitarray 库来创建位数组,用于表示布隆过滤器的位集合。
代码示例
import mmh3
from bitarray import bitarray
class BloomFilter:
def __init__(self, size, hash_count):
self.size = size
self.hash_count = hash_count
self.bit_array = bitarray(size)
self.bit_array.setall(0)
def add(self, item):
for seed in range(self.hash_count):
index = mmh3.hash(item, seed) % self.size
self.bit_array[index] = 1
def __contains__(self, item):
for seed in range(self.hash_count):
index = mmh3.hash(item, seed) % self.size
if self.bit_array[index] == 0:
return False
return True
# 示例用法
bf = BloomFilter(100000, 5)
bf.add("apple")
bf.add("banana")
print("apple" in bf) # 输出 True
print("orange" in bf) # 输出 False