2022蓝桥杯学习——6.双指针、BFS和图论

一、双指针

关于双指针

核心思想就是优化！！

双指针只用一层循环，虽然里面是while，但j只执行了n次，所以ij一共就是2n，时间复杂度就是O(n) , 这种题一般先写出暴力算法，然后看单调性，如果有单调性就可以用双指针来优化了（有的题目可能会说单调递增的数组之类的）

常见问题分类：
(1) 对于一个序列，用两个指针维护一段区间
(2) 对于两个序列，维护某种次序，比如归并排序中合并两个有序序列的操作

蓝桥杯真题

1.日志统计

题目描述
小明维护着一个程序员论坛。现在他收集了一份”点赞”日志，日志共有 N 行。

其中每一行的格式是：

ts id
表示在 ts 时刻编号 id 的帖子收到一个”赞”。

现在小明想统计有哪些帖子曾经是”热帖”。

如果一个帖子曾在任意一个长度为 D 的时间段内收到不少于 K 个赞，小明就认为这个帖子曾是”热帖”。

具体来说，如果存在某个时刻 T 满足该帖在 [T,T+D) 这段时间内(注意是左闭右开区间)收到不少于 K 个赞，该帖就曾是”热帖”。

给定日志，请你帮助小明统计出所有曾是”热帖”的帖子编号。

输入格式
第一行包含三个整数 N,D,K。

以下 N 行每行一条日志，包含两个整数 ts 和 id。

输出格式
按从小到大的顺序输出热帖 id。

每个 id 占一行。

数据范围
1≤K≤N≤10^5,
0≤ts,id≤10^5,
1≤D≤10000

输入样例：

7 10 2
0 1
0 10
10 10
10 1
9 1
100 3
100 3

输出样例：

1
3

解题思路

如果用暴力来写，每次统计一个时间段内出现的所有的id，用一个数组来存，每次统计完判断这个id出现的次数是否>=k，如果满足条件就将id标记为是热帖，最后遍历所有id输出，但是这样，一个for循环是时间段，还有一个for循环是所有id，根据D和id的范围可知一定超时了，所以将一层循环优化。每次循环下一个时间段，只是将时间往后偏移一个，下一次的循环统计的id跟上一次统计的id，只有前面的时间段和后面的时间段内的id不一样，中间都是重复统计的。
双指针优化：将所有的时间点排序，从前往后，指针 i 在前，j 指针在后，两个指针维护一个时间段，用 i 遍历所有时间点，每次将这个时间点被点赞的id 记录加一，并在每次判断点赞次数是否大于等于k 之前，判断当前点赞的时间点是否 还在时间段内，也就是 i 指向的时间点减去 j 指向的时间点是否大于等于d，如果是，将 j 往后移来缩小区间，并将不在时间段内的 id 点赞次数减一，其实 j 往后移之前指向的时间点的id 就是时间段之外的。

代码实现+详细注释C++

#include
#include
#include
#define x first
#define y second
using namespace std;
const int N=100010;
typedef pair<int,int> PII;
PII log[N];
bool st[N];
int cnt[N];
int n,d,k;

int main()
{
    cin>>n>>d>>k;
    for(int i=0;i<n;i++) cin>>log[i].x>>log[i].y;
    
    sort(log,log+n);
    
    for(int i=0,j=0;i<n;i++)
    {
        int id=log[i].y;
        cnt[id]++;//将时间段内的id记录加一
        while(log[i].x-log[j].x>=d)//如果不在这个时间段内了
        {
            cnt[log[j].y]--;//记录减一
            j++;//j 指针后移缩小时间段
        }
        if(cnt[id]>=k) st[id]=true;//如果这个id被点赞的次数大于等于 k 就将它标记为热帖
    }
    for(int i=0;i<=100000;i++)//输出所有为热帖的id，因为id的范围是0~1e5
        if(st[i]) cout<<i<<endl;
        
    return 0;
}

2.完全二叉的权值

题目描述
给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 A1,A2,⋅⋅⋅AN，如下图所示：

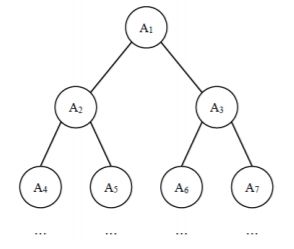
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？

如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 1。

输入格式
第一行包含一个整数 N。

第二行包含 N 个整数 A1,A2,⋅⋅⋅AN。

输出格式
输出一个整数代表答案。

数据范围
1≤N≤105,
−105≤Ai≤105
输入样例：

7
1 6 5 4 3 2 1

输出样例：

2

解题思路

计算权值最大的层数，我们可以计算出每一层的权值是多少，将所有权值作比较，得到权值最大的层数，观察可以得出，第i 层的第一个结点下标是2^(i-1)， 最后一个结点下标是2^i -1，所以用i 控制层数，用j 遍历每一层的结点，将权值累加，每一层算完比较权值，记录权值最大的，和权值最大的层数。

代码实现+详细注释C++

#include
#include
#include
#include
using namespace std;
const int N=100010;
int tr[N];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++) cin>>tr[i];
    long long maxw=-9223372036854775807,h=1;
    for(int i=1;;i++)//i是用来控制层数的
    {
        long long res=0;
        int m=pow(2,i-1);
        if(m>n){//当第i层第一个结点大于n，说明已经计算完所有层数了，输出结束
            cout<<h<<endl;
            return 0;
        }
        
        for(int j=m;j<=2*m-1&&j<=n;j++)//j 遍历每一层的结点 如果是满的，就是从m 到 2*m-1, 最后一层不一定是满的，所以要加一个判断j<=n，不然可能越界
        {
            res+=tr[j];
        }
        if(res>maxw)
        {
            maxw=res;
            h=i;
        }
    }
    return 0;
}

例题

二、BFS

关于BFS

大家可以参考这个博客里的图的遍历：图论

bfs–广度优先搜索

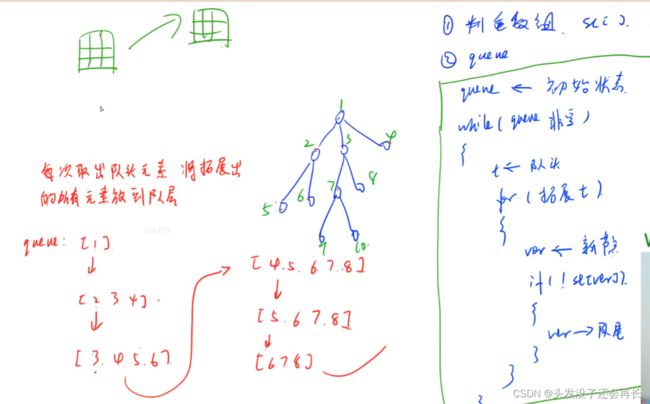
一层一层的访问，遍历所有结点，因此要有有个队列来存放每一个节点的所有相邻结点，直到队列为空，一般在求较短路的时候有bfs，例：

queue<int> q;
st[1] = true; // 表示1号点已经被遍历过
q.push(1);

while (q.size())
{
    int t = q.front();
    q.pop();

    for (int i = h[t]; i != -1; i = ne[i])
    {
        int j = e[i];
        if (!st[j])
        {
            st[j] = true; // 表示点j已经被遍历过
            q.push(j);
        }
    }
}

蓝桥杯真题

1.全球变暖

题目描述
你有一张某海域 N×N 像素的照片，”.”表示海洋、”#”表示陆地，如下所示：

…
.##…
.##…
…##.
…####.
…###.
…
其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿，例如上图就有 2 座岛屿。

由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。

具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。

例如上图中的海域未来会变成如下样子：

…
…
…
…
…#…
…
…
请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入格式
第一行包含一个整数N。

以下 N 行 N 列，包含一个由字符”#”和”.”构成的 N×N 字符矩阵，代表一张海域照片，”#”表示陆地，”.”表示海洋。

照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。

输出格式
一个整数表示答案。

数据范围
1≤N≤1000
输入样例1：

7
…
.##…
.##…
…##.
…####.
…###.
…

输出样例1：

1

输入样例2：

9
…
.##.##…
.#####…
.##.##…
…
.##.#…
.#.###…
.#…#…
…

输出样例2：

1

解题思路

由题意可知，所有的岛屿数量=连通块的数量，求联通块的小知识：对一个图用dfs或者bfs遍历，遍历的时候将走过的点都打上标记，每一次dfs或者bfs之后如果还有未遍历的点，继续dfs或者bfs，那么 有几次dfs或者bfs，就有几个连通块。此题要求不会消失的岛屿，其实就是看每个岛屿（连通块）中是否最少有一个陆地和海洋不相邻，如果有，这个岛屿就不会消失，最后用总共的岛屿数量减去不会消失的岛屿数量就是会消失的岛屿数量，所以在dfs求连通块的时候，可以对每一个连通块判断一下是不是存在这样的陆地不与海洋相邻即可，每次bfs结束，统计不会消失的岛屿。

代码实现+详细注释C++

#include
#include
#include
#include
#include
using namespace std;
const int N=1010;
#define x first
#define y second
typedef pair<int,int> PII;
char g[N][N];
int st[N][N];
int n;
bool flag;
int res,sum;
int dx[]={0,0,1,-1},dy[]={1,-1,0,0};
void bfs(int a,int b)
{
    
    queue<PII> q;
    q.push({a,b});
    st[a][b]=0;
    while(!q.empty())
    {
        auto t=q.front();
        q.pop();
        for(int i=0;i<4;i++)
        {
            int x=t.x+dx[i],y=t.y+dy[i];
            if(x<0||x>=n||y<0||y>=n) continue;
            if(st[x][y]!=-1) continue;
            if(g[x][y]!='#') continue;
            st[x][y]=st[t.x][t.y]+1;
            q.push({x,y});
            bool is;
            if(flag==false)//在每一个连通块找是否有一块陆地不与海洋相连，如果有，那么这个岛屿就不会消失
            {
                is=true;
                for(int j=0;j<4;j++)
                    if(g[x+dx[j]][y+dy[j]]=='.') is=false; 
            }
            flag=is;
        }
    }
}
int main()
{
    cin>>n;
    memset(st,-1,sizeof(st));
    for(int i=0;i<n;i++) cin>>g[i];
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
        {
            if(st[i][j]==-1&&g[i][j]=='#')
            {
                sum++;//统计多少个连通块，也就是多少个岛屿
                flag=false;//如果岛屿会消失，flag=false，反之，flag=true
                bfs(i,j);
                if(flag) res++;//统计不会消失的岛屿数量
            }
        }
    cout<<sum-res<<endl;
    return 0;
}

例题

1.献给阿尔吉侬的花束

题目描述
阿尔吉侬是一只聪明又慵懒的小白鼠，它最擅长的就是走各种各样的迷宫。

今天它要挑战一个非常大的迷宫，研究员们为了鼓励阿尔吉侬尽快到达终点，就在终点放了一块阿尔吉侬最喜欢的奶酪。

现在研究员们想知道，如果阿尔吉侬足够聪明，它最少需要多少时间就能吃到奶酪。

迷宫用一个 R×C 的字符矩阵来表示。

字符 S 表示阿尔吉侬所在的位置，字符 E 表示奶酪所在的位置，字符 # 表示墙壁，字符 . 表示可以通行。

阿尔吉侬在 1 个单位时间内可以从当前的位置走到它上下左右四个方向上的任意一个位置，但不能走出地图边界。

输入格式
第一行是一个正整数 T，表示一共有 T 组数据。

每一组数据的第一行包含了两个用空格分开的正整数 R 和 C，表示地图是一个 R×C 的矩阵。

接下来的 R 行描述了地图的具体内容，每一行包含了 C 个字符。字符含义如题目描述中所述。保证有且仅有一个 S 和 E。

输出格式
对于每一组数据，输出阿尔吉侬吃到奶酪的最少单位时间。

若阿尔吉侬无法吃到奶酪，则输出“oop!”（只输出引号里面的内容，不输出引号）。

每组数据的输出结果占一行。

数据范围
1 2≤R,C≤200
输入样例：

3
3 4
.S…
###.
…E.
3 4
.S…
.E…
…
3 4
.S…
####
…E.

输出样例：

5
1
oop!

解题思路

看到迷宫+最短路就可以考虑bfs来解题，为什么bfs可以求最短路，因为bfs每次遍历一层，从起点s开始，然后遍历s+1，s+2…，那么如果想找到某个点，最先找到的，一定是距离起点最近的。 bfs通常借助队列，将顶点入队，用一个while循环，当队不空的时候，将队首出队并将队首相邻的且为入队过的点入队，直到队空。

代码实现+详细注释C++

#include
#include
#include
#include
#include
using namespace std;

#define x first
#define y second
typedef pair<int,int> PII;
const int N=210;
char g[N][N];
int dist[N][N];
int n,r,c;
int dx[]={0,0,-1,1},dy[]={-1,1,0,0};//这两个数组对应四个方向 左、右、上、下

int bfs(PII start,PII end)
{
    queue<PII> q;
    dist[start.x][start.y]=0; //标记为已遍历
    q.push(start); //加入队尾
    while(!q.empty())
    {
        auto t=q.front();//取出队首
        q.pop();//出队
        for(int i=0;i<4;i++)//四个方向都判断
        {
            int x=t.x+dx[i],y=t.y+dy[i];
            if(x<0||x>=r||y<0||y>=c) continue;//越界
            if(g[x][y]=='#') continue;//障碍
            if(dist[x][y]!=-1) continue;//已遍历
            
            dist[x][y]=dist[t.x][t.y]+1;//可以走通，当前步数等于上一步加一
            
            if(end==make_pair(x,y)) return dist[x][y];//如果找到了奶酪，返回步数即可
            q.push({x,y});//没有找到，将当前点入队
        }
    }
    return -1;//不能找到奶酪，返回-1
}
int main()
{
    cin>>n;
    PII start,end;
    while(n--){
        cin>>r>>c;
        memset(dist,-1,sizeof(dist));
        for(int i=0;i<r;i++) scanf("%s",g[i]);
        for(int i=0;i<r;i++)
            for(int j=0;j<c;j++)
                if(g[i][j]=='S') start={i,j};
                else if(g[i][j]=='E') end={i,j};
       
        int dis=bfs(start,end);
        if(dis==-1) cout<<"oop!"<<endl;
        else cout<<dis<<endl;
    
    }
    return 0;
}

2.红与黑

题目描述
有一间长方形的房子，地上铺了红色、黑色两种颜色的正方形瓷砖。

你站在其中一块黑色的瓷砖上，只能向相邻（上下左右四个方向）的黑色瓷砖移动。

请写一个程序，计算你总共能够到达多少块黑色的瓷砖。

输入格式
输入包括多个数据集合。

每个数据集合的第一行是两个整数 W 和 H，分别表示 x 方向和 y 方向瓷砖的数量。

在接下来的 H 行中，每行包括 W 个字符。每个字符表示一块瓷砖的颜色，规则如下

1）‘.’：黑色的瓷砖；
2）‘#’：红色的瓷砖；
3）‘@’：黑色的瓷砖，并且你站在这块瓷砖上。该字符在每个数据集合中唯一出现一次。

当在一行中读入的是两个零时，表示输入结束。

输出格式
对每个数据集合，分别输出一行，显示你从初始位置出发能到达的瓷砖数(记数时包括初始位置的瓷砖)。

数据范围
1≤W,H≤20
输入样例：

6 9
…#.
…#
…
…
…
…
…
#@…#
.#…#.
0 0

输出样例：

45

解题思路

代码与上一题基本雷同，但是，不同的是，上一道题求最短路，这道题是求最多能走多少格，所以上一题只要求走到终点的dist，但是这道题要在每一个可以走的位置将总步数加一，直到队空，不能继续走
bfs和dfs都可以解题

代码实现+详细注释C++
bfs

#include
#include
#include
#include
#include
using namespace std;

#define x first
#define y second
const int N=25;
int dx[]={0,0,1,-1},dy[]={-1,1,0,0};
typedef pair<int,int> PII;
int dist[N][N];
char g[N][N];
int n,m;
int bfs(PII start)
{
    int res=1;
    queue<PII> q;
    dist[start.x][start.y]=0;
    q.push({start.x,start.y});
    while(!q.empty())
    {
        auto t=q.front();
        q.pop();
        for(int i=0;i<4;i++)
        {
            int x=t.x+dx[i],y=t.y+dy[i];
            if(x<0||x>=n||y<0||y>=m) continue;
            if(g[x][y]!='.') continue;
            if(dist[x][y]!=-1) continue;
            
            dist[x][y]=dist[t.x][t.y]+1;
            res++;//只要能遍历到，就将结果加一
            q.push({x,y});
        }
    }
    return res;
}
int main()
{
    
    PII start;
    while(1)
    {
        memset(dist,-1,sizeof(dist));
        cin>>m>>n;
        if(n==0&&m==0) return 0;
        for(int i=0;i<n;i++) cin>>g[i];
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                if(g[i][j]=='@') start={i,j};
        cout<<bfs(start)<<endl;
    }
    return 0;
}

dfs

#include
#include
#include
using namespace std;
const int N=25;
char g[N][N];
int st[N][N];
int n,m;
int dx[]={0,0,-1,1},dy[]={-1,1,0,0};
int dfs(int x,int y)
{
    st[x][y]=true;
    int res=1;
    for(int i=0;i<4;i++)
    {
        int x1=dx[i]+x,y1=dy[i]+y;
        if(x1<0||x1>=n||y1<0||y1>=m) continue;
        if(g[x1][y1]!='.') continue;
        if(st[x1][y1]) continue;
        res+=dfs(x1,y1);
    }
    return res;
}
int main()
{
    
    while(1)
    {
        cin>>m>>n;
        memset(st,0,sizeof(st));
        int x,y;
        if(n==0&&m==0) return 0;
        for(int i=0;i<n;i++) cin>>g[i];
        for(int i=0;i<n;i++)
            for(int j=0;j<m;j++)
                if(g[i][j]=='@'){
                    x=i,y=j;
                }
        cout<<dfs(x,y)<<endl;            
    }
    return 0;
}

3.地牢大师

题目描述
你现在被困在一个三维地牢中，需要找到最快脱离的出路！

地牢由若干个单位立方体组成，其中部分不含岩石障碍可以直接通过，部分包含岩石障碍无法通过。

向北，向南，向东，向西，向上或向下移动一个单元距离均需要一分钟。

你不能沿对角线移动，迷宫边界都是坚硬的岩石，你不能走出边界范围。

请问，你有可能逃脱吗？

如果可以，需要多长时间？

输入格式
输入包含多组测试数据。

每组数据第一行包含三个整数 L,R,C 分别表示地牢层数，以及每一层地牢的行数和列数。

接下来是 L 个 R 行 C 列的字符矩阵，用来表示每一层地牢的具体状况。

每个字符用来描述一个地牢单元的具体状况。

其中, 充满岩石障碍的单元格用”#”表示，不含障碍的空单元格用”.”表示，你的起始位置用”S”表示，终点用”E”表示。

每一个字符矩阵后面都会包含一个空行。

当输入一行为”0 0 0”时，表示输入终止。

输出格式
每组数据输出一个结果，每个结果占一行。

如果能够逃脱地牢，则输出”Escaped in x minute(s).”，其中X为逃脱所需最短时间。

如果不能逃脱地牢，则输出”Trapped!”。

数据范围
1≤L,R,C≤100
输入样例：

3 4 5
S…
.###.
.##…
###.#

#####
#####
##.##
##…

#####
#####
#.###
####E

1 3 3
S##
#E#
###

0 0 0

输出样例：

Escaped in 11 minute(s).
Trapped!

解题思路

这一题一样用bfs搜最短路，与之前不同的是，这道题有六个方向，其它的几乎没有变化，所以记住bfs模板很重要哦

代码实现+详细注释C++

#include
#include
#include
#include
#include
#include
using namespace std;
const int N=110;
char g[N][N][N];
int cnt[N][N][N];
int dx[]={0,0,-1,1,0,0},dy[]={-1,1,0,0,0,0},dz[]={0,0,0,0,1,-1};//六个方向 最后两个是上下
int l,r,c;
struct Node{
    int z,x,y;
}st,en;
int bfs()
{
    queue<struct Node> q;
    q.push({st.z,st.x,st.y});
    cnt[st.z][st.x][st.y]=0;//标记为已访问
    while(!q.empty())
    {
        auto t=q.front();
        q.pop();
        for(int i=0;i<6;i++)//遍历六个方向
        {
            int xx=t.x+dx[i],yy=t.y+dy[i],zz=t.z+dz[i];
            if(xx<0||xx>=r||yy<0||yy>=c||zz<0||zz>=l) continue;//越界
            if(g[zz][xx][yy]=='#') continue;//障碍物
            if(cnt[zz][xx][yy]!=-1) continue;//已遍历
            cnt[zz][xx][yy]=cnt[t.z][t.x][t.y]+1;//计算步数，也是标记已访问
            if(en.x==xx&&en.y==yy&&en.z==zz) return cnt[zz][xx][yy];//已到达终点
            q.push({zz,xx,yy});
            
        }
    }
    return -1;//无法到达返回-1
}
int main()
{
    while(scanf("%d%d%d",&l,&r,&c)&&l)
    {
        memset(cnt,-1,sizeof(cnt));
        for(int i=0;i<l;i++)//控制层数
        {
            for(int j=0;j<r;j++)//每一层的行数
            {
                string str;
                cin>>str;//每一行读入一个字符串
                for(int k=0;k<c;k++)//每一层的列数
                {
                    g[i][j][k]=str[k];//用字符给图赋值
                    if(str[k]=='S') st={i,j,k};
                    if(str[k]=='E') en={i,j,k};
                }
            }
        }
        int dist=bfs();
        if(dist==-1) cout<<"Trapped!"<<endl;
        else printf("Escaped in %d minute(s).\n",cnt[en.z][en.x][en.y]);
    }
    return 0;
}

三、图论

关于图论

推荐大家看这篇博客了解图论里的基础算法：图论

蓝桥杯真题

1.交换瓶子（图论，环，置换群，贪心）

题目描述
有 N 个瓶子，编号 1∼N，放在架子上。

比如有 5 个瓶子：

2 1 3 5 4

要求每次拿起 2 个瓶子，交换它们的位置。

经过若干次后，使得瓶子的序号为：

1 2 3 4 5

对于这么简单的情况，显然，至少需要交换 2 次就可以复位。

如果瓶子更多呢？你可以通过编程来解决。

输入格式
第一行包含一个整数 N，表示瓶子数量。

第二行包含 N 个整数，表示瓶子目前的排列状况。

输出格式
输出一个正整数，表示至少交换多少次，才能完成排序。

数据范围
1≤N≤10000,

输入样例1：

5
3 1 2 5 4

输出样例1：

3

输入样例2：

5
5 4 3 2 1

输出样例2：

2

解题思路

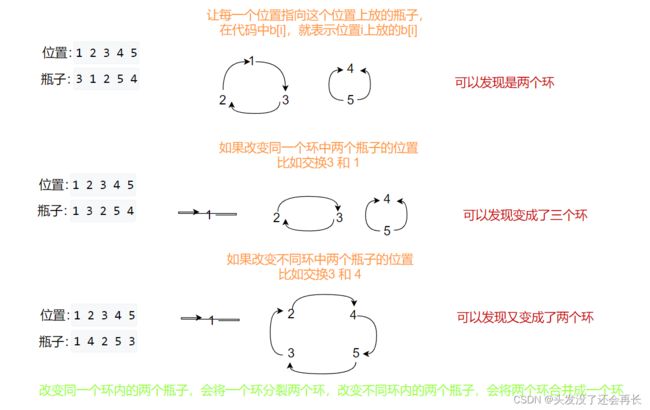
如果让每个位置都指向应该放的瓶子，那么
就会有n个自环，因为每个数都指向自己
如果操作同一个环内的连个瓶子，
就会将环 数量增加1，假设原本有k个环
我们的目的是使图中存在n个环，
所以至少需要n-k次操作
所以只需要求出图中存在多少个环即可

代码实现+详细注释C++

#include
#include
#include
using namespace std;
const int N=10010;
int b[N];
bool st[N];
int n,cnt;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++) cin>>b[i];
    
    for(int i=1;i<=n;i++)
    {
        if(!st[i])//如果未标记，说明在新的环里
        {
            cnt++;//将环的数量+1
            for(int j=i;!st[j];j=b[j])//将同一个环内的瓶子全部打上标记
                st[j]=true;
        }
    }
    cout<<n-cnt<<endl;
    return 0;
}

4.大臣的旅费

题目描述
很久以前，T王国空前繁荣。

为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。

为节省经费，T国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。

同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。

J是T国重要大臣，他巡查于各大城市之间，体察民情。

所以，从一个城市马不停蹄地到另一个城市成了J最常做的事情。

他有一个钱袋，用于存放往来城市间的路费。

聪明的J发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第x千米到第x+1千米这一千米中（x是整数），他花费的路费是x+10这么多。也就是说走1千米花费11，走2千米要花费23。

J大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入格式
输入的第一行包含一个整数 n，表示包括首都在内的T王国的城市数。

城市从 1 开始依次编号，1 号城市为首都。

接下来 n−1 行，描述T国的高速路（T国的高速路一定是 n−1 条）。

每行三个整数 Pi,Qi,Di，表示城市 Pi 和城市 Qi 之间有一条双向高速路，长度为 Di 千米。

输出格式
输出一个整数，表示大臣J最多花费的路费是多少。

数据范围
1≤n≤105,
1≤Pi,Qi≤n,
1≤Di≤1000
输入样例：

5
1 2 2
1 3 1
2 4 5
2 5 4

输出样例：

135

解题思路

因为从一个城市到另一个城市的路径是唯一的，所以图中没有环，且任意两个城市之间可达，所以是一个无环连通图也就是树。路费：走第一个千米，路费是10+1，走第二个千米，路费是10+2，走第s个千米，路费是10+s，走了s千米一共的路费就是10+1+10+2+…+10+s=10*s+（s+1）*s/2，求路费是一个单调递增的函数，所以求最大路费就是求s最大，就转化成了 求树中的一条最长路径，也被成为树的直径 。
1、任取一点x
2、找到距离x最远的点y（dfs）
3、从y开始遍历，找到离y最远的点，与y最远的点的距离是树的直径（dfs）

代码实现+详细注释C++

#include
#include
#include
#include
#include
#include
using namespace std;
const int N=100010;
struct Node
{
    int id,w;
};//用结构体存每个点相邻的顶点以及这条边的权值
vector<Node> h[N];
int dist[N];
void dfs(int u,int father,int distance)//因为是无向图，为了防止dfs的时候递归回去，要在dfs时保留根结点
{
    dist[u]=distance;
    for(auto node:h[u])
    {
        if(node.id!=father)
        {
            dfs(node.id,u,distance+node.w);
        }
    }
}
int main()
{
    int n;
    cin>>n;
    for(int i=0;i<n-1;i++)
    {
        int a,b,c;
        cin>>a>>b>>c;
        h[a].push_back({b,c});
        h[b].push_back({a,c});
    }
    
    //从首都开始，找到距离首都最远的点u
    dfs(1,-1,0);
    
    int u=1;
    for(int i=1;i<=n;i++)
    {
        if(dist[i]>dist[u]) u=i;
    }
    
    //从u开始找到距离u最远的距离就是直径
    dfs(u,-1,0);
    for(int i=1;i<=n;i++)
    {
        if(dist[i]>dist[u]) u=i;
    }
    int s=dist[u];//直径
    cout<<10*s+(s+1ll)*s/2<<endl;
    return 0;
}

总结:

双指针是一种思想，一种优化思想，虽然每次看起来像是两层循环，但其实大多数情况下每个元素只遍历一次
BFS和DFS一般是通用的，但是BFS可以求无权图或者每条边的权值是1的图的最短路径，而DFS不能，但如果只是遍历图，DFS和BFS都可以
图论大家可以参考这个博客：我学数据结构的时候总结的图，有图文详解，在蓝桥杯里图论考的不多，但是基本的一些了解还是好的，多掌握没有坏处

学习网站：AcWing