对背包问题(Knapsack Problem)的算法探究
对背包问题(Knapsack Problem)的算法探究
至繁归于至简,这次自己仍然用尽可能易理解和阅读的解决方式。


1、问题说明:
假设有一个背包的负重最多可达8公斤,而希望在背包中装入负重范围内可得之总价物品,假设是水果好了,水果的编号、单价与重量如下所示:
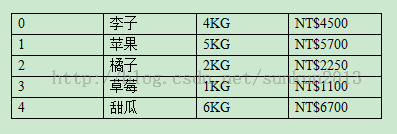
2、解法:
背包问题是关于最佳化的问题,要解最佳化问题可以使用「动态规划」(Dynamic programming),从空集合开始,每增加一个元素就先求出该阶段的最佳解,直到所有的元素加入至集合中,最后得到的就是最佳解。
以背包问题为例,我们使用两个阵列value与item,value表示目前的最佳解所得之总价,item表示最后一个放至背包的水果,假设有负重量 1~8的背包8个,并对每个背包求其最佳解。
逐步将水果放入背包中,并求该阶段的最佳解:
放入李子

放入苹果

放入橘子

放入草莓

放入甜瓜

由最后一个表格,可以得知在背包负重8公斤时,最多可以装入9050元的水果,而最后一个装入的 水果是3号,也就是草莓,装入了草莓,背包只能再放入7公斤(8-1)的水果,所以必须看背包负重7公斤时的最佳解,最后一个放入的是2号,也就 是橘子,现在背包剩下负重量5公斤(7-2),所以看负重5公斤的最佳解,最后放入的是1号,也就是苹果,此时背包负重量剩下0公斤(5-5),无法 再放入水果,所以求出最佳解为放入草莓、橘子与苹果,而总价为9050元。
3、具体代码:
/**
* @Title 对背包问题(Knapsack Problem)的算法探究
* @Author 孙琨
* @Date 2013-11-19
* @At XUST
* @All Copyright by 孙琨
*
*/
#include <stdio.h>
#define LIMIT 8
#define N 5
#define MIN 1
struct body
{
char name[20];
int size;
int price;
};
typedef struct body object;
int main(void)
{
int item[LIMIT + 1] = {0};
int value[LIMIT + 1] = {0};
int newvalue,i,s,p;
object a[] = {
{"李子",4,4500},
{"苹果",5,5700},
{"橘子",2,2250},
{"草莓",1,1100},
{"甜瓜",6,6700}
};
for(i=0; i<N; i++)
{
for(s=a[i].size; s<=LIMIT; s++)
{
p = s - a[i].size;
newvalue = value[p] + a[i].price;
if(newvalue > value[s]) // 找到阶段最佳解
{
value[s] = newvalue;
item[s] = i;
}
}
}
printf("物品\t价格\n");
for(i=LIMIT; i>=MIN; i=i-a[item[i]].size)
{
printf("%s\t%d\n",a[item[i]].name,a[item[i]].price);
}
printf("合计\t%d\n",value[LIMIT]);
return 0;
}
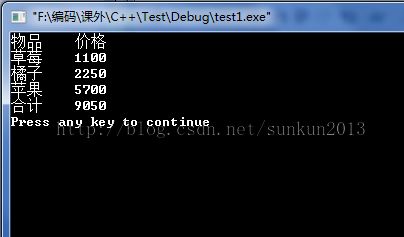
4、运行结果截图: