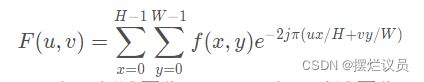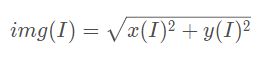OpenCV学习记录 三 （傅里叶逆变换原理及实现）

为什么要在频率域研究图像增强？

利用频率成分和图像外表之间的对应关系。滤波在频率域更为直观，它可以解释空间域滤波的某些性质。可以在频率域指定滤波器，做反变换，然后在空间域使用结果滤波器作为空间域滤波器的指导。一旦通过频率域试验选择了空间滤波，通常实施都在空间域进行。

傅里叶变换是为后面低通滤波或者说是高通滤波做准备，处理的是灰度图像。

一、傅里叶变换

傅里叶变换（Fourier Transform，FT）后，对同一事物的观看角度随之改变，可以从频域里发现一些从时域里不易察觉的特征。

原理：将满足一定条件的某个函数表示成三角函数(正弦/余弦函数)或者是二者的积分的线性组合，在不同的研究领域，傅里叶变换有不同的变体形式，连续傅里叶变换或者离散傅里叶变换。傅里叶变换是一种分析信号的方法，傅里叶变换用正弦波作为信号的成分。

傅里叶变换的实质是将一个信号分离为无穷多多正弦/复指数信号的加成，也就是说，把信号变成正弦信号相加的形式——既然是无穷多个信号相加，那对于非周期信号来说，每个信号的加权应该都是零——但有密度上的差别，你可以对比概率论中的概率密度来思考一下——落到每一个点的概率都是无限小，但这些无限小是有差别的所以，傅里叶变换之后，横坐标即为分离出的正弦信号的频率，纵坐标对应的是加权密度。

傅里叶变换的作用：

傅里叶变换可以将一个时域信号转换成在不同频率下对应的振幅及相位，其频谱就是时域信号在频域下的表现，而反傅里叶变换可以将频谱再转换回时域的信号。

图像进行傅里叶变换原理：

灰度图像是由二维的离散的点构成的。二维离散傅里叶变换常用于图像处理中，对图像进行傅里叶变换后得到其频谱图。频谱图中频率高低表征图像中灰度变化的剧烈程度。图像中边缘和噪声往往是高频信号，而图像背景往往是低频信号。我们在频率域内可以很方便地对图像的高频或低频信息进行操作，完成图像去噪，图像增强，图像边缘提取等操作。

 图像高H，宽W。F(u,v)表示频域图像，f(x,y)表示时域图像。u的范围为[0,H−1]，v的范围为[0,W−1]

使用OpenCV库函数实现傅里叶变换：

cv2.dft()是实数部分，cv2.magnitude()是虚数部分。

函数原型：img=cv2.dft(src, flags=None, nonzeroRows=None)

        #src：输入图像，需要通过np.float32转换格式
        #flags：转换标记，其中DFT _INVERSE执行反向一维或二维转换，而不是默认的正向转换 .          #DFT _SCALE表示缩放结果，由阵列元素的数量除以它；DFT _ROWS执行正向或反向变换输入矩阵的每个单独的行，该标志可以同时转换多个矢量，并可用于减少开销以执行3D和更高维度的转换等；DFT _COMPLEX_OUTPUT执行1D或2D实数组的正向转换，这是最快的选择，默认功能；DFT _REAL_OUTPUT执行一维或二维复数阵列的逆变换，结果通常是相同大小的复数数组，但如果输入数组具有共轭复数对称性，则输出为真实数组
        #nonzeroRows：当参数不为零时，函数假定只有nonzeroRows输入数组的第一行（未设置）或者只有输出数组的第一个（设置）包含非零，因此函数可以处理其余的行更有效率，并节省一些时间；这种技术对计算阵列互相关或使用DFT卷积非常有用。

由于输出的频谱结果是一个复数，需要调用cv2.magnitude()函数将傅里叶变换的双通道结果转换为0到255的范围

cv2.magnitude()函数原型：cv2.magnitude(x, y)

        #x表示浮点型X坐标值，即实部

        #y表示浮点型Y坐标值，即虚部

结果的值为： 

 代码如下：

import cv2
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] #显示中文
img=cv2.imread("jiesi.jpg",0)
#OpneCV傅里叶变换函数
result =cv2.dft(np.float32(img),flags = cv2.DFT_COMPLEX_OUTPUT)#需要将图像进行一次float转换
#将频谱低频从左上角移动至中心位置
dft_shift = np.fft.fftshift(result)
#频谱图像双通道复数转换为0-255区间
result1 = 20*np.log(cv2.magnitude(dft_shift[:,:,0], dft_shift[:,:,1]))
#图像显示
plt.subplot(121), plt.imshow(img,'gray'), plt.title('原图像')
plt.axis('off')
plt.subplot(122), plt.imshow(result1,'gray'), plt.title('傅里叶变换')
plt.axis('off')
plt.show()

效果图如下：

 使用Numpy库的图像傅里叶变换

import cv2 as cv
import numpy as np
from matplotlib import pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
img = cv.imread('jiesi.jpg',0)
#快速傅里叶变换算法得到频率分布
f = np.fft.fft2(img)
#默认结果中心点位置是在左上角,
#调用fftshift()函数转移到中间位置
fshift = np.fft.fftshift(f)
#fft结果是复数, 其绝对值结果是振幅
fimg = np.log(np.abs(fshift))
plt.subplot(121), plt.imshow(img,'gray'), plt.title('原图像')
plt.axis('off')
plt.subplot(122), plt.imshow(fimg,'gray'), plt.title('傅里叶变换')
plt.axis('off')
plt.show()

效果图如下：

傅里叶逆变换