【Python排序搜索基本算法】之Prim算法

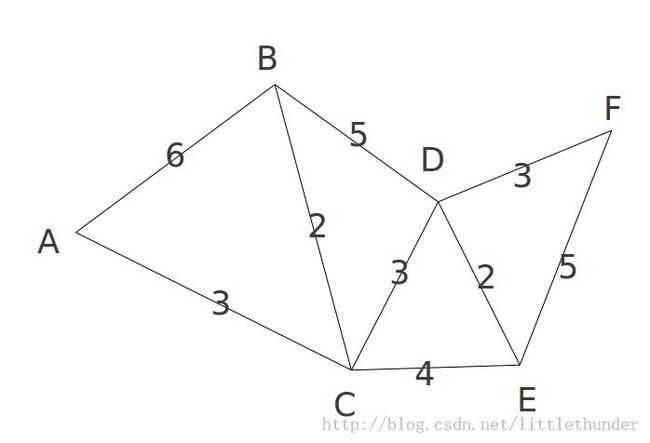
    Prim算法是实现最简单的最小生成树（MST）算法，适合于稠密图。要实现Prim算法，我们主要关注的是增量的变化，也就是从每个非树顶点到树顶点的最短距离，使得最后生成一棵包括所有顶点的树，并且这棵树的边权值之和最小。下面用一个例子说明：

代码如下：

 

_=float('inf')

def prim(graph,n):
	dis=[0]*n
	pre=[0]*n
	flag=[False]*n
	flag[0]=True
	k=0
	for i in range(n):
		dis[i]=graph[k][i]
	for j in range(n-1):
		mini=_
		for i in range(n):
			if mini>dis[i] and not flag[i]:
				mini=dis[i]
				k=i
		if k==0:#不连通
			return
		flag[k]=True
		for i in range(n):
			if dis[i]>graph[k][i] and not flag[i]:
				dis[i]=graph[k][i]
				pre[i]=k
	return dis,pre


if __name__=='__main__':
	n=6
	graph=[
			[0,6,3,_,_,_],
			[6,0,2,5,_,_],
			[3,2,0,3,4,_],
			[_,5,3,0,2,3],
			[_,_,4,2,0,5],
			[_,_,_,3,5,0],
			]
	dis,pre=prim(graph,n)
	print(dis)
	print(pre)

输出结果如下：

 

 

[0, 2, 3, 3, 2, 3]
[0, 2, 0, 2, 3, 3]

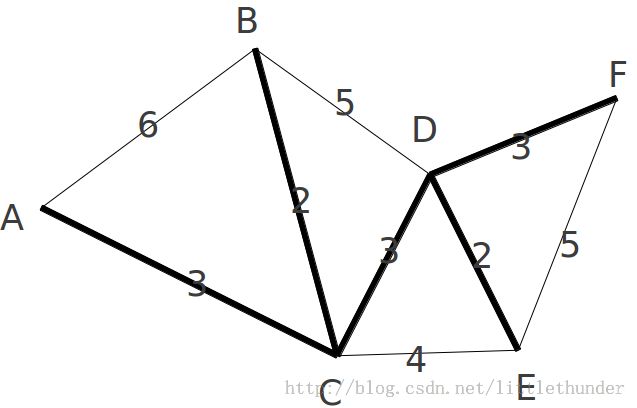
用粗边表示计算出的最小生成树如下：

 

转载请注明：转自 http://blog.csdn.net/littlethunder/article/details/9748361