Leetcode 01-算法入门与数组-②数组基础
LeetCode 01-算法入门与数组-②数组基础
一. 数组基础知识
1. 数组简介
1.1 数组定义
数组(Array):一种线性表数据结构。它使用一组连续的内存空间,来存储一组具有相同类型的数据。
简单来说,「数组」 是实现线性表的顺序结构存储的基础。
以整数数组为例,数组的存储方式如下图所示。
如上图所示,假设数据元素的个数为 n n n,则数组中的每一个数据元素都有自己的下标索引,下标索引从 0 0 0 开始,到 n − 1 n - 1 n−1 结束。数组中的每一个「下标索引」,都有一个与之相对应的「数据元素」。
从上图还可以看出,数组在计算机中的表示,就是一片连续的存储单元。数组中的每一个数据元素都占有一定的存储单元,每个存储单元都有自己的内存地址,并且元素之间是紧密排列的。
我们还可以从两个方面来解释一下数组的定义。
- 线性表:线性表就是所有数据元素排成像一条线一样的结构,线性表上的数据元素都是相同类型,且每个数据元素最多只有前、后两个方向。数组就是一种线性表结构,此外,栈、队列、链表都是线性表结构。
- 连续的内存空间:线性表有两种存储结构:「顺序存储结构」和「链式存储结构」。其中,「顺序存储结构」是指占用的内存空间是连续的,相邻数据元素之间,物理内存上的存储位置也相邻。数组也是采用了顺序存储结构,并且存储的数据都是相同类型的。
综合这两个角度,数组就可以看做是:使用了「顺序存储结构」的「线性表」的一种实现方式。
1.2 如何随机访问数据元素
数组的一个最大特点是:可以进行随机访问。即数组可以根据下标,直接定位到某一个元素存放的位置。
那么,计算机是如何实现根据下标随机访问数组元素的?
计算机给一个数组分配了一组连续的存储空间,其中第一个元素开始的地址被称为 「首地址」。每个数据元素都有对应的下标索引和内存地址,计算机通过地址来访问数据元素。当计算机需要访问数组的某个元素时,会通过 「寻址公式」 计算出对应元素的内存地址,然后访问地址对应的数据元素。
寻址公式如下:下标 i i i 对应的数据元素地址 = 数据首地址 + i i i × 单个数据元素所占内存大小。
1.3 多维数组
上面介绍的数组只有一个维度,称为一维数组,其数据元素也是单下标变量。但是在实际问题中,很多信息是二维或者是多维的,一维数组已经满足不了我们的需求,所以就有了多维数组。
以二维数组为例,数组的形式如下图所示。
二维数组是一个由 m m m 行 n n n 列数据元素构成的特殊结构,其本质上是以数组作为数据元素的数组,即 「数组的数组」。二维数组的第一维度表示行,第二维度表示列。
我们可以将二维数组看做是一个矩阵,并处理矩阵的相关问题,比如转置矩阵、矩阵相加、矩阵相乘等等。
1.4 不同编程语言中数组的实现
在具体的编程语言中,数组这个数据结构的实现方式具有一定差别。
C / C++ 语言中的数组最接近数组结构定义中的数组,使用的是一块存储相同类型数据的、连续的内存空间。不管是基本类型数据,还是结构体、对象,在数组中都是连续存储的。例如:
int arr[3][4] = {{0, 1, 2, 3}, {4, 5, 6, 7}, {8, 9, 10, 11}};
Java 中的数组跟数据结构定义中的数组不太一样。Java 中的数组也是存储相同类型数据的,但所使用的内存空间却不一定是连续(多维数组中)。且如果是多维数组,其嵌套数组的长度也可以不同。例如:
int[][] arr = new int[3][]{ {1,2,3}, {4,5}, {6,7,8,9}};
原生 Python 中其实没有数组的概念,而是使用了类似 Java 中的 ArrayList 容器类数据结构,叫做列表。通常我们把列表来作为 Python 中的数组使用。Python 中列表存储的数据类型可以不一致,数组长度也可以不一致。例如:
arr = ['python', 'java', ['asp', 'php'], 'c']
2. 数组的基本操作
数据结构的操作一般涉及到增、删、改、查共 4 4 4 种情况,下面我们一起来看一下数组的这 4 4 4 种基本操作。
2.1 访问元素
访问数组中第 i i i 个元素:
- 只需要检查 i i i 的范围是否在合法的范围区间,即 0 ≤ i ≤ l e n ( n u m s ) − 1 0 \le i \le len(nums) - 1 0≤i≤len(nums)−1。超出范围的访问为非法访问。
- 当位置合法时,由给定下标得到元素的值。
# 从数组 nums 中读取下标为 i 的数据元素值
def value(nums, i):
if 0 <= i <= len(nums) - 1:
print(nums[i])
arr = [0, 5, 2, 3, 7, 1, 6]
value(arr, 3)
「访问数组元素」的操作不依赖于数组中元素个数,因此,「访问数组元素」的时间复杂度为 O ( 1 ) O(1) O(1)。
2.2 查找元素
查找数组中元素值为 v a l val val 的位置:
- 建立一个基于下标的循环,每次将 v a l val val 与当前数据元素 n u m s [ i ] nums[i] nums[i] 进行比较。
- 在找到元素的时候返回元素下标。
- 遍历完找不到时可以返回一个特殊值(例如 − 1 -1 −1)。
# 从数组 nums 中查找元素值为 val 的数据元素第一次出现的位置
def find(nums, val):
for i in range(len(nums)):
if nums[i] == val:
return i
return -1
arr = [0, 5, 2, 3, 7, 1, 6]
print(find(arr, 5))
在「查找元素」的操作中,如果数组无序,那么我们只能通过将 v a l val val 与数组中的数据元素逐一对比的方式进行查找,也称为线性查找。而线性查找操作依赖于数组中元素个数,因此,「查找元素」的时间复杂度为 O ( n ) O(n) O(n)。
2.3 插入元素
插入元素操作分为两种:「在数组尾部插入值为 v a l val val 的元素」和「在数组第 i i i 个位置上插入值为 v a l val val 的元素」。
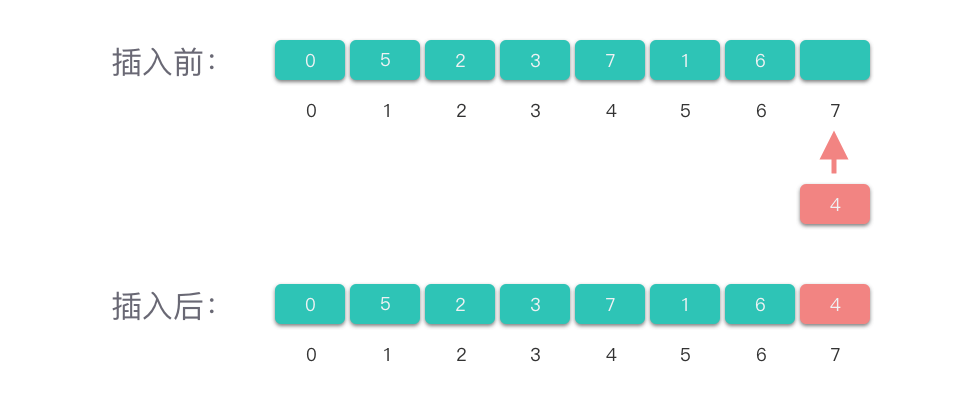
在数组尾部插入值为 v a l val val 的元素:
- 如果数组尾部容量不满,则直接把 v a l val val 放在数组尾部的空闲位置,并更新数组的元素计数值。
- 如果数组容量满了,则插入失败。不过,Python 中的 list 列表做了其他处理,当数组容量满了,则会开辟新的空间进行插入。
Python 中的 list 列表直接封装了尾部插入操作,直接调用 append 方法即可。
arr = [0, 5, 2, 3, 7, 1, 6]
val = 4
arr.append(val)
print(arr)
「在数组尾部插入元素」的操作不依赖数组个数,因此,「在数组尾部插入元素」的时间复杂度为 O ( 1 ) O(1) O(1)。
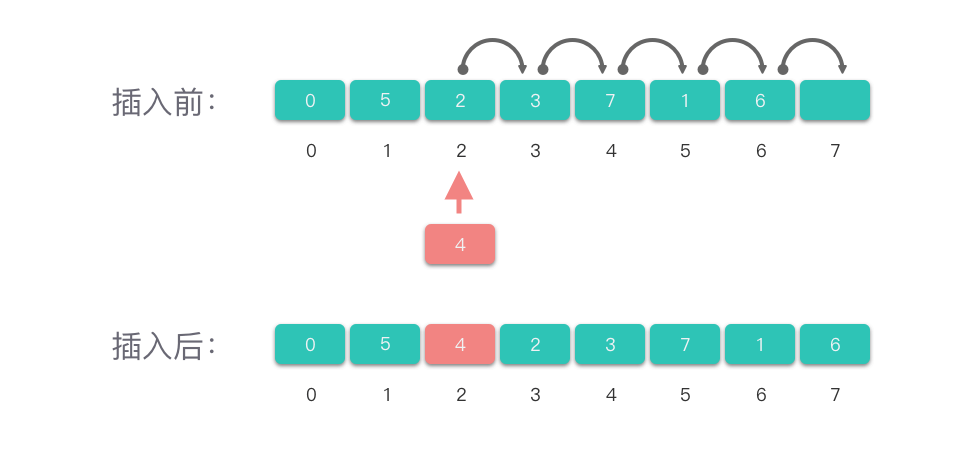
在数组第 i i i 个位置上插入值为 v a l val val 的元素:
- 先检查插入下标 i i i 是否合法,即 0 ≤ i ≤ l e n ( n u m s ) 0 \le i \le len(nums) 0≤i≤len(nums)。
- 确定合法位置后,通常情况下第 i i i 个位置上已经有数据了(除非 i = = l e n ( n u m s ) i == len(nums) i==len(nums)),要把第 i ∼ l e n ( n u m s ) − 1 i \sim len(nums) - 1 i∼len(nums)−1 位置上的元素依次向后移动。
- 然后再在第 i i i 个元素位置赋值为 v a l val val,并更新数组的元素计数值。
Python 中的 list 列表直接封装了中间插入操作,直接调用 insert 方法即可。
arr = [0, 5, 2, 3, 7, 1, 6]
i, val = 2, 4
arr.insert(i, val)
print(arr)
「在数组中间位置插入元素」的操作中,由于移动元素的操作次数跟元素个数有关,因此,「在数组中间位置插入元素」的最坏和平均时间复杂度都是 O ( n ) O(n) O(n)。
2.4 改变元素
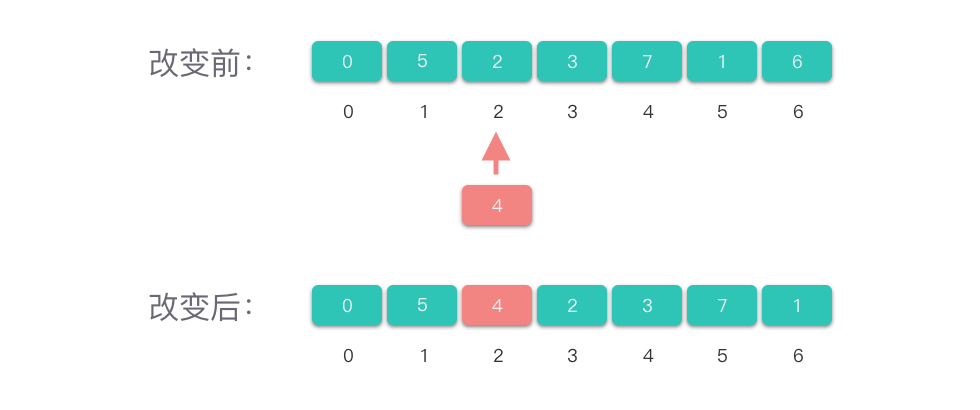
将数组中第 i i i 个元素值改为 v a l val val:
- 需要先检查 i i i 的范围是否在合法的范围区间,即 0 ≤ i ≤ l e n ( n u m s ) − 1 0 \le i \le len(nums) - 1 0≤i≤len(nums)−1。
- 然后将第 i i i 个元素值赋值为 v a l val val。
def change(nums, i, val):
if 0 <= i <= len(nums) - 1:
nums[i] = val
arr = [0, 5, 2, 3, 7, 1, 6]
i, val = 2, 4
change(arr, i, val)
print(arr)
「改变元素」的操作跟访问元素操作类似,访问操作不依赖于数组中元素个数,因此,「改变元素」的时间复杂度为 O ( 1 ) O(1) O(1)。
2.5 删除元素
删除元素分为三种情况:「删除数组尾部元素」、「删除数组第 i i i 个位置上的元素」、「基于条件删除元素」。
删除数组尾部元素:
- 只需将元素计数值减一即可。
Python 中的 list 列表直接封装了删除数组尾部元素的操作,只需要调用 pop 方法即可。
arr = [0, 5, 2, 3, 7, 1, 6]
arr.pop()
print(arr)
「删除数组尾部元素」的操作,不依赖于数组中的元素个数,因此,「删除数组尾部元素」的时间复杂度为 O ( 1 ) O(1) O(1)。
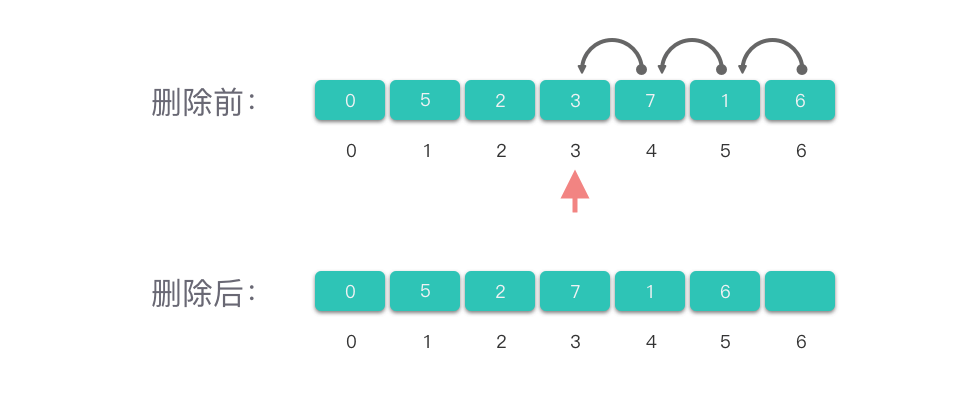
删除数组第 i i i 个位置上的元素:
- 先检查下标 i i i 是否合法,即 0 ≤ i ≤ l e n ( n u m s ) − 1 0 \le i \le len(nums) - 1 0≤i≤len(nums)−1。
- 如果下标合法,则将第 i + 1 i + 1 i+1 个位置到第 l e n ( n u m s ) − 1 len(nums) - 1 len(nums)−1 位置上的元素依次向左移动。
- 删除后修改数组的元素计数值。
Python 中的 list 列表直接封装了删除数组中间元素的操作,只需要以下标作为参数调用 pop 方法即可。
arr = [0, 5, 2, 3, 7, 1, 6]
i = 3
arr.pop(i)
print(arr)
「删除数组中间位置元素」的操作同样涉及移动元素,而移动元素的操作次数跟元素个数有关,因此,「删除数组中间位置元素」的最坏和平均时间复杂度都是 O ( n ) O(n) O(n)。
基于条件删除元素:这种操作一般不给定被删元素的位置,而是给出一个条件要求删除满足这个条件的(一个、多个或所有)元素。这类操作也是通过循环检查元素,查找到元素后将其删除。
arr = [0, 5, 2, 3, 7, 1, 6]
arr.remove(5)
print(arr)
「基于条件删除元素」的操作同样涉及移动元素,而移动元素的操作次数跟元素个数有关,因此,「基于条件删除元素」的最坏和平均时间复杂度都是 O ( n ) O(n) O(n)。
到这里,有关数组的基础知识就介绍完了。下面进行一下总结。
3. 数组的基础知识总结
数组是最基础、最简单的数据结构。数组是实现线性表的顺序结构存储的基础。它使用一组连续的内存空间,来存储一组具有相同类型的数据。
数组的最大特点的支持随机访问。访问数组元素、改变数组元素的时间复杂度为 O ( 1 ) O(1) O(1),在数组尾部插入、删除元素的时间复杂度也是 O ( 1 ) O(1) O(1),普通情况下插入、删除元素的时间复杂度为 O ( n ) O(n) O(n)。
二. 数组基础知识题目
数组操作题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0189 | 轮转数组 | 网页链接、Github 链接 | 数组、数学、双指针 | 中等 |
| 0066 | 加一 | 网页链接、Github 链接 | 数组、数学 | 简单 |
| 0724 | 寻找数组的中心下标 | 网页链接、Github 链接 | 数组、前缀和 | 简单 |
| 0485 | 最大连续 1 的个数 | 数组 | 简单 | |
| 0238 | 除自身以外数组的乘积 | 数组、前缀和 | 中等 |
二维数组题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0498 | 对角线遍历 | 网页链接、Github 链接 | 数组、矩阵、模拟 | 中等 |
| 0048 | 旋转图像 | 网页链接、Github 链接 | 数组、数学、矩阵 | 中等 |
| 0073 | 矩阵置零 | 数组、哈希表、矩阵 | 中等 | |
| 0054 | 螺旋矩阵 | 网页链接、Github 链接 | 数组、矩阵、模拟 | 中等 |
| 0059 | 螺旋矩阵 II | 数组、矩阵、模拟 | 中等 | |
| 0289 | 生命游戏 | 数组、矩阵、模拟 | 中等 |
三. 练习题目
1. 0066. 加一
1.1 题目大意
描述:给定一个非负整数数组,数组每一位对应整数的一位数字。
要求:计算整数加 1 后的结果。
说明:
- 1 ≤ d i g i t s . l e n g t h ≤ 100 1 \le digits.length \le 100 1≤digits.length≤100。
- 0 ≤ d i g i t s [ i ] ≤ 9 0 \le digits[i] \le 9 0≤digits[i]≤9。
示例:
输入:digits = [1,2,3]
输出:[1,2,4]
解释:输入数组表示数字 123,加 1 之后为 124。
1.2 解题思路
思路 1:模拟
这道题把整个数组看成了一个整数,然后个位数加 1。问题的实质是利用数组模拟加法运算。
如果个位数不为 9 的话,直接把个位数加 1 就好。如果个位数为 9 的话,还要考虑进位。
具体步骤:
- 逆序遍历数组
- 如果该位数字不为
9,则将该位数字加1,完成加1运算直接返回数组。 - 如果该位数字为
9,则将该位数字置为0, 即加1后10的个位数, 此时将该位数字排除, 又转化为剩下的数字加1。 - 直到遍历完整个数组, 如果依旧没有遇到不为
9的数字, 则在数组前补1
- 如果该位数字不为
思路 1:代码
class Solution:
def plusOne(self, digits: List[int]) -> List[int]:
for i in range(len(digits) - 1, -1, -1):
if digits[i] - 9:
digits[i] += 1
return digits
digits[i] = 0
return [1] + digits
思路 1:复杂度分析
- 时间复杂度: O ( n ) O(n) O(n)。一重循环遍历的时间复杂度为 O ( n ) O(n) O(n) 。
- 空间复杂度: O ( 1 ) O(1) O(1)。
2. 0724. 寻找数组的中心下标
2.1 题目大意
描述:给定一个数组 nums。
要求:找到「左侧元素和」与「右侧元素和相等」的位置,若找不到,则返回 -1。
说明:
- 1 ≤ n u m s . l e n g t h ≤ 1 0 4 1 \le nums.length \le 10^4 1≤nums.length≤104。
- − 1000 ≤ n u m s [ i ] ≤ 1000 -1000 \le nums[i] \le 1000 −1000≤nums[i]≤1000。
示例:
输入:nums = [1, 7, 3, 6, 5, 6]
输出:3
解释
中心下标是 3 。
左侧数之和 sum = nums[0] + nums[1] + nums[2] = 1 + 7 + 3 = 11 ,
右侧数之和 sum = nums[4] + nums[5] = 5 + 6 = 11 ,二者相等。
2.2 解题思路
思路 1:两次遍历
两次遍历,第一次遍历先求出数组全部元素和。第二次遍历找到左侧元素和恰好为全部元素和一半的位置。
思路 1:代码
class Solution:
def pivotIndex(self, nums: List[int]) -> int:
t, s = sum(nums), 0
for i in range(len(nums)):
if not s * 2 + nums[i] -t: return i
s += nums[i]
return -1
思路 1:复杂度分析
- 时间复杂度: O ( n ) O(n) O(n)。两次遍历的时间复杂度为 O ( 2 ∗ n ) O(2 * n) O(2∗n) , O ( 2 ∗ n ) = = O ( n ) O(2 * n) == O(n) O(2∗n)==O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
3. 0189. 轮转数组
3.1 题目大意
描述:给定一个数组 nums,再给定一个数字 k。
要求:将数组中的元素向右移动 k 个位置。
说明:
- 1 ≤ n u m s . l e n g t h ≤ 1 0 5 1 \le nums.length \le 10^5 1≤nums.length≤105。
- − 2 31 ≤ n u m s [ i ] ≤ 2 31 − 1 -2^{31} \le nums[i] \le 2^{31} - 1 −231≤nums[i]≤231−1。
- 0 ≤ k ≤ 1 0 5 0 \le k \le 10^5 0≤k≤105。
- 使用空间复杂度为
O(1)的原地算法解决这个问题。
示例:
输入:nums = [1,2,3,4,5,6,7], k = 3
输出:[5,6,7,1,2,3,4]
解释
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
3.2 解题思路
思路 1:环状交换
从位置 0 0 0 开始,最初令 t e m p = n u m s [ 0 ] temp=nums[0] temp=nums[0]。根据规则,位置 0 0 0的元素会放至 ( 0 + k ) m o d n (0+k) mod n (0+k)modn的位置,令 x = ( 0 + k ) m o d x x = (0+k) mod x x=(0+k)modx,此时交换 t e m p temp temp 和 n u m s [ x ] nums[x] nums[x],完成位置 x x x 的更新。然后,我们考察位置 x x x,并交换 t e m p temp temp和 n u m s [ ( x + k ) m o d n ] nums[(x+k) mod n] nums[(x+k)modn],从而完成下一个位置的更新。不断进行上述过程,直至回到初始位置 0 0 0。
容易发现,当回到初始位置 0 0 0 时,有些数字可能还没有遍历到,此时我们应该从下一个数字开始重复的过程,可是这个时候怎么才算遍历结束呢?我们不妨先考虑这样一个问题:从 0 0 0 开始不断遍历,最终回到起点 0 0 0 的过程中,我们遍历了多少个元素?
由于最终回到了起点,故该过程恰好走了整数数量的圈,不妨设为 a a a 圈;再设该过程总共遍历了 b b b 个元素。因此,我们有 a n = b k an = bk an=bk,即 a n an an 一定为 n , k n,k n,k 的公倍数。又因为我们在第一次回到起点时就结束,因此 a a a要尽可能小,故 a n an an 就是 n , k n,k n,k 的最小公倍数 l c m ( n , k ) lcm(n,k) lcm(n,k),因此 b b b 就为 l c m ( n , k ) / k lcm(n,k)/k lcm(n,k)/k。
这说明单次遍历会访问到 l c m ( n , k ) / k lcm(n,k)/k lcm(n,k)/k 个元素。为了访问到所有的元素,我们需要进行遍历的次数为
n l c m ( n , k ) / k = n k l c m ( n , k ) = g c d ( n , k ) \frac{n}{lcm(n,k)/k} = \frac{nk}{lcm(n,k)} = gcd(n,k) lcm(n,k)/kn=lcm(n,k)nk=gcd(n,k)
其中 g c d gcd gcd 指的是最大公约数。
思路 1:代码
from math import gcd
class Solution:
def rotate(self, nums: List[int], k: int) -> None:
n = len(nums)
k, c = k % n, gcd(k, n)
for i in range(c):
for j in range(n // c + 3):
l = (i + j * k) % n
r = (i + k) % n
nums[l], nums[r] = nums[r], nums[l]
return nums
思路 1:复杂度分析
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
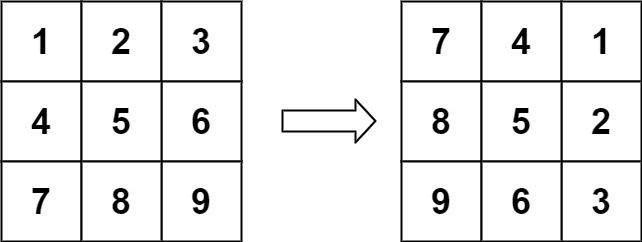
4. 0048. 旋转图像
4.1 题目大意
描述:给定一个 n * n 大小的二维矩阵(代表图像)matrix。
要求:将二维矩阵 matrix 顺时针旋转 90°。
说明:
- 不能使用额外的数组空间。
- n = = m a t r i x . l e n g t h = = m a t r i x [ i ] . l e n g t h n == matrix.length == matrix[i].length n==matrix.length==matrix[i].length。
- 1 ≤ n ≤ 20 1 \le n \le 20 1≤n≤20。
- − 1000 ≤ m a t r i x [ i ] [ j ] ≤ 1000 -1000 \le matrix[i][j] \le 1000 −1000≤matrix[i][j]≤1000。
示例:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[[7,4,1],[8,5,2],[9,6,3]]
输入:matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出:[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
4.2 解题思路
思路 1:原地旋转
如果使用额外数组空间的话,将对应元素存放到对应位置即可。如果不使用额外的数组空间,则需要观察每一个位置上的点最初位置和最终位置有什么规律。
对于矩阵中第 i 行的第 j 个元素,在旋转后,它出现在倒数第 i 列的第 j 个位置。即 matrixnew[j][n − i − 1] = matrix[i][j]。
而 matrixnew[j][n - i - 1] 的点经过旋转移动到了 matrix[n − i − 1][n − j − 1] 的位置。
matrix[n − i − 1][n − j − 1] 位置上的点经过旋转移动到了 matrix[n − j − 1][i] 的位置。
matrix[n− j − 1][i] 位置上的点经过旋转移动到了最初的 matrix[i][j] 的位置。
这样就形成了一个循环,我们只需要通过一个临时变量 temp 就可以将循环中的元素逐一进行交换。Python 中则可以直接使用语法直接交换。
思路 1:代码
class Solution:
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
for i in range(n // 2):
for j in range((n + 1) // 2):
matrix[i][j], matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1] = matrix[n - j - 1][i], matrix[n - i - 1][n - j - 1], matrix[j][n - i - 1], matrix[i][j]
思路 1:复杂度分析
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
思路 2:原地翻转
通过观察可以得出:原矩阵可以通过一次「水平翻转」+「主对角线翻转」得到旋转后的二维矩阵。
思路 2:代码
def rotate(self, matrix: List[List[int]]) -> None:
n = len(matrix)
for i in range(n // 2):
for j in range(n):
matrix[i][j], matrix[n - i - 1][j] = matrix[n - i - 1][j], matrix[i][j]
for i in range(n):
for j in range(i):
matrix[i][j], matrix[j][i] = matrix[j][i], matrix[i][j]
思路 2:复杂度分析
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
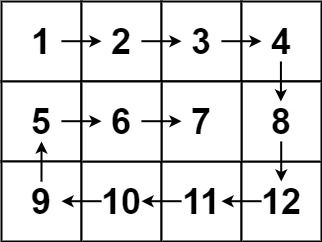
5. 0054. 螺旋矩阵
5.1 题目大意
描述:给定一个 m * n 大小的二维矩阵 matrix。
要求:按照顺时针旋转的顺序,返回矩阵中的所有元素。
说明:
- m = = m a t r i x . l e n g t h m == matrix.length m==matrix.length。
- n = = m a t r i x [ i ] . l e n g t h n == matrix[i].length n==matrix[i].length。
- 1 ≤ m , n ≤ 10 1 \le m, n \le 10 1≤m,n≤10。
- − 100 ≤ m a t r i x [ i ] [ j ] ≤ 100 -100 \le matrix[i][j] \le 100 −100≤matrix[i][j]≤100。
示例:
输入:matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,3,6,9,8,7,4,5]
输入:matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
输出:[1,2,3,4,8,12,11,10,9,5,6,7]
5.2 解题思路
思路 1:模拟
- 使用数组
ans存储答案。然后定义一下上、下、左、右的边界。 - 然后按照逆时针的顺序从边界上依次访问元素。
- 当访问完当前边界之后,要更新一下边界位置,缩小范围,方便下一轮进行访问。
- 最后返回答案数组
ans。
思路 1:代码
class Solution:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
up, down, left, right = 0, len(matrix)-1, 0, len(matrix[0])-1
ans = []
while True:
for i in range(left, right + 1):
ans.append(matrix[up][i])
up += 1
if up > down:
break
for i in range(up, down + 1):
ans.append(matrix[i][right])
right -= 1
if right < left:
break
for i in range(right, left - 1, -1):
ans.append(matrix[down][i])
down -= 1
if down < up:
break
for i in range(down, up - 1, -1):
ans.append(matrix[i][left])
left += 1
if left > right:
break
return ans
思路 1:复杂度分析
- 时间复杂度: O ( m ∗ n ) O(m * n) O(m∗n)。其中 m m m、 n n n 分别为二维矩阵的行数和列数。
- 空间复杂度: O ( m ∗ n ) O(m * n) O(m∗n)。如果算上答案数组的空间占用,则空间复杂度为 O ( m ∗ n ) O(m * n) O(m∗n)。不算上则空间复杂度为 O ( 1 ) O(1) O(1)。
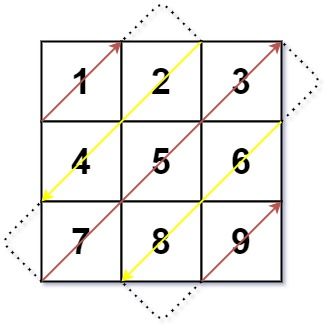
6. 0498. 对角线遍历
6.1 题目大意
描述:给定一个大小为 m * n 的矩阵 mat 。
要求:以对角线遍历的顺序,用一个数组返回这个矩阵中的所有元素。
说明:
- m = = m a t . l e n g t h m == mat.length m==mat.length。
- n = = m a t [ i ] . l e n g t h n == mat[i].length n==mat[i].length。
- 1 ≤ m , n ≤ 1 0 4 1 \le m, n \le 10^4 1≤m,n≤104。
- 1 ≤ m ∗ n ≤ 1 0 4 1 \le m * n \le 10^4 1≤m∗n≤104。
- − 1 0 5 ≤ m a t [ i ] [ j ] ≤ 1 0 5 -10^5 \le mat[i][j] \le 10^5 −105≤mat[i][j]≤105。
示例:
输入:mat = [[1,2,3],[4,5,6],[7,8,9]]
输出:[1,2,4,7,5,3,6,8,9]
6.2 解题思路
思路 1:找规律 + 考虑边界问题
这道题的关键是「找规律」和「考虑边界问题」。
找规律:
- 当「行号 + 列号」为偶数时,遍历方向为从左下到右上。可以记为右上方向
(-1, +1),即行号减1,列号加1。 - 当「行号 + 列号」为奇数时,遍历方向为从右上到左下。可以记为左下方向
(+1, -1),即行号加1,列号减1。
边界情况:
- 向右上方向移动时:
- 如果在最后一列,则向下方移动,即
x += 1。 - 如果在第一行,则向右方移动,即
y += 1。 - 其余情况想右上方向移动,即
x -= 1、y += 1。
- 如果在最后一列,则向下方移动,即
- 向左下方向移动时:
- 如果在最后一行,则向右方移动,即
y += 1。 - 如果在第一列,则向下方移动,即
x += 1。 - 其余情况向左下方向移动,即
x += 1、y -= 1。
- 如果在最后一行,则向右方移动,即
思路 1:代码
class Solution:
def findDiagonalOrder(self, mat: List[List[int]]) -> List[int]:
rows = len(mat)
cols = len(mat[0])
count = rows * cols
x, y = 0, 0
ans = []
for i in range(count):
ans.append(mat[x][y])
if (x + y) % 2 == 0:
# 最后一列
if y == cols - 1:
x += 1
# 第一行
elif x == 0:
y += 1
# 右上方向
else:
x -= 1
y += 1
else:
# 最后一行
if x == rows - 1:
y += 1
# 第一列
elif y == 0:
x += 1
# 左下方向
else:
x += 1
y -= 1
return ans
思路 1:复杂度分析
- 时间复杂度: O ( m × n ) O(m \times n) O(m×n)。其中 m m m、 n n n 分别为二维矩阵的行数、列数。
- 空间复杂度: O ( m ∗ n ) O(m * n) O(m∗n)。如果算上答案数组的空间占用,则空间复杂度为 O ( m ∗ n ) O(m * n) O(m∗n)。不算上则空间复杂度为 O ( 1 ) O(1) O(1)。