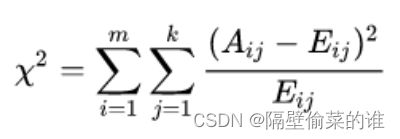数据预处理-分箱（Binning）和 WOE编码
数据预处理-分箱（Binning）和 WOE编码
1. 分箱
1.1 理论
1.1.1 定义 分箱就是将连续的特征离散化，以某种方式将特征值映射到几个箱(bin)中。
1.1.2 为什么要进行分箱？
- 引入非线性变换，增强模型性能。因为原始值和目标值之间可能并不存在线性关系，所以直接使用模型预测起不到很好的效果。
- 增强模型可解释性。通过分箱可以得到一个分段函数，模型可解释性更强。
- 对异常值不敏感，增强模型鲁棒性，防止过拟合。异常值终也会被分到一个箱里面，不会影响其他箱内正常特征值，分箱的在一定程度上也可以防止过拟合。
- 重要的是分箱之后我们还可以对不同的箱做进一步的统计和特征组合。比如WOE编码。
1.1.3 常用分箱方法：
- 卡方分箱（最稳定，最常用）
卡方值计算公式：
其中：
m: 箱的数量；
k: 类别数量；
Aij: 第i个箱第j类中样本数量（频数）;
Eij: 如果箱的划分和类别独立同分布，第i个箱第j类中样本数量的期望值（频数）；设箱的划分和类别独立同分布，则样本同时在第i个箱第j类中的概率为：pij = pi * pj，同时在第i个箱第j类中的有样本数量期望值为：pij * N 。
卡方值计算的例子，设m=2, k=2，
表1 实际频数
| 类别1 | 类别2 | 行和 | |
|---|---|---|---|
| 箱1 | A11 | A12 | R1 |
| 箱2 | A21 | A22 | R2 |
| 列和 | C1 | C2 |
表2 期望频数（Eij）
| 类别1 | 类别2 | |
|---|---|---|
| 箱1 | E11 = pi * pj * N =(R1 /N) * (C1 / N) * N = R1 * C1 / N | E12 = R1 * C2 / N |
| 箱2 | E21 = R2 * C1 / N | E22 = R2 * C2 / N |
表1和表2中的数据带入卡方值计算公式，即可求出箱1和箱2合并的卡方值。卡方值越小，说明真实值与期望值越接近，箱的划分和类别越接近独立同分布（类的划分和箱的划分没有关系），那么两个箱具有相同的标签分布，可以合并。
卡方检验步骤：
（1）初始化：根据连续变量值大小进行排序，构建最初的离散化，即把每一个单独的值视为一个箱体。这样做的目的是从每个单独的个体开始逐渐合并。
（2）合并：遍历相邻两项合并的卡方值，将卡方值最小的两组合并，不断重复直到满足分箱数目的限制。决策树分箱
-
聚类分箱
使用k-means进行聚类分箱，算法比较简单，不再详细说：先初始化k个类中心，每一次迭代将样本划分到最近的类中，然后修正类中心，直到类中心不再发生变化，停止迭代。
-
等频分箱
每一个箱中的样本数相同，实现很简单，先排序，按顺序放到对应的箱中即可。
-
等距分箱
箱的大小相同，例如年龄分箱：0-5岁，5-10岁，10-15岁，…
-
决策树分箱
将某一列数据作为训练集，将label作为结果，直接训练一个决策树，然后根据决策树的分裂节点的阈值作为分箱的依据。
1.1.4 实验
- 这个实验使用toad库（https://toad.readthedocs.io/en/stable/tutorial_chinese.html）来做分箱。
- 数据集使用（https://archive.ics.uci.edu/dataset/350/default+of+credit+card+clients），数据集介绍：
UCI数据集包含30,000名客户及其在台湾一家银行的信用卡交易数据。除了客户的静态特征外，该数据集还包含某年4月至9月的信用卡账单支付历史，以及客户信用卡的余额限制。目标是客户是否会在接下来的一个月，即该年10月拖欠信用卡付款。可以想象，在这个数据上训练出来的模型在实践中可以用来确定客户是否有资格获得其他产品，如汽车贷款等。该数据集包含23个输入变量(input variable)和一个响应变量（response variable）。该数据集来源于UCI machine learning repository,为某银行的信用卡客户信息数据，共有30000个样本，包括过去六个月的账单还款情况。
ID：信用卡客户ID号
LIMIT_BAL：以新台币计算的信贷金额（包括个人和家庭/补充信贷）/ 信用卡限额，会被替换成一个合成的更具典型性的特征。
SEX： 性别 (1代表男性，2代表女性)
EDUCATION：受 教育程度(1=研究生, 2=大学, 3=高中, 4=其他 5=未知, 6=未知)
MARRIAGE：婚姻状况（1=已婚，2=单身，3=其他）
AGE：年龄
X1：信用额度，包括其个人和家庭补充信用
X2：性别（1=male;2=female）
X3：教育（1=研究生，2=大学，3=高中，4=其他）
X4：婚姻状况（1=已婚，2=单身，3=其他）
X5：年龄，age
X6-X11：过去六个月的还款情况。其中，-1,代表按时还款；1,代表延时一个月还款；2,代表延时两个月还款…依次类推，XN=n,代表延时n个月还款，
X12-X17：过去六个月的账单数额情况。
X18-X23：过去六个月的还款数额情况。
Y：目标属性，客户下个月还款违约情况（1=逾期，0=未逾期）
# 导入数据集
import os
import eda
import pandas as pd
import numpy as np
import toad
data_dir = "./"
df = pd.read_csv(os.path.join(data_dir, "default_of_credit_card_clients.csv"))
df["SEX"] = df["SEX"].map({1: "男", 2: "女"})
df["EDUCATION"] = df["EDUCATION"].map({1: "研究生", 2: "大学", 3: "高中", 4: "其他", 5: "未知", 6: "未知"})
df["MARRIAGE"] = df["MARRIAGE"].map({1: "已婚", 2: "单身", 3: "其他"})
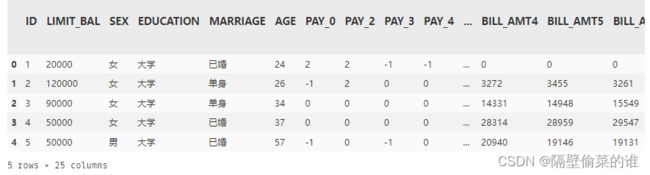
df.head()
# 分箱，并查看分箱结果
X = df.drop(["ID", "default payment next month"], axis=1)
y = df["default payment next month"]
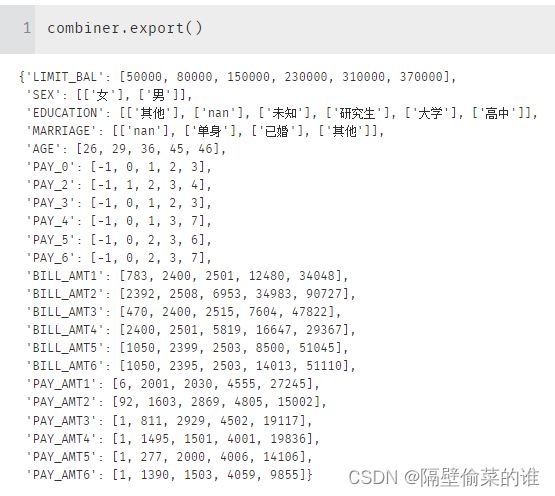
combiner = toad.transform.Combiner()
combiner.fit(X, y, method='chi', n_bins=6, min_samples=0.05, exclude=[])
# 查看分箱后的数据数据分布，使用了卡方分箱和决策树分箱
from toad.plot import bin_plot
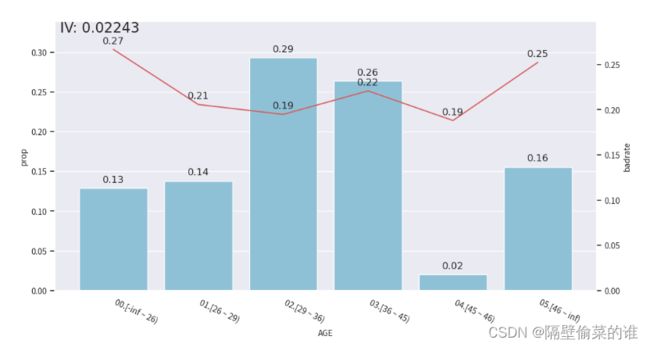
for method in ['chi', 'dt']:
c = combiner.fit(X[["AGE"]], y, method=method, n_bins=6, min_samples=0.05)
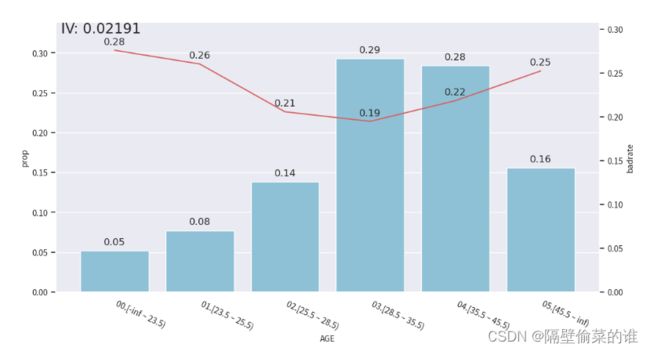
bin_plot(c.transform(df, labels=True), x='AGE', target="default payment next month")
在图中，蓝色bar代表了样本量占比，红线代表了正样本占比（e.g. 坏账率），也就是target的汇总。
2.WOE编码
WOE(Weight of Evidence)，证据权重，它是一种对原始自变量有标准化功能的编码形式。WOE编码的定义为：
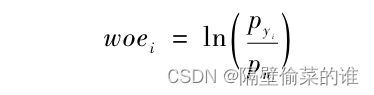
其中，pyi是当前分组中响应客户占样本中所有响应客户的比例，pni是当前分组中未响应客户占样本中所有未响应客户的比例，而WOE表示的实际上是二者之间的差异。WOE也可以理解为，当前组中响应的客户和未响应客户的比值与所有样本中这个比值的差异。这个差异是通过对这两个比值取对数来表示的。WOE越大，差异越大，这个分组里的样本响应的可能性就越大；WOE越小，差异越小，这个分组里的样本响应的可能性也就越小。
用调整好的Combiner（分箱器）进行WOE转化
t = toad.transform.WOETransformer()
tt = 'default payment next month'
woe = t.fit_transform(c.transform(df[["AGE", tt]]), df[tt], exclude=[tt])
woe.head()
