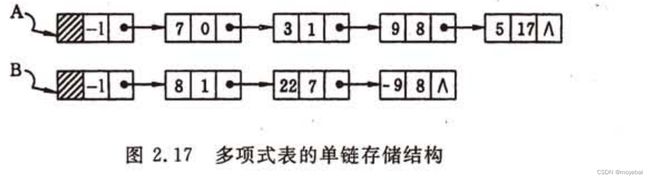
第 2 章 线性表(抽象数据类型 Polynomial 的实现)
1. 背景说明
2. 示例代码
1) status.h
/* DataStructure 预定义常量和类型头文件 */
#ifndef STATUS_H
#define STATUS_H
#define CHECK_NULL(pointer) if (!(pointer)) { \
printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_NULL_PTR); \
return NULL; \
}
#define CHECK_RET(ret) if (ret != RET_OK) { \
printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ret); \
return ret; \
}
#define CHECK_VALUE(value, ERR_CODE) if (value) { \
printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_CODE); \
return ERR_CODE; \
}
#define CHECK_FALSE(value, ERR_CODE) if (!(value)) { \
printf("FuncName: %-15s Line: %-5d ErrorCode: %-3d\n", __func__, __LINE__, ERR_CODE); \
return FALSE; \
}
/* 函数结果状态码 */
#define TRUE 1 /* 返回值为真 */
#define FALSE 0 /* 返回值为假 */
#define RET_OK 0 /* 返回值正确 */
#define INFEASIABLE 2 /* 返回值未知 */
#define ERR_MEMORY 3 /* 访问内存错 */
#define ERR_NULL_PTR 4 /* 空指针错误 */
#define ERR_MEMORY_ALLOCATE 5 /* 内存分配错 */
#define ERR_NULL_STACK 6 /* 栈元素为空 */
#define ERR_PARA 7 /* 函数参数错 */
#define ERR_OPEN_FILE 8 /* 打开文件错 */
#define ERR_NULL_QUEUE 9 /* 队列为空错 */
#define ERR_FULL_QUEUE 10 /* 队列为满错 */
#define ERR_NOT_FOUND 11 /* 表项不存在 */
typedef int Status; /* Status 是函数的类型,其值是函数结果状态代码,如 RET_OK 等 */
typedef int Bollean; /* Boolean 是布尔类型,其值是 TRUE 或 FALSE */
#endif // !STATUS_H
2) linkList.h
/* 具有实用意义的线性链表(带头结点)实现头文件 */
#ifndef LINKLIST_H
#define LINKLIST_H
#include "status.h"
typedef struct {
float coef; /* 系数 */
int expn; /* 指数 */
} Term, ElemType;
typedef struct LNode {
ElemType data;
struct LNode *next;
} LNode, *Link, *Position;
typedef struct LinkList {
Link head;
Link tail;
int length;
} LinkList;
typedef LinkList Polynomial;
/* 分配由指向的值为 e 的结点,并返回 OK;若分配失败, 则返回 NULL */
Link MakeNewLNode(ElemType e);
/* 释放 p 所指结点 */
void FreeLNode(Link *p);
/* 构造一个空的线性链表 */
Status InitList(LinkList *L);
/* 将线性链表 L 重置为空表,并释放原链表的结点空间 */
Status ClearList(LinkList *L);
/* 销毁线性链表 L,L 不再存在 */
Status DestroyList(LinkList *L);
/* h 指向 L 的一个结点,把 head 当做头结点,将 s 所指结点插入在第一个结点之前 */
Status InsFirst(LinkList *L, Link head, Link s);
/* h 指向 L 的一个结点,把 h 当做头结点,删除链表中的第一个结点并以 q 返回
若链表为空( h 指向尾结点),q = NULL,返回 FALSE */
Status DelFirst(LinkList *L, Link head, Link *q);
/* 将指针 s(s->data 为第一个数据元素)所指(彼此以指针相链,以 NULL 结尾)的一
串结点链接在线性链表L的最后一个结点之后,并改变链表 L 的尾指针指向新的尾结点 */
Status Append(LinkList *L, Link s);
/* 已知 p 指向线性链表 L 中的一个结点,返回 p 所指结点的直接前驱的位置若无前驱
则返回 NULL */
Position PriorPos(LinkList L, Link p);
/* 删除线性链表 L 中的尾结点并以 q 返回,改变链表 L 的尾指针指向新的尾结点 */
Bollean Remove(LinkList *L, Link *q);
/* 已知 *p 指向线性链表 L 中的一个结点,将 s 所指结点插入在 *p 所指结点之前
并修改指针 p 指向新插入的结点 */
Status InsBefore(LinkList *L, Link *p, Link s);
/* 已知 *p 指向线性链表 L 中的一个结点,将 s 所指结点插入在 *p 所指结点之后
并修改指针 p 指向新插入的结点 */
Status InsAfter(LinkList *L, Link *p, Link s);
/* 已知 p 指向线性链表中的一个结点,用 e 更新 p 所指结点中数据元素的值 */
Status SetCurrElem(Link p, ElemType e);
/* 已知 p 指向线性链表中的一个结点,返回 p 所指结点中数据元素的值 */
ElemType GetCurrElem(Link p);
/* 若线性链表 L 为空表,则返回 TRUE,否则返回 FALSE */
Bollean ListEmpty(LinkList L);
/* 返回线性链表 L 中元素个数 */
int ListLength(LinkList L);
/* 返回线性链表 L 中头结点的位置 */
Position GetHead(LinkList L);
/* 返回线性链表 L 中最后一个结点的位置 */
Position GetLast(LinkList L);
/* 已知 p 指向线性链表 L 中的一个结点,返回 p 所指结点的直接后继的位置
若无后继,则返回 NULL */
Position NextPos(Link p);
/* 返回 p 指示线性链表 L 中第 i 个结点的位置,并返回 OK,i 值不合法时
返回 ERROR, i = 0 为头结点 */
Status LocatePos(LinkList L, int i, Link *p);
/* 返回线性链表 L 中第 1 个与 e 满足函数 compare() 判定关系的元素的位
置若不存在这样的元素,则返回 NULL */
Position LocateElem(LinkList L, ElemType e, Bollean(*compare)(ElemType, ElemType));
/* 依次对 L 的每个数据元素调用函数 visit()。一旦 visit() 失败,则操作失败 */
Status ListTraverse(LinkList L, void(*visit)(ElemType));
/* 已知 L 为有序线性链表,将元素 e 按非降序插入在 L 中 */
Status InsertAscend(LinkList *L, ElemType e, int(*compare)(ElemType, ElemType));
/* 若升序链表 L 中存在与 e 满足判定函数 compare() 取值为 0 的元素,则 q 指示 L 中
第一个值为 e 的结点的位置,并返回 TRUE;否则 q 指示第一个与 e 满足判定函数
compare() 取值 > 0 的元素的前驱的位置, 并返回 FALSE */
Bollean LocateElemP(LinkList L, ElemType e, Position *q, int(*compare)(ElemType, ElemType));
#endif // !LINKLIST_H3) linkList.c
/* 具有实用意义的线性链表(带头结点)实现源文件 */
#include "linkList.h"
#include
#include
/* 分配由指向的值为 e 的结点,并返回 OK;若分配失败, 则返回 NULL */
Link MakeNewLNode(ElemType e)
{
Link newLNode = (Link)malloc(sizeof(LNode));
CHECK_NULL(newLNode)
newLNode->data = e;
newLNode->next = NULL;
return newLNode;
}
/* 释放 p 所指结点 */
void FreeLNode(Link *p)
{
free(*p);
*p = NULL;
}
/* 构造一个空的线性链表 */
Status InitList(LinkList *L)
{
Link p = (Link)malloc(sizeof(LNode));
CHECK_VALUE(!p, ERR_MEMORY_ALLOCATE)
p->next = NULL;
(*L).head = (*L).tail = p;
(*L).length = 0;
return RET_OK;
}
/* 将线性链表 L 重置为空表,并释放原链表的结点空间 */
Status ClearList(LinkList *L)
{
CHECK_VALUE(!L, ERR_NULL_PTR)
if ((*L).head == (*L).tail) {
return RET_OK;
}
Link p, q;
p = (*L).head->next;
(*L).head->next = NULL;
while (p != (*L).tail) {
q = p;
p = p->next;
free(q);
}
free(p);
(*L).tail = (*L).head;
(*L).length = 0;
return RET_OK;
}
/* 销毁线性链表 L,L 不再存在 */
Status DestroyList(LinkList *L)
{
ClearList(L);
FreeLNode(&((*L).head));
(*L).tail = NULL;
return RET_OK;
}
/* h 指向 L 的一个结点,把 head 当做头结点,将 s 所指结点插入在第一个结点之前 */
Status InsFirst(LinkList *L, Link head, Link s)
{
s->next = head->next;
head->next = s;
if (head == (*L).tail) {
(*L).tail = head->next;
}
++((*L).length);
return RET_OK;
}
/* h 指向 L 的一个结点,把 h 当做头结点,删除链表中的第一个结点并以 q 返回
若链表为空( h 指向尾结点),q = NULL,返回 FALSE */
Status DelFirst(LinkList *L, Link head, Link *q)
{
*q = head->next;
if (!(*q)) {
return FALSE;
}
head->next = (*q)->next;
if (!(head->next)) {
(*L).tail = head;
}
--(*L).length;
return RET_OK;
}
/* 将指针 s(s->data 为第一个数据元素)所指(彼此以指针相链,以 NULL 结尾)的一
串结点链接在线性链表L的最后一个结点之后,并改变链表 L 的尾指针指向新的尾结点 */
Status Append(LinkList *L, Link s)
{
int length = 1;
(*L).tail->next = s;
while (s->next) {
++length;
s = s->next;
}
(*L).tail = s;
(*L).length += length;
return RET_OK;
}
/* 已知 p 指向线性链表 L 中的一个结点,返回 p 所指结点的直接前驱的位置若无前驱
则返回 NULL */
Position PriorPos(LinkList L, Link p)
{
Link q = L.head->next;
if (p == q) {
return NULL;
}
while (q->next != p) {
q = q->next;
}
return q;
}
/* 删除线性链表 L 中的尾结点并以 q 返回,改变链表 L 的尾指针指向新的尾结点 */
Bollean Remove(LinkList *L, Link *q)
{
CHECK_VALUE(!L, ERR_NULL_PTR)
if ((*L).length == 0) {
*q = NULL;
return FALSE;
}
Link p = (*L).head;
while (p->next != (*L).tail) {
p = p->next;
}
*q = (*L).tail;
p->next = NULL;
(*L).tail = p;
--((*L).length);
return TRUE;
}
/* 已知 *p 指向线性链表 L 中的一个结点,将 s 所指结点插入在 *p 所指结点之前
并修改指针 *p 指向新插入的结点 */
Status InsBefore(LinkList *L, Link *p, Link s)
{
Link q = PriorPos(*L, *p);
if (!q) {
q = (*L).head;
}
s->next = *p;
q->next = s;
*p = s;
++((*L).length);
return RET_OK;
}
/* 已知 *p 指向线性链表 L 中的一个结点,将 s 所指结点插入在 *p 所指结点之后
并修改指针 p 指向新插入的结点 */
Status InsAfter(LinkList *L, Link *p, Link s)
{
if (*p == (*L).tail) {
(*L).tail = s;
}
s->next = (*p)->next;
(*p)->next = s;
*p = s;
++((*L).length);
return RET_OK;
}
/* 已知 p 指向线性链表中的一个结点,用 e 更新 p 所指结点中数据元素的值 */
Status SetCurrElem(Link p, ElemType e)
{
p->data = e;
return RET_OK;
}
/* 已知 p 指向线性链表中的一个结点,返回 p 所指结点中数据元素的值 */
ElemType GetCurrElem(Link p)
{
return p->data;
}
/* 若线性链表 L 为空表,则返回 TRUE,否则返回 FALSE */
Bollean ListEmpty(LinkList L)
{
return (L.length == 0) ? TRUE : FALSE;
}
/* 返回线性链表 L 中元素个数 */
int ListLength(LinkList L)
{
return L.length;
}
/* 返回线性链表 L 中头结点的位置 */
Position GetHead(LinkList L)
{
return L.head;
}
/* 返回线性链表 L 中最后一个结点的位置 */
Position GetLast(LinkList L)
{
return L.tail;
}
/* 已知 p 指向线性链表 L 中的一个结点,返回 p 所指结点的直接后继的位置
若无后继,则返回 NULL */
Position NextPos(Link p)
{
return p->next;
}
/* 返回 p 指示线性链表 L 中第 i 个结点的位置,并返回 OK,i 值不合法时
返回 ERROR, i = 0 为头结点 */
Status LocatePos(LinkList L, int i, Link *p)
{
CHECK_VALUE((i < 0 || i > L.length), ERR_PARA)
*p = L.head;
for (int j = 0; j < i; ++j) {
*p = (*p)->next;
}
return RET_OK;
}
/* 返回线性链表 L 中第 1 个与 e 满足函数 compare() 判定关系的元素的位
置若不存在这样的元素,则返回 NULL */
Position LocateElem(LinkList L, ElemType e, Bollean(*compare)(ElemType, ElemType))
{
Link p = L.head->next;
while ((p) && !(compare(p->data, e))) {
p = p->next;
}
return p;
}
/* 依次对 L 的每个数据元素调用函数 visit()。一旦 visit() 失败,则操作失败 */
Status ListTraverse(LinkList L, void(*visit)(ElemType))
{
Link p = L.head->next;
for (int i = 0; i < L.length; ++i) {
visit(p->data);
p = p->next;
}
return RET_OK;
}
/* 已知 L 为有序线性链表,将元素 e 按非降序插入在 L 中 */
Status InsertAscend(LinkList *L, ElemType e, int(*compare)(ElemType, ElemType))
{
Link q = (*L).head;
Link p = q->next;
while ((p) && (compare(p->data, e) < 0)) {
q = p;
p = p->next;
}
Link newLNode = MakeNewLNode(e);
q->next = newLNode;
newLNode->next = p;
++((*L).length);
if (!p) {
(*L).tail = newLNode;
}
return RET_OK;
}
/* 若升序链表 L 中存在与 e 满足判定函数 compare() 取值为 0 的元素,则 q 指示 L 中
第一个值为 e 的结点的位置,并返回 TRUE;否则 q 指示第一个与 e 满足判定函数
compare() 取值 > 0 的元素的前驱的位置, 并返回 FALSE */
Bollean LocateElemP(LinkList L, ElemType e, Position *q, int(*compare)(ElemType, ElemType))
{
Link pos = L.head;
Link p = pos->next;
while ((p) && (compare(p->data, e) < 0)) {
pos = p;
p = p->next;
}
if ((!p) || (compare(p->data, e) > 0)) {
*q = pos;
return FALSE;
}
*q = p;
return TRUE;
} 4) algorithm.h
/* 算法定义头文件 */
#ifndef ALGORITHM_H
#define ALGORITHM_H
#include "linkList.h"
/* 算法 2.22, 输入 m 项的系数和指数,建立表示一元多项式的有序链表 P */
Status CreatPolyn(Polynomial *P, int m);
/* 打印输出一元多项式 P */
void PrintPolyn(Polynomial P);
/* 算法 2.23, 多项式加法: Pa = Pa + Pb, 并销毁一元多项式 Pb */
void AddPolyn(Polynomial *Pa, Polynomial *Pb);
/* 算法 2.23, 另一种多项式加法的算法: Pa = Pa + Pb,并销毁一元多项式 Pb */
void AddPolyn2(Polynomial *Pa, Polynomial *Pb);
/* 多项式减法: Pa = Pa - Pb,并销毁一元多项式 Pb */
void SubtractPolyn(Polynomial *Pa, Polynomial *Pb);
/* 多项式乘法: Pa = Pa * Pb,并销毁一元多项式 Pb */
void MultiplyPolyn(Polynomial *Pa, Polynomial *Pb);
#endif // !ALGORITHM_H5) algorithm.c
/* 算法实现源文件 */
#include "algorithm.h"
#include
/* 按有序判定函数 compare() 的约定,将值为 e 的结点插入或合并到升序链表 L 的适当位置 */
Status OrderInsertMerge(LinkList *L, ElemType e, int(*compare)(Term, Term))
{
Position q;
if (LocateElemP(*L, e, &q, compare)) {
q->data.coef += e.coef;
if (!(q->data.coef)) {
Position s = PriorPos(*L, q);
if (!s) {
s = (*L).head;
}
DelFirst(L, s, &q);
FreeLNode(&q);
}
return RET_OK;
}
Link newLNode = MakeNewLNode(e);
CHECK_VALUE(!newLNode, ERR_MEMORY_ALLOCATE)
InsFirst(L, q, newLNode);
return RET_OK;
}
/* 依 a 的指数值 < = 或 > b 的指数值,分别返回 -1 0 或 1 */
int Cmp(Term a, Term b)
{
return (a.expn == b.expn) ? 0 : ((a.expn - b.expn) < 0 ? -1 : 1);
}
/* 算法 2.22, 输入 m 项的系数和指数,建立表示一元多项式的有序链表 P */
Status CreatPolyn(Polynomial *P, int m)
{
CHECK_VALUE(!P, ERR_NULL_PTR)
InitList(P);
printf("Please input %d coefficients and exponents:\n", m);
Term e = { 0 };
Position q;
for (int i = 0; i < m; ++i) {
scanf_s("%f%d", &e.coef, &e.expn);
if (!LocateElemP(*P, e, &q, Cmp)) {
Link newLNode = MakeNewLNode(e);
InsFirst(P, q, newLNode);
}
}
return RET_OK;
}
/* 打印输出一元多项式 P */
void PrintPolyn(Polynomial P)
{
Link q = P.head->next;
printf("%10s%10s\n", "coef", "expo");
while (q) {
printf("%10f%10d\n", q->data.coef, q->data.expn);
q = q->next;
}
}
/* 算法 2.23, 多项式加法: Pa = Pa + Pb, 并销毁一元多项式 Pb */
void AddPolyn(Polynomial *Pa, Polynomial *Pb)
{
Position ha = GetHead(*Pa);
Position hb = GetHead(*Pb);
Position qa = NextPos(ha);
Position qb = NextPos(hb);
while ((!ListEmpty(*Pa)) && (!ListEmpty(*Pb)) && (qa)) {
Term a = GetCurrElem(qa);
Term b = GetCurrElem(qb);
switch (Cmp(a, b)) {
case -1:
ha = qa;
qa = NextPos(ha);
break;
case 0:
qa->data.coef += qb->data.coef;
if (qa->data.coef == 0) {
DelFirst(Pa, ha, &qa);
FreeLNode(&qa);
} else {
ha = qa;
}
DelFirst(Pb, hb, &qb);
FreeLNode(&qb);
qb = NextPos(hb);
qa = NextPos(ha);
break;
case 1:
DelFirst(Pb, hb, &qb);
InsFirst(Pa, ha, qb);
ha = NextPos(ha);
qb = NextPos(hb);
}
}
if (!ListEmpty(*Pb)) {
(*Pb).tail = hb;
Append(Pa, qb);
}
DestroyList(Pb);
}
/* 算法 2.23, 另一种多项式加法的算法: Pa = Pa + Pb,并销毁一元多项式 Pb */
void AddPolyn2(Polynomial *Pa, Polynomial *Pb)
{
Position qb = GetHead(*Pb);
qb = qb->next;
while (qb) {
Term b = GetCurrElem(qb);
OrderInsertMerge(Pa, b, Cmp);
qb = qb->next;
}
DestroyList(Pb);
}
/* 一元多项式系数取反 */
void Opposite(Polynomial Pa)
{
Position p = Pa.head->next;
while (p) {
p->data.coef *= -1;
p = p->next;
}
}
/* 多项式减法: Pa = Pa - Pb,并销毁一元多项式 Pb */
void SubtractPolyn(Polynomial *Pa, Polynomial *Pb)
{
Opposite(*Pb);
AddPolyn(Pa, Pb);
}
/* 多项式乘法: Pa = Pa * Pb,并销毁一元多项式 Pb */
void MultiplyPolyn(Polynomial *Pa, Polynomial *Pb)
{
Polynomial Pc;
InitList(&Pc);
Position qa = GetHead(*Pa)->next;
while (qa) {
Term a = GetCurrElem(qa);
Position qb = GetHead(*Pb)->next;
while (qb) {
Term b = GetCurrElem(qb);
Term c = { 0 };
c.coef = a.coef * b.coef;
c.expn = a.expn + b.expn;
OrderInsertMerge(&Pc, c, Cmp);
qb = qb->next;
}
qa = qa->next;
}
DestroyList(Pb);
ClearList(Pa);
free(Pa->head);
(*Pa).head = Pc.head;
(*Pa).tail = Pc.tail;
(*Pa).length = Pc.length;
} 6) main.c
/* 入口程序源文件 */
#include "algorithm.h"
#include
int main(void)
{
Polynomial p, q;
int m;
printf("Please input the num of the none zero element of p: ");
scanf_s("%d", &m);
CreatPolyn(&p, m);
printf("Please input the num of the none zero element of q: ");
scanf_s("%d", &m);
CreatPolyn(&q, m);
MultiplyPolyn(&p, &q);
printf("The result of add is:\n");
PrintPolyn(p);
DestroyList(&p);
return 0;
} 3. 输出示例(其他均已测试,更换调用接口即可)