Java【归并排序】算法, 大白话式图文解析(附代码)

前言

各位读者好, 我是小陈, 这是我的个人主页
小陈还在持续努力学习编程, 努力通过博客输出所学知识
如果本篇对你有帮助, 烦请点赞关注支持一波, 感激不尽
希望我的专栏能够帮助到你:
JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等
Java数据结构: 顺序表, 链表, 堆, 二叉树, 二叉搜索树, 哈希表等
JavaEE初阶: 多线程, 网络编程, TCP/IP协议, HTTP协议, Tomcat, Servlet, Linux, JVM等(正在持续更新)

本篇继续分享七大排序算法中的 归并排序 , 其余六个算法也有介绍噢
想看哪个点哪个 : 直接插入排序, 选择排序, 希尔排序, 堆排序, 冒泡排序, 快速排序

---

提示：是正在努力进步的小菜鸟一只，如有大佬发现文章欠佳之处欢迎评论区指点~ 废话不多说，直接发车~

一、排序相关概念

1, 什么是排序

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作

以 int 类型数据从小到大排序为例：
排序前：4，1，3，6，8，7，2，5
排序后：1，2，3，4，5，6，7，8

---

2, 什么是排序的稳定性

稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。

以 int 类型数据从小到大排序为例：
排序前：4，1，3a，6，8，7，2，3b，5（3a 在 3b 之前）
排序后：1，2，3a，3b，4，5，6，7，8（3a 还在 3b 之前，稳定）
排序后：1，2，3b，3a，4，5，6，7，8（3a 不在 3b 之前，不稳定）

3, 七大排序分类

以下是常见的 7大排序 算法

---

二、归并排序

1, 图文解析

归并排序 是建立在归并操作上的一种有效的排序算法, 该算法是采用分治法（Divide andConquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

基本思想：假如一个学校只有两个班，怎么算出全校成绩排名呢，一般是先在各自班里排好序，然后两个班再一起排序，在两个班的成绩表各自有序的情况下，合并起来排序肯定要比整体混乱着排序效率高
假如一个班1000个人，那在班内排名也是相对效率低的，那咋办？可以再把每个班分成若干个小组先排，再合并几个小组整体排序，这不就是递归吗

归并归并，我的理解就是，递归分割原始数组，分割到足够小时，递归结束，然后返回时合并，并且完成排序

过程图解：

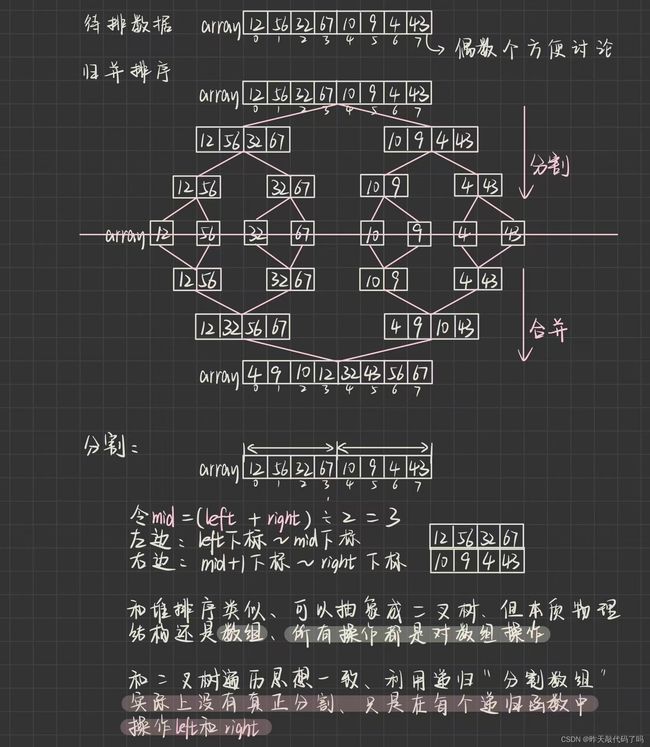
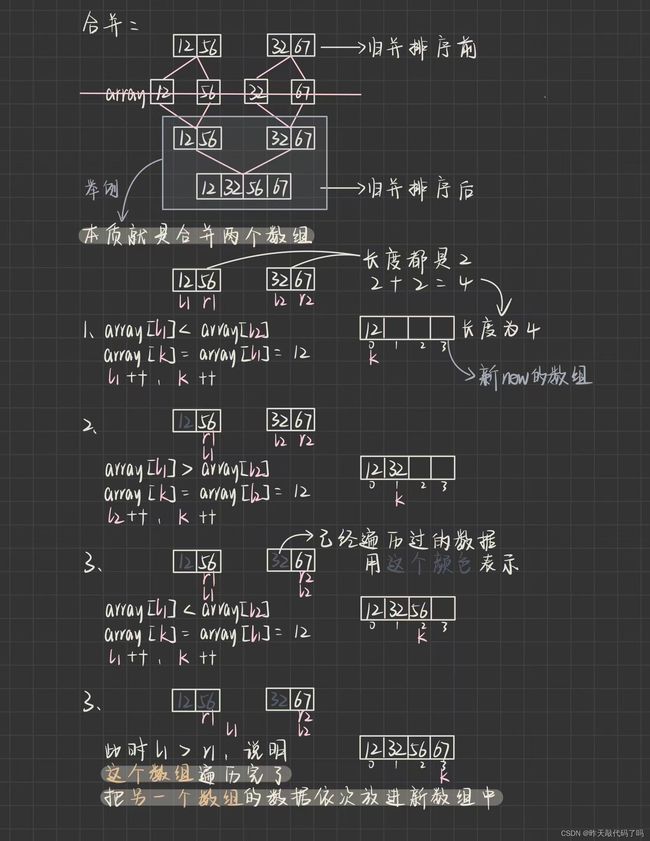
⚠️⚠️需要重点理解的是：
❗️❗️在递归进行分割的过程中，没有在物理上真正把数组切开（new了新的数组空间）的，只是函数的参数列表中有数组，left 和 right 下标，只是改变了 left 和 right 的值

❗️❗️但是在归并的过程中，才是真正的把两个数组的数据合起来（new了新的数组空间），然后再遍历挨个拷贝回原始数组中的。

---

2, 代码实现

体现封装的思想：把分割和合并两个方法独立封装起来，并设置成private

  /**
     * 归并排序
     * 时间复杂度：O（N^logN）
     * 空间复杂度：O（N）
     * 稳定性：稳定
     * @param array
     */
    public static void mergeSort(int[] array) {
        divid(array, 0, array.length - 1);
    }

    private static void divid(int[] array, int left, int right) {
        if (left >= right) {
            return;
        }
        int mid = (left + right) >>> 1;
        divid(array, left, mid);
        divid(array, mid + 1, right);
        merge(array, left, right, mid);
    }

    private static void merge(int[] array, int left, int right, int mid) {
        // 其实就是合并两个数组，并使合并后的数组有序
        int l1 = left;
        int l2 = mid + 1;
        int[] tmp = new int[right - left + 1];
        int i = 0;
        while(l1 <= mid && l2 <= right) {
            // 为什么要加等号，防止死循环
            if(array[l1] <= array[l2]) {
                tmp[i++] = array[l1++];
            }
            if (array[l2] <= array[l1]) {
                tmp[i++] = array[l2++];
            }
        }
        // 判断哪个数组还有数据
        while(l1 <= mid) {
            tmp[i++] = array[l1++];

        }
        while(l2 <= right) {
            tmp[i++] = array[l2++];
        }
        for (int j = 0; j < tmp.length; j++) {
            array[j + left] = tmp[j];
        }
    }

⚠️⚠️
注意最后一个 for 循环，这段代码作用是把合并好的有序子数组挨个拷贝回原始数组，但是 array[ j + left ] = tmp[j] 如何理解❓

因为你左右树都递归进行分割合并啊！如果原本在原始数组右边的子数组排有序之后, 应该从原数组的对应位置依次拷贝子数组

如果没有 j + left 这个操作, 就相当于每次都从原数组的 0 下标开始拷贝子数组

---

三、性能分析

时间复杂度：：
和快速排序类似，也是递归次数+每次的 i，j 遍历时间，最好最坏平均情况的时间复杂度都是O（N*log₂N）

空间复杂度：：
递归的开销是O（log₂N），但是需要总长度为N的额外数组空间的消耗，所有总体空间复杂度是O（N+log₂N）

稳定性：：
稳定

只要是交换时, 两数据相邻就是稳定的算法,只要是跳跃式的交换就是不稳定, 当然别忘了, 稳定的算法也可以修改代码更改成不稳定的

---

四、七大排序算法总体分析

建议对七大算法都有认识之后, 再对比分析~~
想看哪个点哪个 : 直接插入排序, 选择排序, 希尔排序, 堆排序, 冒泡排序, 快速排序

没有完美的排序算法,任何一种算法都是有优点和缺陷的,即便是大名鼎鼎的快速排序,也只是整体上效率比较高,性能相对更优越

现在就整体分析一下各种排序的优缺点

早期的排序算法平均时间复杂度都是O(N^2); 因为原理比较简单, 但性能较差, 所以 一般把直接插入排序,选择排序,冒泡排序归为简单排序一类, 另外四种排序都归于 改进排序

从平均情况看:
改进过的排序: 希尔排序, 堆排序, 归并排序, 快速排序要胜过简单排序的性能, 而四个改进算法中, 希尔排序的性能最差

时间复杂度:
直接插入排序和冒泡排序最快

从最好情况看从最坏情况看:
堆排序和归并排序的性能更胜过快排和其他简单排序

综合来看:
堆排序和归并排序比较稳定和强大, 情况最坏时好用
直接插入排序和冒泡排序, 最好情况时最好用,
而快速排序比较极端, 最好最坏情况都有缺陷 但是 快速排序能够称之为快速排序, 是因为它的综合性能最强，一般情况下是最快的

---

从稳定性来看:
改进排序中只有归并排序

从数据个数上看:
数据量越少, 越适合用简单排序, 因为堆排, 快速排序, 归并排序, 都用到了递归, 对于少量数据排序有点"炮弹打蚊子"

只要是交换时, 两数据相邻就是稳定的算法,只要是跳跃式的交换就是不稳定, 当然别忘了, 稳定的算法也可以修改代码更改成不稳定的

---

如果本篇对你有帮助，请点赞收藏支持一下，小手一抖就是对作者莫大的鼓励啦~

---

上山总比下山辛苦
下篇文章见