Day63｜图part2：广度优先搜索理论基础、200. 岛屿数量

广度优先搜索理论基础（BFS）

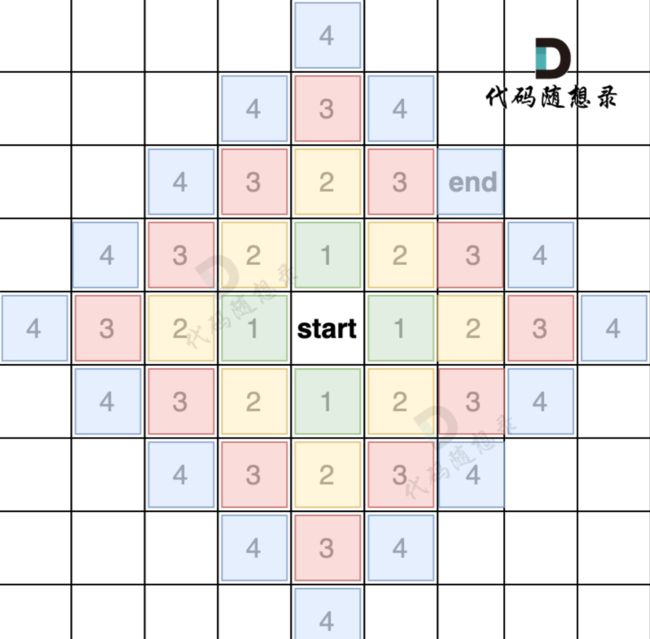
bfs适合解决什么类型的问题：广搜的搜索方式就适合于解决两个点之间的最短路径问题。BFS 找到的路径一定是最短的，但代价就是空间复杂度可能比 DFS 大很多

当然，也有一些问题是广搜 和 深搜都可以解决的，例如岛屿问题，这类问题的特征就是不涉及具体的遍历方式，只要能把相邻且相同属性的节点标记上就行。

示意图：

用什么数据结构？一般使用队列。

很多网上的资料都是直接说用队列来实现。

其实，我们仅仅需要一个容器，能保存我们要遍历过的元素就可以，那么用队列，还是用栈，甚至用数组，都是可以的。

用队列的话，就是保证每一圈都是一个方向去转，例如统一顺时针或者逆时针。

因为队列是先进先出，加入元素和弹出元素的顺序是没有改变的。

如果用栈的话，就是第一圈顺时针遍历，第二圈逆时针遍历，第三圈有顺时针遍历。

为了简便和之前知识做衔接，还是使用队列。

BFS框架

int BFS(Node start, Node target) {
    queue<Node> q; 
    set<Node> visited;
    
    q.push(start); 
    visited.insert(start);

    while (!q.empty()) {
        int sz = q.size();
        for (int i = 0; i < sz; i++) {
            Node cur = q.front();
            q.pop();
            if (cur == target)
                return step;
            for (Node x : cur.adj()) {
                if (visited.count(x) == 0) {
                    q.push(x);
                    visited.insert(x);
                }
            }
        }
    }
    // 如果走到这里，说明在图中没有找到目标节点
}

cur.adj() 泛指 cur 相邻的节点，比如说二维数组中，cur 上下左右四面的位置就是相邻节点；visited 的主要作用是防止走回头路，大部分时候都是必须的，但是像一般的二叉树结构，没有子节点到父节点的指针，不会走回头路就不需要 visited。

200. 岛屿数量

leetcode链接：题目链接

给你一个由 '1'（陆地）和 '0'（水）组成的的二维网格，请你计算网格中岛屿的数量。

岛屿总是被水包围，并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。

此外，你可以假设该网格的四条边均被水包围。

示例 1：

输入：grid = [
  ["1","1","1","1","0"],
  ["1","1","0","1","0"],
  ["1","1","0","0","0"],
  ["0","0","0","0","0"]
]
输出：1
示例 2：

输入：grid = [
  ["1","1","0","0","0"],
  ["1","1","0","0","0"],
  ["0","0","1","0","0"],
  ["0","0","0","1","1"]
]
输出：3

岛屿问题面试常考，就是靠BFS或DFS遍历二维数组。

本题思路，是用遇到一个没有遍历过的节点陆地，计数器就加一，然后把该节点陆地所能遍历到的陆地都标记上。（也就是把起相邻的都标记成一个）

在遇到标记过的陆地节点和海洋节点的时候直接跳过。 这样计数器就是最终岛屿的数量。

DFS解法

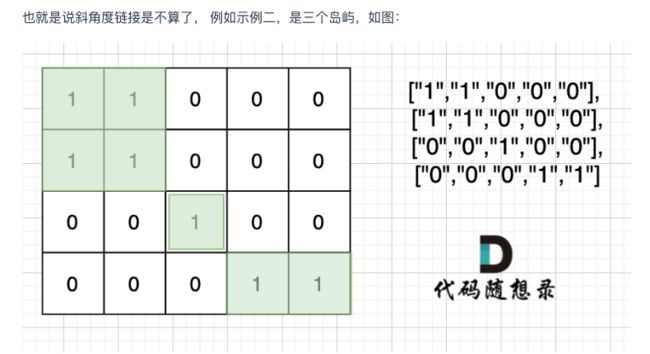
求岛屿数量，就是求多少个1是相连的，这里注意对角线相连不算：

我们首先来看下使用DFS遍历二维数组的代码框架：

void dfs(vector<vector<int>>& grid, int i, int j, vector<vector<bool>>& visited) {
    int m = grid.size(), n = grid[0].size();
    if (i < 0 || j < 0 || i >= m || j >= n) {
        return;
    }
    if (visited[i][j]) {
        return;
    }
    visited[i][j] = true;
    dfs(grid, i - 1, j, visited); // 上
    dfs(grid, i + 1, j, visited); // 下
    dfs(grid, i, j - 1, visited); // 左
    dfs(grid, i, j + 1, visited); // 右
}

下面的四行代码复用性很强其实可以省略，解决的方法就是使用方向数组：

vector<vector<int>> dirs = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
...
...
...
for (auto &d : dirs) {
        int next_i = i + d[0];
        int next_j = j + d[1];
        dfs(grid, next_i, next_j, visited);
    }

这两种写法是一样的，但后者更简洁。比如后面有8个方向呢？没必要把八个方向都写一遍。

因此稍作修改可提出本题的dfs代码：

void dfs(vector<vector<char>> &grid, int i, int j ){
        if (i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size()) {
            // 超出索引边界
            return;
        }
        if (grid[i][j] == '0') {
            // 已经是海水了
            return;
        }
        // 将 (i, j) 变成海水
        grid[i][j] = '0';
        // 淹没上下左右的陆地
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);

    }

这里的grid[i][j]起到了类似visited数组的作用。那么如何标记岛屿？

• 每遍历一个岛屿，岛屿数量+1
• 然后用dfs把岛屿淹了，就是化成0，这是相邻的岛屿块都会被淹
• 最后都被淹了就返回最终岛屿数量。(因为不相邻的岛屿块没办法淹）

    int numIslands(vector<vector<char>>& grid) {
        int res = 0;
        for(int i = 0; i < grid.size(); i++){
            for(int j = 0; j < grid[0].size(); j++){
                if(grid[i][j] == '1'){
                    res++;
                }
                dfs(grid, i , j);
            }
        }
        return res;
    }
};

最终代码：

class Solution {
public:
    void dfs(vector<vector<char>> &grid, int i, int j ){
        if (i < 0 || j < 0 || i >= grid.size() || j >= grid[0].size()) {
            // 超出索引边界
            return;
        }
        if (grid[i][j] == '0') {
            // 已经是海水了
            return;
        }
        // 将 (i, j) 变成海水
        grid[i][j] = '0';
        // 淹没上下左右的陆地
        dfs(grid, i + 1, j);
        dfs(grid, i, j + 1);
        dfs(grid, i - 1, j);
        dfs(grid, i, j - 1);

    }
    int numIslands(vector<vector<char>>& grid) {
        int res = 0;
        for(int i = 0; i < grid.size(); i++){
            for(int j = 0; j < grid[0].size(); j++){
                if(grid[i][j] == '1'){
                    res++;
                    dfs(grid, i , j);
                }
                
            }
        }
        return res;
    }
};

为什么每次遇到岛屿，都要用 DFS 算法把岛屿「淹了」呢？主要是为了省事，避免维护 visited 数组。

因为 dfs 函数遍历到值为 0 的位置会直接返回，所以只要把经过的位置都设置为 0，就可以起到不走回头路的作用。

这类 DFS 算法还有个别名叫做 FloodFill 算法，还是很贴切的。

BFS解法

不少同学用广搜做这道题目的时候，超时了。 这里有一个广搜中很重要的细节：

根本原因是只要 加入队列就代表 走过，就需要标记，而不是从队列拿出来的时候再去标记走过。

最终代码：

private:
int dir[4][2] = {0, 1, 1, 0, -1, 0, 0, -1}; // 四个方向
void bfs(vector<vector<char>>& grid, vector<vector<bool>>& visited, int x, int y) {
    queue<pair<int, int>> que;
    que.push({x, y});
    visited[x][y] = true; // 只要加入队列，立刻标记
    while(!que.empty()) {
        pair<int ,int> cur = que.front(); que.pop();
        int curx = cur.first;
        int cury = cur.second;
        for (int i = 0; i < 4; i++) {
            int nextx = curx + dir[i][0];
            int nexty = cury + dir[i][1];
            if (nextx < 0 || nextx >= grid.size() || nexty < 0 || nexty >= grid[0].size()) continue;  // 越界了，直接跳过
            if (!visited[nextx][nexty] && grid[nextx][nexty] == '1') {
                que.push({nextx, nexty});
                visited[nextx][nexty] = true; // 只要加入队列立刻标记
            }
        }
    }
}
public:
    int numIslands(vector<vector<char>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<bool>> visited = vector<vector<bool>>(n, vector<bool>(m, false));

        int result = 0;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                if (!visited[i][j] && grid[i][j] == '1') {
                    result++; // 遇到没访问过的陆地，+1
                    bfs(grid, visited, i, j); // 将与其链接的陆地都标记上 true
                }
            }
        }
        return result;
    }

总结

• DFS适合找全部路径，BFS适合找最短路径；
• DFS需要递归，BFS不需要递归；
• FloodFill算法