mysql无限分类表结构_MySql无限分类结构

无限分类是我们开发中非常普遍的应用，例如论坛，CMS类别，并且应用特别多.

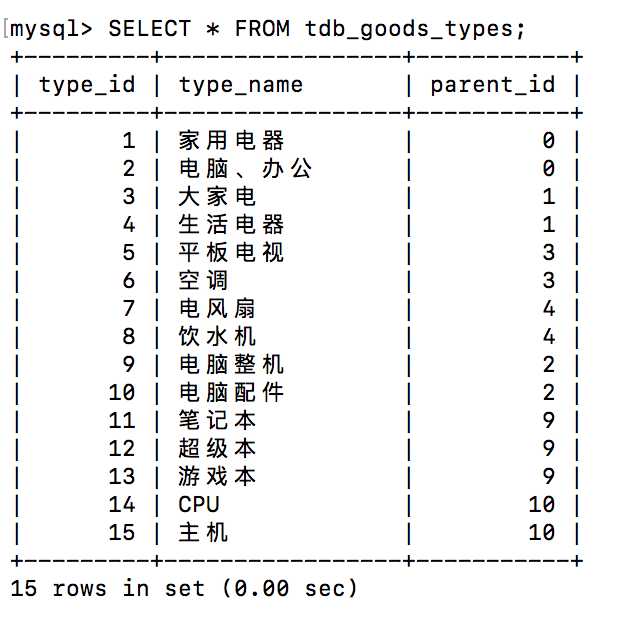
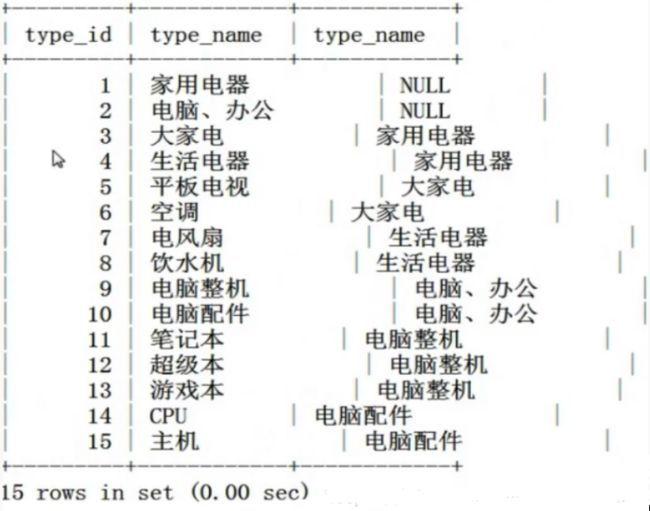
我们最常用和最简单的方法是MySql中的ID，parentID，名称:

优点是结构简单.

缺点是效率不高，因为每次递归都必须查询，并且在有数百个的情况下不是很快！

存储树是一个常见问题，有多种解决方案. 主要有两种方法: 建立邻接表模型和修改树序遍历算法.

我们将讨论这两种方法的节能水平数据. 我将以一个假想的食品商店中的树为例. 这家食品店按颜色和类型组织其食品类别. 这棵树看起来像这样:

接下来，我们将使用另一种方法，即修改后的订单树遍历算法(modifiedpreordertreetraversalalgorithm).

您可能较少接触这种方法，并且第一次使用上面的方法并不容易理解，但是由于该方法不使用递归查询算法，因此查询效率更高.

我们首先按照以下方式在纸上绘制多级数据，在根节点Food的左侧写1，然后继续沿着树，在Fruit的左侧写2，然后继续沿着整个树的边缘在每个节点的左侧和右侧标记数字. 在食物的右边，最后一个数字是18. 在下面的图片中，您可以看到标记的整数的多层结构. (不明白吗？请用手指将数字从1指向18，以了解发生了什么. 如果不明白，请再次数数并注意移动手指. )

这些数字表示各个节点之间的关系. “红色”的数字是3和6，它们是“食物” 1-18的后代. 同样，我们可以看到所有左值大于2且右值小于11的节点都是“水果” 2-11的后代

如图所示:

通过这种方式mysql 无限分类，让我们看一下下面编译的数据表.

注意: 由于“ left”和“ right”在SQL中具有特殊含义，因此我们需要使用“ lft”和“ rgt”表示左字段和右字段. 另外，在此结构中，不再需要“父”字段来表示树结构. 换句话说，下面的表结构就足够了.

选择*从2和11之间的树中查找；

看，您只需一个查询即可获得所有这些节点. 为了像上面的递归函数一样显示整个树结构，我们还需要对此类查询进行排序. 按节点的左值排序:

从*在2和11之间按lft ASC排序的树中选择*.

那么一个节点有多少个后代节点？很简单，后代总数=(右值-左值-1)/ 2

descendants =(right–left-1)/ 2，如果您不太清楚此公式，请转到下一本书，我们在上面的数据结构中清楚地写了它！

在同一级别添加节点的方法如下:

LOCK TABLE nested_category WRITE;

SELECT @myRight: = rgt from nested_category

WHERE name ='Cherry';

UPDATE nested_category SET rgt = rgt + 2 WHERE rgt> @myRight;

UPDATE nested_category SET lft = lft + 2 WHERE lft> @myRight;

INSERT INTO nested_category(name，lft，rgt)VALUES('Strawberry'，@myRight + 1，@myRight + 2);

解锁表；

添加树的子节点的方法如下:

LOCK TABLE nested_category WRITE;

SELECT @myLeft: =从nested_category中查找

WHERE name ='Beef';

UPDATE nested_category SET rgt = rgt + 2 WHERE rgt> @myLeft;

UPDATE nested_category SET lft = lft + 2 WHERE lft> @myLeft;

INSERT INTO nested_category(name，lft，rgt)VALUES('charqui'，@myLeft + 1，@myLeft + 2);

解锁表；

插入节点后，可以使用以下SQL查看和验证:

SELECT CONCAT(REPEAT(‘’，(COUNT(parent.name)– 1))，node.name)AS名称

FROM nested_category AS节点，

nested_category AS父级

在parent.lft和parent.rgt之间的node.lft

GROUP BY node.name

ORDER BY node.lft;

删除节点的方法有点麻烦，因为存在一个中间变量，如下所示:

LOCK TABLE nested_category WRITE;

选择@myLeft: = lft，@myRight: = rgt，@myWidth: = rgt – lft + 1

FROM nested_category

WHERE name ='Cherry';

从nested_category中删除@myLeft和@myRight之间的位置；

UPDATE nested_category SET rgt = rgt – @myWidth WHERE rgt> @myRight;

UPDATE nested_category SET lft = lft – @myWidth WHERE lft> @myRight;

解锁表；

这种方法有点难以理解，但适用于使用数据. 只需两个SQL语句即可查看所有结构. 添加和删​​除节点时比较麻烦，但是与之相比，仍然值得这样做. 这个发现使我发现结构确实有用，但是我基本上忘记了我在学校学到的树. 这次我在将其应用到项目之前遇到了这个问题！

参考文章:

本文来自电脑杂谈，转载请注明本文网址：

http://www.pc-fly.com/a/jisuanjixue/article-276166-1.html