《DATASET DISTILLATION》
这篇文章提出了数据浓缩的办法,在前面已有的知识浓缩(压缩模型)的经验上,提出了不压缩模型,转而压缩数据集的办法,在压缩数据集上训练模型得到的效果尽可能地接近原始数据集的效果。
摘要
模型蒸馏的目的是将复杂模型的知识提炼为简单模型的知识。在本文中考虑了一个替代的公式,称为数据集蒸馏:我们保持模型固定,而不是尝试从一个大的训练数据集提取知识到一个小的。其思想是合成少量的数据点,这些数据点不需要来自于正确的数据分布,但当给学习算法作为训练数据时,会近似于在原始数据上训练的模型。例如,文章展示了可以将6万幅MNIST训练图像压缩成10幅合成蒸馏图像(每类一张),在给定一个固定的网络初始化条件下,只需几个梯度下降步骤,就可以达到接近原始性能的效果。
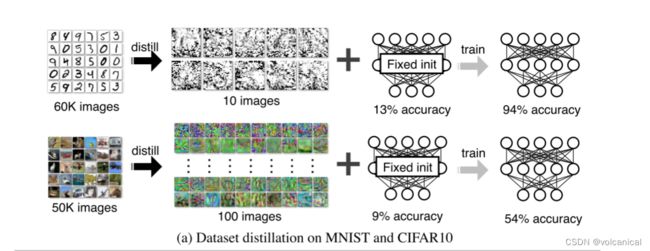
效果1:使用压缩后的图片进行训练,10张MNIST或者100张CIFAR10,就可以达到94%的准确率和54%的准确率。
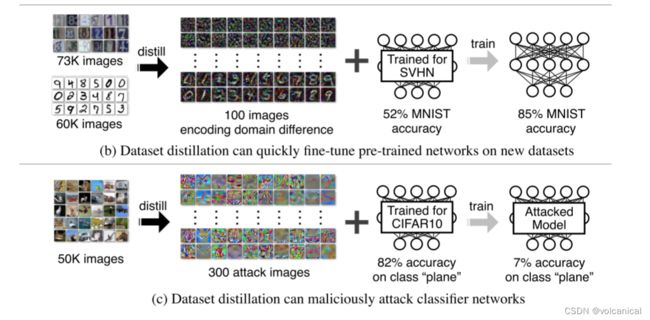
效果2:使用压缩数据进行fine-tune,可以很好地微调数据集效果。
效果3:将攻击数据集浓缩,可以更好地强化攻击的效果,仅仅用300张图片就使得目标类的分类准确率降低至7%。
相关工作:
Pass
方法:
准备工作
考虑有数据集 x = { x i } i = 1 N \mathbf{x}=\left\{x_i\right\}_{i=1}^N x={xi}i=1N为原始数据集,神经网络为 θ \theta θ, ℓ ( x i , θ ) \ell\left(x_i, \theta\right) ℓ(xi,θ)是 x i x_i xi在模型 θ \theta θ上的损失。
θ ∗ = arg min θ 1 N ∑ i = 1 N ℓ ( x i , θ ) ≜ arg min θ ℓ ( x , θ ) \theta^*=\underset{\theta}{\arg \min } \frac{1}{N} \sum_{i=1}^N \ell\left(x_i, \theta\right) \triangleq \underset{\theta}{\arg \min } \ell(\mathbf{x}, \theta) θ∗=θargminN1i=1∑Nℓ(xi,θ)≜θargminℓ(x,θ)
上式就是神经网络优化的最终目标,训练获得一个 θ ∗ \theta^* θ∗使得模型在数据集上的损失最小。
这里为了方便,直接将
ℓ ( x , θ ) \ell(\mathbf{x}, \theta) ℓ(x,θ)
记为数据集上的损失平均和
优化浓缩数据
浓缩数据和浓缩学习率都是随机初始化的,通过不断地计算损失梯度下降,优化得到最终的浓缩数据集以及浓缩学习率,如何获得优化函数便是这里的重点。
x ~ = { x ~ i } i = 1 M \tilde{\mathbf{x}}=\left\{\tilde{x}_i\right\}_{i=1}^M x~={x~i}i=1M中 M ≪ N M \ll N M≪N 并且对应的学习率 η ~ \tilde{\eta} η~,对应的梯度下降为:
θ 1 = θ 0 − η ~ ∇ θ 0 ℓ ( x ~ , θ 0 ) \theta_1=\theta_0-\tilde{\eta} \nabla_{\theta_0} \ell\left(\tilde{\mathbf{x}}, \theta_0\right) θ1=θ0−η~∇θ0ℓ(x~,θ0)
使用生成的浓缩数据集 x ~ \tilde{\mathbf{x}} x~ 可以极大地增强训练的效果。给定一个初始的 θ 0 \theta_0 θ0,我们获得 x ~ \tilde{\mathbf{x}} x~ 和学习率 η ~ \tilde{\eta} η~ 通过最小化以下损失函数 L \mathcal{L} L :
x ~ ∗ , η ~ ∗ = arg min x ~ , η ~ L ( x ~ , η ~ ; θ 0 ) = arg min x ~ , η ~ ℓ ( x , θ 1 ) = arg min x ~ , η ~ ℓ ( x , θ 0 − η ~ ∇ θ 0 ℓ ( x ~ , θ 0 ) ) , \tilde{\mathbf{x}}^*, \tilde{\eta}^*=\underset{\tilde{\mathbf{x}}, \tilde{\eta}}{\arg \min } \mathcal{L}\left(\tilde{\mathbf{x}}, \tilde{\eta} ; \theta_0\right)=\underset{\tilde{\mathbf{x}}, \tilde{\eta}}{\arg \min } \ell\left(\mathbf{x}, \theta_1\right)=\underset{\tilde{\mathbf{x}}, \tilde{\eta}}{\arg \min } \ell\left(\mathbf{x}, \theta_0-\tilde{\eta} \nabla_{\theta_0} \ell\left(\tilde{\mathbf{x}}, \theta_0\right)\right), x~∗,η~∗=x~,η~argminL(x~,η~;θ0)=x~,η~argminℓ(x,θ1)=x~,η~argminℓ(x,θ0−η~∇θ0ℓ(x~,θ0)),
现在看着可能会很抽象,这里简单的讲解一下,方法就是:
- 先使用随机初始化的 x ~ \tilde{\mathbf{x}} x~和 η ~ \tilde{\eta} η~,将浓缩数据集 x ~ \tilde{\mathbf{x}} x~和浓缩学习率 η ~ \tilde{\eta} η~丢入神经网络 θ 0 \theta_0 θ0进行一轮训练。
- 使用原始数据集 检验 使用浓缩数据集 x ~ \tilde{\mathbf{x}} x~和浓缩学习率 η ~ \tilde{\eta} η~训练得到的新一轮神经网络 θ 1 \theta_1 θ1,计算原始数据集在这个模型上的损失。
- 这个损失就是我们的优化目标,我们要让这个损失最小。
模型随机初始化
上面的函数中,模型总是使用 θ 0 \theta_0 θ0进行训练获得浓缩数据集和浓缩学习率,作者担心这样获得的浓缩数据集和浓缩学习率会和 θ 0 \theta_0 θ0有较大的关系,不能很好地泛化到其他初始化,因此作者又提出使用随机的 θ 0 \theta_0 θ0来训练。
于是作者就改成,每一轮的 θ \theta θ都不同, θ 0 \theta_0 θ0是一个满足 p ( θ ) p(\theta) p(θ)的分布。
SGD下降法
每次选中一个batch,每个batch使用不同的初始化,就是把之前的GD修改为minibatch梯度下降。
具体算法如下图所示:
将原始数据集划分为 x t x_t xt的batch,每一个batch有不同的初始化 θ 0 \theta_0 θ0,每一个batch的计算方法与前面相同,最后将每个batch计算获得的 x ~ \tilde{\mathbf{x}} x~和 η ~ \tilde{\eta} η~平均。