栈与队列经典题目——用队列实现栈

本篇文章讲解栈和队列这一部分知识点的经典题目：用栈实现队列、用队列实现栈。对应的题号分别为：Leetcode.225——用队列实现栈，。

在对两个题目进行解释之前，先回顾以下栈和队列的特点与不同：

栈是一种特殊的线性表，并且只能在尾部进行插入、删除的操作。对于栈的实现，可以通过顺序表或者链表的思路来达成。但是，参考栈只能在尾部进行插入、删除操作的特点。一般采用顺序表进行实现。

队列也是一种特殊的线性表，只能在队尾进行插入操作，在队头进行删除操作。鉴于队列的这一性质，一般采用链表来实现队列。

1.Leetcode.225——用队列实现栈：

题目如下：

1.1 思路分析：

给出下列一个栈：

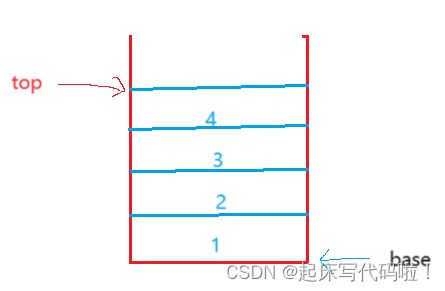
在栈中，遵从后进先出的原则。但是，本题要求是利用队列来实现栈。对于队列来说，出数据只能从队头进行。题目中要求利用两个队列来实现栈的功能，对于本功能，思路如下：
给定下面两个队列，分别命名为,

按照题目中的要求，需要移除元素。对于队列来说，移除元素只能从队头进行。所以，先把中的元素都移动到中。此时效果如下：

此时，再对进行一次取队头元素的操作即可。 下面为了方便表达，将简称为,简称为

由上述分析可知。解决本题的关键就是在使用两个队列时，需要让一个队列中存储元素，另一个队列保持为空。当需要进行返回栈顶元素的操作时，再让为空的队列保存另一个队列中的前项元素。所以，一个队列用于存储元素，一个用于保持空状态为了方便表达。下面，会默认创建两个结构体指针：，来存储的地址，来存储的地址。并在后续会针对二者谁为空进行判断。

（注：下面只给出各种给定功能的实现方法，在进行解题时，需要预先将编写好的xiami码复制到题目上方，本文采用一起学数据结构（6）——栈和队列_起床写代码啦！的博客-CSDN博客

中的队列） 

1.2 各功能的实现：

 1.2.1 栈的创建及初始化：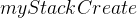

前面说到，需要一个用于存储元素的队列，一个保持空状态的队列。但是对于二者谁为空，在后续的操作中进行判断即可。在本功能中不需要进行判断。代码如下：

//创建队列
typedef struct {
    Que q1;
    Que q2;
} MyStack;

//初始化队列，注意，返回值返回地址，需要采用malloc返回以保证返回时不会因为变量的局部性成为野指针
MyStack* myStackCreate() {
    MyStack* obj = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&obj->q1);
    QueueInit(&obj->q2);

    return obj;
}

1.2.2 向栈中插入元素myStackPush：

为了保证为空，不为空，所以，在向栈中插入元素时，需要向中插入。在初始化这一步骤中，并没有分辨哪个队列为空，在本步骤并不需要明确知道哪个队列为空，只需要利用函数判断队列是否为空，如果为空，此时为，直接向中进行插入，反之则向中插入，代码如下：

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

1.2.3 移除并返回栈顶元素 myStackPop：

在思路分析中，已经给出了该功能的实现方法。即，让指向的队列中的前项元素移动到所对应的元素。在移动元素之前，需要先判断哪个队列为空。方法如下：

首先创建结构体指针，。让二者分别指向队列。利用函数判断此时的是否为空，若为空，则不做改变。若不为空，则令，中存储的地址交换。

代码如下：

int myStackPop(MyStack* obj) {
    Que* noempty = &obj->q1;
    Que* empty = &obj->q2;
    if(!QueueEmpty(empty))
    {
        noempty = &obj->q2;
        empty = &obj->q1;
    } 

}

再判断出哪个队列为，哪个队列为后，进行下一步。首先，利用函数取出中的队头元素，再利用函数将取出的元素插入到中。

题目要求，移除并且返回。所以需要额外创建一个变量用于存储栈顶元素。之后再利用函数移除栈顶元素，最后返回即可。代码如下：
 

int myStackPop(MyStack* obj) {
    Que* noempty = &obj->q1;
    Que* empty = &obj->q2;
    if(!QueueEmpty(empty))
    {
        noempty = &obj->q2;
        empty = &obj->q1;
    }
    while( QueueSize(noempty) > 1)
    {
        QueuePush(empty,QueueFront(noempty));
        QueuePop(noempty);
    }
    int Top = QueueFront(noempty);
    QueuePop(noempty);

    return Top;
    

}

1.2.4 返回栈顶元素myStackTop：

栈顶元素所对应的位置就是队列的队尾。所以，只需要采用向栈中插入元素的方法，通过函数，对不满足的队列（即非空队列）调用函数，返回函数的返回值即可。代码如下：

int myStackTop(MyStack* obj) {
  if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

1.2.5 探空myStackEmpty：

原理较为简单，只给出代码：

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
  
}

1.2.6 释放动态开辟的空间myStackFree：
代码如下：

void myStackFree(MyStack* obj) {
    QueueDestory(&obj->q1);
    QueueDestory(&obj->q2);

    free(obj);
}

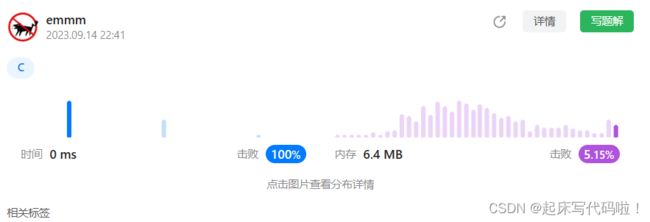
2.结果展示及题解代码总览：

2.1 结果展示：

 

2.2 题解代码总览：

typedef int QDataType;
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;


typedef struct Queue
{
	QNode* phead;
	QNode* tail;
	int size;
}Que;


//初始化
void QueueInit(Que* ps);
//销毁
void QueueDestory(Que* ps);
//插入元素
void QueuePush(Que* ps, QDataType x);
//删除元素
void QueuePop(Que* ps);
//取头部元素
QDataType QueueFront(Que* ps);
//取尾部元素
QDataType QueueBack(Que* ps);
//探空
bool QueueEmpty(Que* ps);
//求长度
int QueueSize(Que* ps);


void QueueInit(Que* ps)
{
	assert(ps);
	ps->phead = ps->tail = 0;
	ps->size = 0;
}

void QueuePush(Que* ps, QDataType x)
{
	assert(ps);

	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	if (newnode == NULL)
	{
		perror("malloc");
		exit(-1);
	}

	newnode->next = NULL;
	newnode->data = x;

	if (ps->tail == NULL)
	{
		ps->phead = ps->tail = newnode;
	}
	else
	{
		ps->tail->next = newnode;
		ps->tail = newnode;
	}
	ps->size++;
}

void QueuePop(Que* ps)
{
	assert(ps);
	assert(!QueueEmpty(ps));
	if (ps->phead->next == NULL)
	{
		free(ps->phead);
		ps->phead = ps->tail = NULL;
	}
	else
	{
		QNode* next = ps->phead->next;
		free(ps->phead);
		ps->phead = next;
	}
	ps->size--;
}

QDataType QueueFront(Que* ps)
{
	assert(ps);
	assert(!QueueEmpty(ps));

	return ps->phead->data;
}

QDataType QueueBack(Que* ps)
{
	assert(ps);
	assert(!QueueEmpty(ps));

	return ps->tail->data;
}

bool QueueEmpty(Que* ps)
{
	assert(ps);

	return ps->phead == NULL;
}

int QueueSize(Que* ps)
{
	assert(ps);


	return ps->size;
}

void QueueDestory(Que* ps)
{
	assert(ps);

	QNode* cur = ps->phead;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	ps->phead = ps->tail = NULL;
	ps->size = 0;
}

//创建队列
typedef struct {
    Que q1;
    Que q2;
} MyStack;

//初始化队列，注意，返回值返回地址，需要采用malloc返回以保证返回时不会因为变量的局部性成为野指针
MyStack* myStackCreate() {
    MyStack* obj = (MyStack*)malloc(sizeof(MyStack));
    QueueInit(&obj->q1);
    QueueInit(&obj->q2);

    return obj;
}

void myStackPush(MyStack* obj, int x) {
    if(!QueueEmpty(&obj->q1))
    {
        QueuePush(&obj->q1,x);
    }
    else
    {
        QueuePush(&obj->q2,x);
    }
}

//思路：将非空队列中前N-1项元素移到空队列中
int myStackPop(MyStack* obj) {
    Que* noempty = &obj->q1;
    Que* empty = &obj->q2;
    if(!QueueEmpty(empty))
    {
        noempty = &obj->q2;
        empty = &obj->q1;
    }
    while( QueueSize(noempty) > 1)
    {
        QueuePush(empty,QueueFront(noempty));
        QueuePop(noempty);
    }
    int Top = QueueFront(noempty);
    QueuePop(noempty);

    return Top;
    

}

int myStackTop(MyStack* obj) {
  if(!QueueEmpty(&obj->q1))
    {
        return QueueBack(&obj->q1);
    }
    else
    {
        return QueueBack(&obj->q2);
    }
}

bool myStackEmpty(MyStack* obj) {
    return QueueEmpty(&obj->q1) && QueueEmpty(&obj->q2);
  
}

void myStackFree(MyStack* obj) {
    QueueDestory(&obj->q1);
    QueueDestory(&obj->q2);

    free(obj);
}