TopK问题详解

TopK问题

注：本篇对于TopK问题的讲解建立在数据结构——堆的基础之上，如果对堆还不太了解的朋友，建议先看看数据结构——堆

1. 什么是TopK问题

Top-K问题是一类算法和数据处理问题，其中任务是从一个包含大量数据项的集合中找到前K个最重要或最高排名的元素。这个问题在计算机科学和数据处理领域中广泛存在，有多种不同的应用场景，例如：

1. 搜索引擎：在搜索引擎中，Top-K问题可以用于返回用户查询的前K个最相关的搜索结果。
2. 推荐系统：在电子商务网站或媒体流推荐中，可以使用Top-K问题来提供用户最感兴趣的产品或内容。
3. 数据分析：在大数据分析中，Top-K问题可用于查找最频繁出现的元素或最高价值的数据点。
4. 数据挖掘：在聚类和分类问题中，可以使用Top-K问题来选择具有最高重要性的特征或数据点。

解决Top-K问题的算法可以根据具体的情况而异，通常包括排序、堆排序、快速选择等技术，目的是高效地找到前K个元素，而不必处理整个数据集。这些算法在处理大规模数据时非常有用，因为它们可以减少计算时间和内存需求。

---

2. 怎么用堆来处理TopK问题

2.1 引例

先来看一个引例：从数据个数为15的数组nums中找到前k = 5个最大的数

最直观的做法，就是建立一个大堆，然后用HeapPop的方法删除k次数据，就可以得到前k个最大的数据了。

示例代码：

void PrintTopK(int* nums, int numsSize, int k)
{
	//先建大堆
	for (int i = (numsSize - 2) / 2; i >= 0; i--)
		AdjustDown(nums, numsSize, i);

	//找前k大的数据
    while (k--)
	{
		printf("%d ", nums[0]);	//堆顶数据就是当前最大值
		
        //删除堆顶数据
		Swap(&nums[0], &nums[numsSize - 1]);
		numsSize--;
		//向下调整，得到次大值
		AdjustDown(nums, numsSize, 0);
	}
}

这种做法看似没问题，但是当面对数千万乃至上亿的数据时，由于内存无法存储这么多数据，那我们也就不可能一次性建立这么大的堆，上面提到的方法也就不适用了。

2.2 TopK步骤及分析

下面才是TopK问题的正确做法（以找到前k个最大的数据为例）：

• 首先，将待查找的数据都存入到文件中
• 利用文件的读写操作，将文件的前k个数据建成小堆
• 逐个读取文件中的数据，如果该数据大于堆顶元素，那就替换堆顶元素进入堆中，并调整堆，确保堆结构的正确性
• 直到读取完整个文件，最后构成堆的k个元素，就是前k个最大的数据

有小伙伴可能会疑惑，为什么找前k个最大的数据要建小堆而不是大堆，

我们以数组nums = {2,4,1,5,3,6,7,8,9,10}, k = 5进行分析：

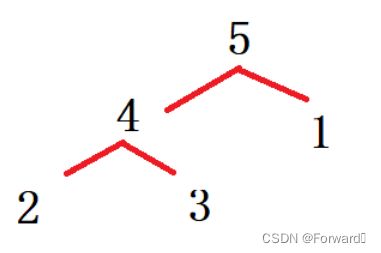
• 如果建大堆，那么堆的形状如下图所示：
• 此时我们只能保证堆顶数据是这k个数据的最大值，如果我们按上述操作对堆顶元素进行替换，那么也只能不断更新这个最大值，当读取完整个文件的数据后，我们也只能都到这所有数据的最大值（即堆顶元素），而无法得到前k个最大值

• 如果建小堆，那么堆的形状如图所示：
• 此时，我们可以保证堆顶数据是这k个数据的最小值，当遍历文件元素得到一个更大的值并进行替换后，这k个数据就会被更新，同时向下调整之后次小的的数就会变成堆顶，因此经过不断的替换，读取完文件后，组成堆的k个数据就是前k个最大数据

​ 具体过程如下：

3. TopK模拟实现

#include 
#include 
#include 
#include 

void Swap(int* num1, int* num2)
{
	int temp = *num1;
	*num1 = *num2;
	*num2 = temp;
}

//向下调整
void AdjustDown(int* nums, int numsSize, int parent)
{
	int child = parent * 2 + 1;

	while (child < numsSize)
	{
		if (nums[child] > nums[child + 1])
			child = child + 1;

		if (nums[parent] > nums[child])
		{
			Swap(&nums[parent], &nums[child]);

			parent = child;
			child = parent * 2 + 1;
		}
		else
			break;
	}
}

void NumsPrint(int* nums, int numsSize)
{
	for (int i = 0; i < numsSize; i++)
		printf("%d ", nums[i]);

	printf("\n");
}

//向文本中导入数据
void CreateNDate()
{
	// 造数据
	int n = 10000;
	srand((unsigned int)time(NULL));

	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (int i = 0; i < n; ++i)
	{
		int x = rand() % 1000000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

void PrintTopK(int k)
{
	//只读方式打开文件
	const char* file = "data.txt";
	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}

	//创建k大小的堆，并先存入k个数据
	int* minHeap = (int*)malloc(sizeof(int) * k);
	for (int i = 0; i < k; i++)
		fscanf(fout, "%d", &minHeap[i]);

	//建小堆
	for (int i = (k - 2) / 2; i >= 0; i--)
	{
		AdjustDown(minHeap, k, i);
	}

	//开始找TopK
	int temp;
	while (fscanf(fout, "%d", &temp) != EOF)
	{
		if (temp > minHeap[0])
		{
			minHeap[0] = temp;

			AdjustDown(minHeap, k, 0);
		}
	}

	NumsPrint(minHeap, k);

	fclose(fout);
	free(minHeap);
}

int main()
{
	CreateNDate();
    
    //调用PrintTopK函前，应该先用CreatNData函数像文本中导入数据
    //当需要调用PrintTopK函数时，CreatNData函数应该被注释掉，否则难以检测PrintTopK函数的正确性
	PrintTopK(5);

	return 0;
}