【力扣周赛】第 113 场双周赛（贪心&异或性质&换根DP）

竞赛链接

https://leetcode.cn/contest/biweekly-contest-113/

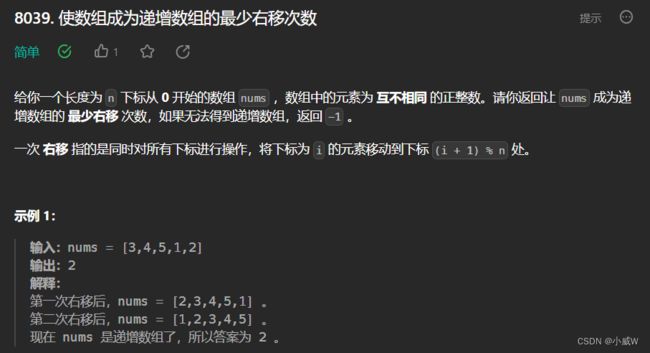
Q1：8039. 使数组成为递增数组的最少右移次数

https://leetcode.cn/problems/minimum-right-shifts-to-sort-the-array/

提示：

1 <= nums.length <= 100
1 <= nums[i] <= 100
nums 中的整数互不相同。

竞赛时代码——枚举答案

因为数据范围很小，所以可以从小到大枚举可能的答案。

class Solution {
    public int minimumRightShifts(List<Integer> nums) {
        int n = nums.size();
        // a 是排好序之后的数组，作为标准答案
        int[] a = new int[n];
        for (int i = 0; i < n; ++i) a[i] = nums.get(i);
        Arrays.sort(a);
        // 枚举答案，即枚举右移次数
        for (int x = 0; x < n; ++x) {
            boolean f = true;
            // 检查这个答案下每一位是否移动后相等
            for (int i = 0; i < n; ++i) {
                if (nums.get(i) != a[(i + x) % n]) {
                    f = false;
                    break;
                }
            }
            if (f) return x;
        }
        return -1;
    }
}

Q2：2856. 删除数对后的最小数组长度

https://leetcode.cn/problems/minimum-array-length-after-pair-removals/

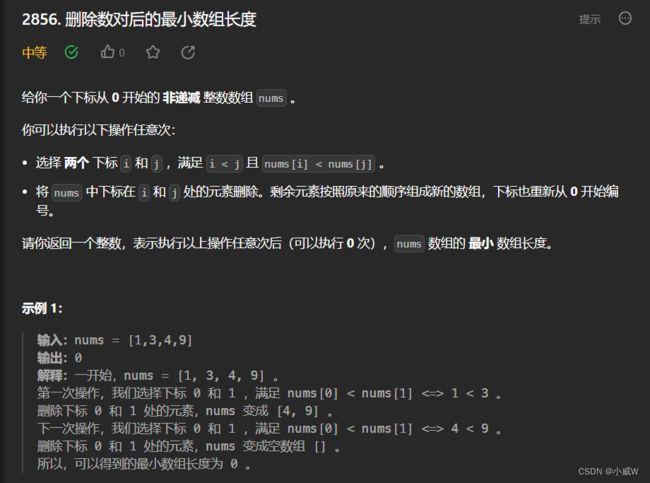
提示：
1 <= nums.length <= 10^5
1 <= nums[i] <= 10^9
nums 是 非递减 数组。

竞赛时代码——贪心+优先队列

首先贪心地想，能匹配就匹配。
但是对于样例 [2, 3, 5, 4] 来说，2 和 3 匹配之后，5 和 4就不能匹配了。
所以在 2 和 3 匹配之后，当枚举到 5 时，可以使用 5 替换掉 3，重新将 3 放入待匹配队列中。

具体算法如下：

---

使用两个优先队列维护已经被枚举过的数值。
pq1 维护等待匹配的较小数字，pq2 维护已经匹配过的较大数字。

分情况讨论：

1. 当前数字比 pq1 中的数字大时，就将 pq1 中最小的数字删除，两者完成配对，当前数字放入 pq2。
2. 当前 pq1 中没有数字，即前面没有元素等待配对时，将当前数字与 pq2 中最小的数字比较，如果 pq2 中的数字较小，就使用当前数字替换 pq2 中的数字与前面配对，同时 pq2 中这个最小的数字就多余了，将其放入 pq1 中等待后序的匹配。
3. 当前数字无法处理时，就放入 pq1 等待后面出现更大的数字时删除。

class Solution {
    public int minLengthAfterRemovals(List<Integer> nums) {
        int cnt = 0;    // 记录删除了几个数字
        // pq1记录较小的数字，pq2记录较大的数字
        PriorityQueue<Integer> pq1 = new PriorityQueue<>(), pq2 = new PriorityQueue<>();
        for (int x: nums) {
            // 如果当前数字比之前出现的 还没被删除过的数字 大
            if (!pq1.isEmpty() && x > pq1.peek()) {
                cnt += 2;
                pq1.poll();
                pq2.offer(x);
            } else {
                if (pq1.isEmpty() && !pq2.isEmpty() && x > pq2.peek()) {
                    // 如果较小的数字没有了 且 当前数字比已经删除的较大的数字大，就替换一下，将之前较大的数字放入较小的数字组中
                    pq1.offer(pq2.poll());
                    pq2.offer(x);
                } else pq1.offer(x);
            }
        }
        return nums.size() - cnt;
    }
}

Q3：6988. 统计距离为 k 的点对

https://leetcode.cn/problems/count-pairs-of-points-with-distance-k/

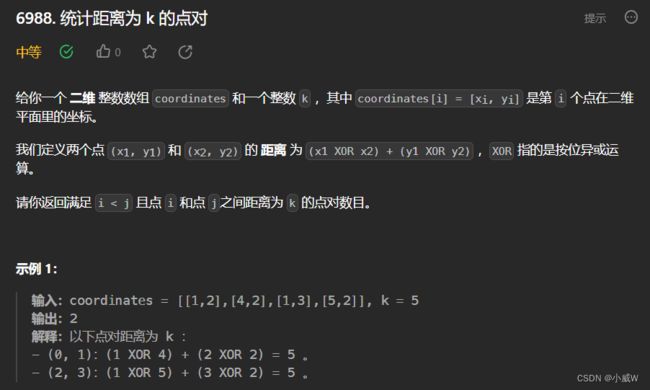
提示：
2 <= coordinates.length <= 50000
0 <= xi, yi <= 10^6
0 <= k <= 100

竞赛时代码——异或性质+哈希表

可以看到数据范围很怪，是 50000，而 k 的数据范围比较小，是 100。我们可以写一个时间复杂度是 $O(n\ast k)$ 的算法。

将已经枚举过的 x 和 y 放入哈希表中。
对于一个新的 x 和 y，他要和另外的坐标匹配之和为 k，最多有 k 中可能，即 —— 0 + k， 1 + (k - 1)，2 + (k - 2)，… ，k + 0。枚举每种情况即可。

根据异或的性质，有 x ^ (i ^ x) = i, y ^ ((k - i) & y) = k - i，因此与 坐标 (x, y) 可以匹配的坐标是 (i ^ x, (k - i) ^ y)，其中 i 的取值范围是 0 ~ k。

class Solution {
    public int countPairs(List<List<Integer>> coordinates, int k) {
        int ans = 0;
        Map<Integer, Map<Integer, Integer>> cnt = new HashMap<>();
        for (List<Integer> c: coordinates) {
            int x = c.get(0), y = c.get(1);
            // 枚举 x 和 y 异或取值分配的所有可能。
            for (int i = 0; i <= k; ++i) {
                ans += cnt.getOrDefault(i ^ x, new HashMap<>()).getOrDefault((k - i) ^ y, 0);
            }
            // 将当前坐标放入哈希表
            if (!cnt.containsKey(x)) cnt.put(x, new HashMap<>());
            cnt.get(x).merge(y, 1, Integer::sum);
        }
        return ans;
    }
}

更多有关异或的题目可见：异或/XOR部分问题汇总

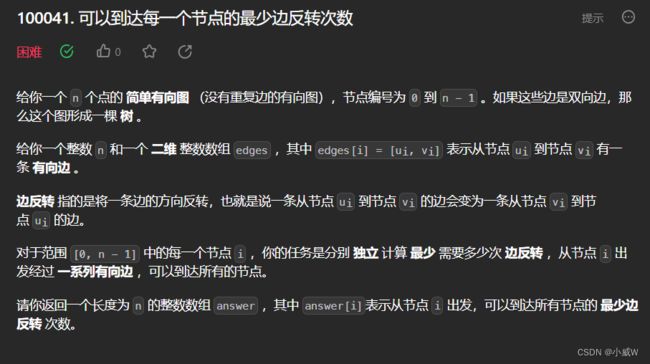
Q4：100041. 可以到达每一个节点的最少边反转次数

提示：
2 <= n <= 10^5
edges.length == n - 1
edges[i].length == 2
0 <= ui == edges[i][0] < n
0 <= vi == edges[i][1] < n
ui != vi
输入保证如果边是双向边，可以得到一棵树。

竞赛时代码——换根DP

第一次 dfs 求各个节点向下需要的反转次数。
第二次 dfs 求答案。

class Solution {
    List<Integer>[] g;
    Set<Integer>[] t;
    int n;
    // 答案，该节点往下传递反转的数量，
    int[] ans, cnt;
    
    public int[] minEdgeReversals(int n, int[][] edges) {
        this.n = n;
        ans = new int[n];
        cnt = new int[n];
        g = new ArrayList[n];
        t = new HashSet[n];
        Arrays.setAll(g, e -> new ArrayList<>());
        Arrays.setAll(t, e -> new HashSet<>());
        
        for (int[] e: edges) {
            int x = e[0], y = e[1];
            g[x].add(y);
            g[y].add(x);
            t[x].add(y);
        }
        
        dfs1(0, -1);        // 求cnt
        ans[0] = cnt[0];
        dfs2(0, -1);        // 求ans
        
        return ans;
    }
    
    public void dfs1(int x, int fa) {
        for (int y: g[x]) {
            if (y != fa) {
                dfs1(y, x);         // 先求cnt[y]
                if (!t[x].contains(y)) cnt[x]++;    // 如果x不能往y走,就+1
                cnt[x] += cnt[y];   
            }
        }
    }
    
    public void dfs2(int x, int fa) {
        for (int y: g[x]) {
            if (y != fa) {
                ans[y] = ans[x];    // 两者的差别只取决于x和y之间边的情况
                if (t[x].contains(y) && !t[y].contains(x)) ans[y]++;
                else if (!t[x].contains(y) && t[y].contains(x)) ans[y]--;
                dfs2(y, x);
            }
        }
    }
}

更多关于换根DP可见：
【算法】换根DP
【LeetCode每日一题合集】2023.7.10-2023.7.16（dfs & 换根DP）

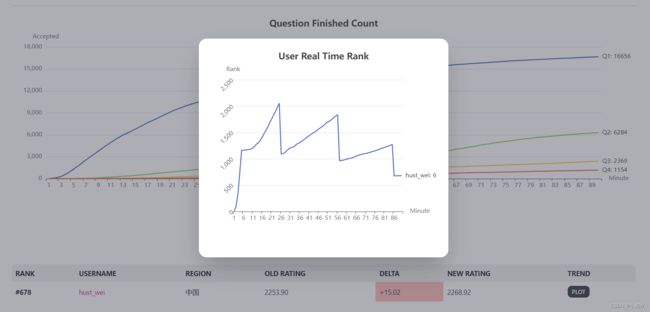
成绩记录

靠自己 AK 了！