蓝桥杯 题库 简单 每日十题 day3
01 约数个数
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
1200000 有多少个约数(只计算正约数)。
解题思路
枚举,从1开始一直到1200000本身都作为1200000的除数,如果可以整除,则是它的约数
#include 02 平方和
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
小明对数位中含有 2、0、1、9 的数字很感兴趣,在 1 到 40 中这样的数包括 1、2、9、10 至 32、39 和 40,共 28 个,他们的和是 574,平方和是 14362。
注意,平方和是指将每个数分别平方后求和。
请问,在 1 到 2019 中,所有这样的数的平方和是多少?
#include 03 星期一
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
整个 20 世纪(1901 年 1 月 1 日至 2000 年 12 月 31 日之间),一共有多少个星期一?(不要告诉我你不知道今天是星期几)
#include04 猴子分香蕉
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
5 只猴子是好朋友,在海边的椰子树上睡着了。这期间,有商船把一大堆香蕉忘记在沙滩上离去。
第 1 只猴子醒来,把香蕉均分成 5 堆,还剩下 1 个,就吃掉并把自己的一份藏起来继续睡觉。
第 2 只猴子醒来,把香蕉均分成 5 堆,还剩下 2 个,就吃掉并把自己的一份藏起来继续睡觉。
第 3 只猴子醒来,把香蕉均分成 5 堆,还剩下 3 个,就吃掉并把自己的一份藏起来继续睡觉。
第 4 只猴子醒来,把香蕉均分成 5 堆,还剩下 4 个,就吃掉并把自己的一份藏起来继续睡觉。
第 5 猴子醒来,重新把香蕉均分成 5 堆,哈哈,正好不剩!
请计算一开始最少有多少个香蕉。
#include05 合数个数
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
一个数如果除了 1 和自己还有其他约数,则称为一个合数。例如:1,2,3 不是合数,4, 6是合数。
请问从 1 到 2020 一共有多少个合数。
#include 06 玩具蛇
题目描述
本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。
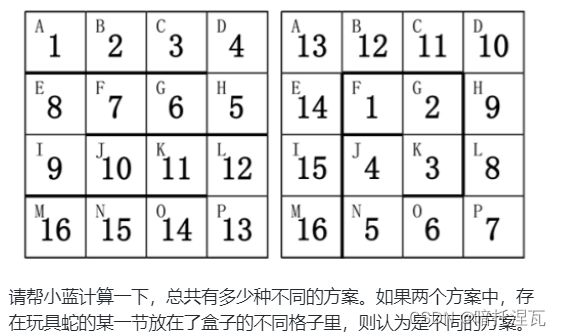
小蓝有一条玩具蛇,一共有 16 节,上面标着数字 1 至 16。每一节都是一个正方形的形状。相邻的两节可以成直线或者成 90 度角。
小蓝还有一个 4 × 4 的方格盒子,用于存放玩具蛇,盒子的方格上依次标着字母 A 到 P 共 16 个字母。
小蓝可以折叠自己的玩具蛇放到盒子里面。他发现,有很多种方案可以将玩具蛇放进去。
下图给出了两种方案:
玩具蛇思路:难点是如何用代码抽象出来题目的条件,其实我们可以自己模拟一下放玩具蛇的过程,相邻的节数满足直线和九十度,可以抽象成,下一节的放置是上一节模拟上下左右移动的过程,那么这就是一个dfs的模板题了
#include 07 矩形切割
#include08 美丽的 2
#include 09 一步之遥

题意
小明有两种操作:操作1,使数字加97,操作2,使数字减127,问小明把0变成1至少要几步?
分析
由贝祖定理可知给予二个整数a、b,必存在整数x、y使得ax + by = gcd(a,b) ,且存在x < b, y < a满足等式。因为gcd(97, 127) = 1,所以可以断定小明可以把0变成1,并且步数在97 + 127步之内。只需要设计一个O(n^2)复杂度的算法即可满足需求。
解法
枚举操作1和操作2的次数,若结果刚好为1,记录为可能答案,在所有可能答案中选一个最小值即可。
提高
扩展欧几里得算法可以快速求得x和y的值。时间复杂度O log(min(a,b))
详见连接 https://blog.csdn.net/destiny1507/article/details/81750874
#include 法二
#include10 煤球数目
#include