树状数组(1.单点修改,区间查询 2.区间修改,单点查询)
部分转载及其图片引用自树状数组 数据结构详解与模板。
目录
- 前言
- 树状数组 1:单点修改,区间查询
-
- 题目描述
- lowbit函数
- 单点更新
- 区间查询
-
- 前缀和
- C++代码
- 树状数组 2:区间修改,单点查询
-
- 题目描述
- 区间更新
-
- 差分
- 单点查询
- C++代码
前言
对于这样一个问题:给定数组a,有两种操作,第一个操作是使第i个数加上c,即a[i] + c;第二个
操作是查询区间 [L, R] 中各个数的累加和即a[L] + a[L + 1] + ... + a[R]。
那么,朴素做法的话就是对于操作一使得a[i] += c,对于操作二遍历一遍从L到R,然后各元素依次加上,这样做的时间复杂度分别为 O(1) 和 O(n) 。也很容易想到利用前缀和来优化一下,但最终也会发现,虽然操作二的复杂度优化为 O(1) 了,但是在操作一上修改前缀和数组需要的复杂度却变为了 O(n) 。
所以这时候提出了树状数组的存储数据的结构,使得对于上面两个操作,复杂度均为 O(logN)。
下面便是树状数组的二叉树形式:
假设对于a[]数组,它对应到的树为另一数组tree[],那么第i个数a[i]的意义就是结点tree[i]。
标记为灰色的节点实际已被上层覆盖,不占据空间。

注意:任意结点tree[i]中存储的数据是所有子节点的和这句话很关键,它是优化更新和查询操作中循环次数的重要依据。
下面是二进制版本,能看到(绿色箭头的指向)
更新过程是每次加了个二进制的低位1(101+1 ->110, 110 + 10 -> 1000, 1000 + 1000 -> 10000)
查询过程每次就是去掉了二进制中的低位1(1111 - 1 -> 1110, 1110 - 10 -> 1100, 1100 - 100 -> 1000)

树状数组 1:单点修改,区间查询
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 x x x
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n , m n,m n,m,分别表示该数列数字的个数和操作的总个数。
第二行包含 n n n 个用空格分隔的整数,其中第 i i i 个数字表示数列第 i i i 项的初始值。
接下来 m m m 行每行包含 3 3 3 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 x x x 个数加上 k k k -
2 x y含义:输出区间 [ x , y ] [x,y] [x,y] 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 2 2 2 的结果。
样例
样例输入
5 5
1 5 4 2 3
1 1 3
2 2 5
1 3 -1
1 4 2
2 1 4
样例输出
14
16
提示
【数据范围】
对于 30 % 30\% 30% 的数据, 1 ≤ n ≤ 8 1 \le n \le 8 1≤n≤8, 1 ≤ m ≤ 10 1\le m \le 10 1≤m≤10;
对于 70 % 70\% 70% 的数据, 1 ≤ n , m ≤ 1 0 4 1\le n,m \le 10^4 1≤n,m≤104;
对于 100 % 100\% 100% 的数据, 1 ≤ n , m ≤ 5 × 1 0 5 1\le n,m \le 5\times 10^5 1≤n,m≤5×105。
样例说明:
故输出结果14、16。
lowbit函数
由于更新和查询过程中,任一结点x的下一个位置都与其二进制表示中最低位的1有关系,所以定义lowbit(x)是取出x的最低位1。
int lowbit(int x){ return x & (-x); }
单点更新
继续看开始给出的图
此时如果我们要更改A[1]
则有以下需要进行同步更新
1(001) tree[1]+=A[1]
lowbit(1)=001 1+lowbit(1)=2(010) tree[2]+=A[1]
lowbit(2)=010 2+lowbit(2)=4(100) tree[4]+=A[1]
lowbit(4)=100 4+lowbit(4)=8(1000) tree[8]+=A[1]
所以得出结论是:更新点x后,还需要不停往上更新包含了x的父结点直到更新至根节点n为止,而父结点的下标由x + lowbit(x)而来。
void update(int x, int k){
while(x <= n){
tree[x] += k;
x += lowbit(x); //x的父节点
}
}
区间查询
前缀和
借助前缀和的思想,求 [L,R] 区间的Σ可以利用R的前缀和减去L - 1的前缀和,而这个前缀和的求法如下:
举个例子 x=5
tree[4]=A[1]+A[2]+A[3]+A[4];
tree[5]=A[5];
可以推出: sum(i = 5) ==> tree[4]+tree[5];
序号写为二进制: sum(101)=tree[(100)]+tree[(101)];
第一次101,减去最低位的1就是100。
其实也就是单点更新的逆操作
int getsum(int x){ //先求前缀和
int sum = 0;
while(x){
sum += tree[x];
x -= lowbit(x);
}
return sum;
}
int query(int x, int y){ //性质
return getsum(y) - getsum(x - 1);
}
C++代码
#include 树状数组 2:区间修改,单点查询
题目描述
如题,已知一个数列,你需要进行下面两种操作:
-
将某区间每一个数加上 x x x;
-
求出某一个数的值。
输入格式
第一行包含两个整数 N N N、 M M M,分别表示该数列数字的个数和操作的总个数。
第二行包含 N N N 个用空格分隔的整数,其中第 i i i 个数字表示数列第 $i $ 项的初始值。
接下来 M M M 行每行包含 2 2 2 或 4 4 4个整数,表示一个操作,具体如下:
操作 1 1 1: 格式:1 x y k 含义:将区间 [ x , y ] [x,y] [x,y] 内每个数加上 k k k;
操作 2 2 2: 格式:2 x 含义:输出第 x x x 个数的值。
输出格式
输出包含若干行整数,即为所有操作 2 2 2 的结果。
样例
样例输入
5 5
1 5 4 2 3
1 2 4 2
2 3
1 1 5 -1
1 3 5 7
2 4
样例输出
6
10
提示
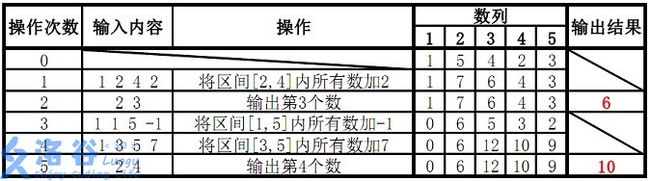
样例 1 解释
故输出结果为 6、10。
数据规模与约定
对于 30 % 30\% 30% 的数据: N ≤ 8 N\le8 N≤8, M ≤ 10 M\le10 M≤10;
对于 70 % 70\% 70% 的数据: N ≤ 10000 N\le 10000 N≤10000, M ≤ 10000 M\le10000 M≤10000;
对于 100 % 100\% 100% 的数据: 1 ≤ N , M ≤ 500000 1 \leq N, M\le 500000 1≤N,M≤500000, 1 ≤ x , y ≤ n 1 \leq x, y \leq n 1≤x,y≤n,保证任意时刻序列中任意元素的绝对值都不大于 2 30 2^{30} 230。
区间更新
差分
其实对于前面的两种操作,发现用的还是一个前缀和的思想,为了便于求出 [L,R] 区间的累加和,通过
树状数组求出两个前缀和后作差便轻易得出。那么按照同样的思路,为了便于对整个区间进行修改,可
以考虑差分的思想,使树状数组存的是关于原数组a(虽然不会用上)的差分,即
tree[i] = a[i] - a[i - 1]
于是每次在对区间更新时只需将相关的父子结点 “打上标记” 便实现,而要查询某个点i,只需求一
遍前缀和(a[i] = tree[1] + tree[2] + .. + tree[i])即可。
void insert(ll i, ll k){ //差分数组上打标记
while (i <= n){
tree[i] += k;
i += lowbit(i);
}
}
void update(ll x, ll y, ll k){
insert(x, k), insert(y + 1, -k);
}
单点查询
ll query(ll x){ //求前缀和,跟getsum一样
ll sum = 0;
while(x){
sum += tree[x];
x -= lowbit(x);
}
return sum;
}
C++代码
#include 对于区间修改和区间查询,很适合考虑线段树来做,
线段树(区间修改,区间合并)