直方图规定化——GML和SML映射规则
GML和SML原理
GML规定化(组映射)
先列出图像灰度值i,j,计算原始直方图Pr(i),列出规定直方图Pz(j),计算原始累计直方图Pi和规定累计直方图Pj,然后按照Pj到Pi寻找最接近的值存储为j,当满足给定的值多于一个时,按惯例取最小值。确定变换关系为i->j,最后列出匹配直方图P(j)。
SML规定化(单映射)
先列出图像灰度值i,j,计算原始直方图Pr(i),列出规定直方图Pz(j),计算原始累计直方图Pi和规定累计直方图Pj,然后按照Pi到Pj寻找最接近的值存储为j,当满足给定的值多于一个时,按惯例取最小值。确定变换关系为i->j,最后列出匹配直方图P(j)。
映射结果与分析
GML(组映射)映射结果
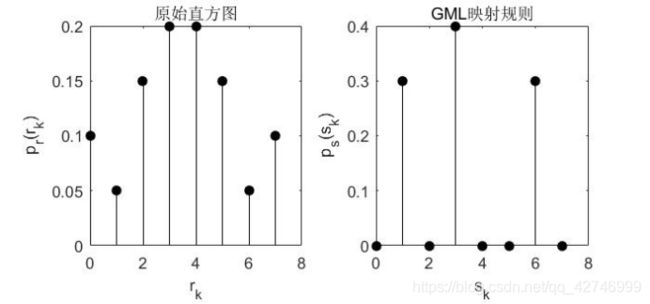
GML映射分析
先列出图像灰度值i,j,计算原始直方图Pr(i),列出规定直方图Pz(j),计算原始累计直方图Pi和规定累计直方图Pj,然后按照Pj到Pi寻找最接近的值存储为j,当满足给定的值多于一个时,按惯例取最小值。确定变换关系为i->j,最后列出匹配直方图P(j)。
SML(单映射)映射结果
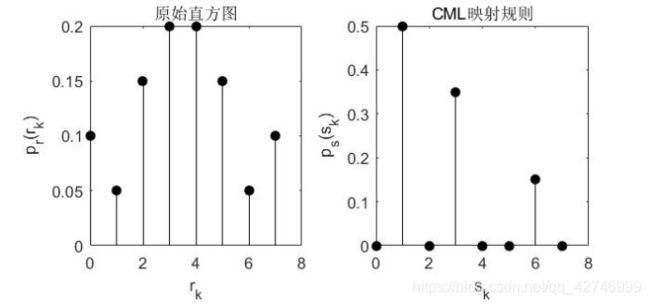
SML映射分析
先列出图像灰度值i,j,计算原始直方图Pr(i),列出规定直方图Pz(j),计算原始累计直方图Pi和规定累计直方图Pj,然后按照Pi到Pj寻找最接近的值存储为j,当满足给定的值多于一个时,按惯例取最小值。确定变换关系为i->j,最后列出匹配直方图P(j)。
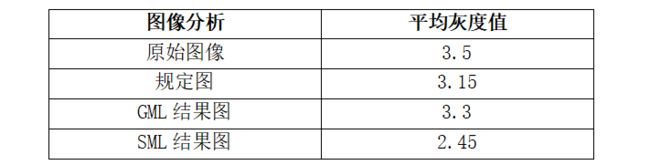
两种映射方法对比分析
代码
GML映射
%Write by 长安 Rjex
clc ,clear all
A = [0.1 0.05 0.15 0.2 0.2 0.15 0.05 0.1]; %原直方图矩阵
C = [0 0.3 0 0.45 0 0 0.25 0]; %规定直方图矩阵
F=zeros(1,size(A,2)); %规定化后直方图矩阵
for i = 1:size(A,2) %B为A的累计直方图矩阵
if i == 1
B(i) = A (i);
else
B(i) = B(i-1) + A(i);
end
end
for i = 1:size(C,2)
if i == 1
D(i) = C (i);
else
D(i) = D(i-1) + C(i);
end
end
min=1;
flag2 = 1;
for i = 1:size(D,2)
if C(i)~=0
for j = flag2:size(B,2)
t=abs(D(i)-B(j));
if(t<min)
min=t; %min为求差最小绝对值
flag=j; %flag为所求的最小绝对值下标
end
end
for k = flag2:flag
E(k) = i; %E为GML映射规则矩阵
end
flag2 = flag+1;
min=1;
end
end
for i = 1:size(E,2)
F(E(i))=F(E(i))+A(i);
end
j=1:size(A,2);
subplot(1,2,1),stem(j-1,A(j),'fill','black'),title('原始直方图'),xlabel('r_{k}'),ylabel('p_{r}(r_{k})');
subplot(1,2,2),stem(j-1,F(j),'fill','black'),title('GML映射规则'),xlabel('s_{k}'),ylabel('p_{s}(s_{k})');
SML映射
%Write by 长安 Rjex
clc ,clear all
A = [0.1 0.05 0.15 0.2 0.2 0.15 0.05 0.1]; %原直方图矩阵
C = [0 0.3 0 0.45 0 0 0.25 0]; %规定直方图矩阵
F=zeros(1,size(A,2)); %规定化后直方图矩阵
for i = 1:size(A,2) %B为A的累计直方图矩阵
if i == 1
B(i) = A (i);
else
B(i) = B(i-1) + A(i);
end
end
for i = 1:size(C,2) %D为C的累计直方图矩阵
if i == 1
D(i) = C (i);
else
D(i) = D(i-1) + C(i);
end
end
min=1;
flag = 1;
for i = 1:size(B,2)
for j = 1:size(D,2)
if C(j)~=0
t=abs(B(i)-D(j));
if(t<min)
min=t; %min为求差最小绝对值
flag=j; %flag为所求的最小绝对值下标
end
end
end
E(i) = flag; %E为CML映射规则矩阵
min=1;
end
for i = 1:size(E,2) %F为规定化后直方图矩阵
F(E(i))=F(E(i))+A(i);
end j=1:size(A,2);
subplot(1,2,1),stem(j-1,A(j),'fill','black'),title('原始直方图'),xlabel('r_{k}'),ylabel('p_{r}(r_{k})');
subplot(1,2,2),stem(j-1,F(j),'fill','black'),title('CML映射规则'),xlabel('s_{k}'),ylabel('p_{s}(s_{k})');