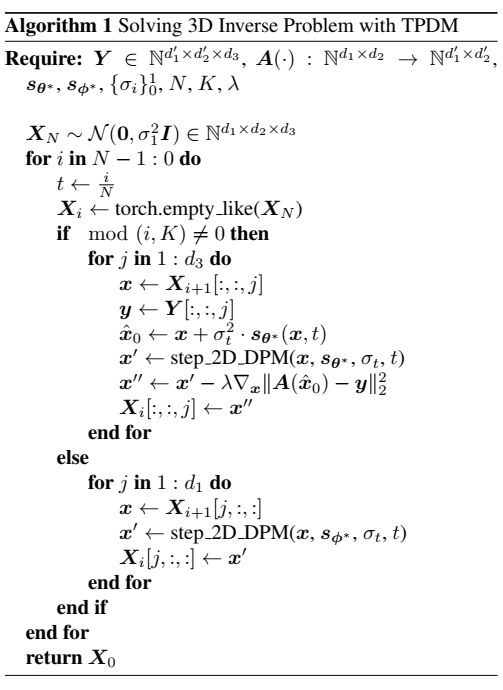Improving 3D Imaging with Pre-Trained Perpendicular 2D Diffusion Models

使用预先训练的垂直 2D 扩散模型改进 3D 成像

论文链接：https://arxiv.org/abs/2303.08440

项目链接：https://github.com/hyn2028/tpdm

Abstract

扩散模型由于其众多的优点已经成为一种流行的图像生成和重建方法。然而，大多数基于扩散的逆问题解决方法只处理2D图像，甚至最近发表的3D方法也没有充分利用3D分布先验。为了解决这个问题，我们提出了一种新的方法，使用两个垂直的预训练二维扩散模型来解决三维逆问题。通过将三维数据分布建模为二维分布在不同方向上的切片的乘积，我们的方法有效地解决了维度灾难。实验结果表明，我们的方法对三维医学图像重建任务非常有效，包括MRI z轴超分辨率，压缩感知MRI和稀疏视图CT。我们的方法可以生成适合医疗应用的高质量体素体。

1. Introduction

扩散概率模型(diffusion probabilistic model, DPM)使用神经网络学习对数概率分布$\nabla x\log p_{data}(x)$的梯度，也称为分数函数。通过使用Langevin动力学[38]或使用学习分数函数求解逆随机微分方程(SDE)进行采样[40]。

DPM自推出以来，已经成为图像领域的领先生成模型[37,15,40]，在实现最先进的性能方面超越了GAN等其他模型[10,30]。扩散模型与条件反射训练的融合是一个值得注意的协同作用，它构成了文本引导图像生成领域的基础框架[30,32,29]。此外，它的广泛适用性扩展到新的领域，如脑视觉解码[3,41]。在音频[28,22,18]、视频[2,36,26]、辐射场[27,35]和图形[43,17]等其他领域，它也被作为生成模型进行探索。

尽管由于在多个时间步上进行顺序采样而导致采样速度较慢，但扩散模型比其他生成模型具有显著的优势，包括采样时间的可扩展性。根据贝叶斯定理[10,16]，预训练分数函数模型可以用于不需要再训练的条件抽样。这种基于条件抽样的反问题解决方法可以解释为具有扩散生成先验的后验抽样。因此，它有效地避免了监督似然优化方法的偏差和回归均值现象。在适当的时候，基于扩散的反问题解决方法范式[40,20,7,5,4,39,6,45]已经上升到研究领域的前沿，成为一种最先进的技术。

大多数当代基于扩散的反问题求解方法都集中在二维应用上。然而，最近提出了一种名为DiffusionMBIR的方法[6]来解决医学成像中的3D逆问题。在DiffusionMBIR中，在主xy平面上训练的扩散模型被用作先验，生成先验被基于模型的先验增强，即总变异(TV)，以增强相邻切片(Z-axis)的平滑性。虽然这种方法对各种任务都很有效，但它仍然有局限性，因为它没有完全了解数据的3D先验分布。更具体地说，TV先验只施加来自有限差分算子的局部依赖，而真正的3D先验应该模拟全局依赖。

为了克服这一限制，我们提出了一种新的3D生成方法，称为两个垂直的2D扩散模型(TPDM)。TPDM充分利用了三维生成先验，通过对二维构成要素的乘积分布建模三维数据分布，而不依赖于基于模型的先验。这种方法允许TPDM仅使用两个2D扩散模型有效地学习3D先验：在xy平面上操作的主模型和学习yz平面的辅助模型。与之前的DiffusionMBIR方法不同，TPDM可以对3D结构的全局依赖性进行建模，并且消除了强加TV约束所需的子优化方案的需要。值得一提的是，与专为逆问题求解而设计的 DiffusionMBIR 不同，TDPM 是完全通用的 3D 生成模型，可用于条件采样和无条件采样。

在本文中，TPDM已经在MRI z轴(即垂直轴)超分辨率(MR-ZSR)，压缩感知MRI (CS-MRI)和稀疏视图CT (SV-CT)等各种3D医学成像重建问题中进行了测试，并与现有方法相比产生了最先进的结果。特别是，据我们所知，我们已经在技术上和临床上首次成功尝试了基于扩散模型的MR-ZSR(图2)。我们还证明了TPDM可以作为纯生成模型生成非常高质量的完整3D体素(图7)。我们的贡献可以总结如下：

1. 我们开发了一种新颖、简单、有效的方法，以完全无监督的方式解决了两个垂直的二维扩散模型作为三维先验的三维体积逆问题，而不需要重新训练。

2. 我们将其应用于各种医学成像重建问题，并取得了最知名的性能。特别是，TPDM在基于扩散模型的MR-ZSR的第一次尝试中取得了成功。

3. 最后，我们证明了TPDM也可以作为3D生成模型，生成高质量的3D体素体。

2. Background

2.1. 基于分数的扩散模型

扩散模型[37,15,40]是一个模型族，它定义了一个对原始数据逐渐加噪的过程，称为前向过程，并通过执行该加噪过程的学习反向过程来表达生成过程。其中，Song等人[40]引入的基于分数的扩散模型通过以下Ito随机微分方程(SDE)来定义正向过程。在整个扩散过程中，数据$x$可以用$x(t)=x_t$表示，连续时间指标$t\in [0,1]$。$x_0\sim p_{data}$为原始数据分布，$x_1\sim p_0$为预定义的先验分布。
$$d\mathbf{x}=\mathbf{f}(\mathbf{x},t)dt+g(t)d\mathbf{w},\text{\hspace{1em}(1)}$$
式中函数$f:{\mathbb{R}}^d\times \mathbb{R}\to {\mathbb{R}}^d$为漂移函数，函数$g:\mathbb{R}\to \mathbb{R}$为扩散系数。$w$是标准维纳过程，也称为布朗运动。公式(1)的逆时SDE可表示为[1,40]：
$$dx=[\mathbf{f}(\mathbf{x},t)-g(t{)}^2{\nabla }_{\mathbf{x}t}\log p({\mathbf{x}}_t)]dt+g(t)d\bar{\mathbf{w}}\text{\hspace{1em}(2)}$$
其中$\bar{w}$也是标准的维纳过程。

为了求解生成过程的逆时SDE，需要一个与时间相关的得分函数$\nabla x_t\log p(x_t)$，可以通过去噪得分匹配(DSM) 训练基于神经网络的得分函数估计器$s_{\theta }$来获得 目标 [44, 40]：
$$\underset{\mathbf{\theta }}{\min }{\mathbb{E}}_{{\mathbf{x}}_t|{\mathbf{x}}_0,{\mathbf{x}}_0}[\Vert {\mathbf{s}}_{\mathbf{\theta }}(\mathbf{x}(t),t)-{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|{\mathbf{x}}_0){\Vert }_2^2]\text{\hspace{1em}(3)}$$
设$f(x,t)=0,g(t)=\sqrt{\frac{d[{\sigma }^2(t)]}{dt}}$，加上正时变递增噪声标度函数$\sigma (t)$，我们实现了variance exploding SDE (VE-SDE)。用DSM目标训练的分数网络代替分数函数，可以有效地解决VE-SDE的采样过程。

2.2. 扩散后验抽样

扩散后验抽样(Diffusion posterior sampling, DPS)是Chung等人[5]提出的以扩散模型作为先验来解决一般噪声逆问题的最新方法之一。一般考虑正演模型的逆问题可以定义为：
$$\mathbf{y}=\mathbf{A}({\mathbf{x}}_0)+\mathbf{n},\mathbf{y},\mathbf{n}\in {\mathbb{R}}^n,\mathbf{x}\in {\mathbb{R}}^d\text{\hspace{1em}(4)}$$
式中，$A$为前向测量函数，$n$为测量噪声。为了利用扩散先验求解逆问题，我们可以使用贝叶斯规则得到：
$$\begin{array}{rl}{\nabla }_{x_t}\log p(x_t|\mathbf{y})& ={\nabla }_{x_t}\log p({\mathbf{x}}_t)+{\nabla }_{x_t}\log p(\mathbf{y}|{\mathbf{x}}_t)\\ & \simeq s_{{\theta }^{\ast }}({\mathbf{x}}_t,t)+{\nabla }_{x_t}\log p(\mathbf{y}|{\mathbf{x}}_t).\end{array}\text{\hspace{1em}(5)}$$
尽管如此，由于$x_t$和$y$之间没有明确的关系，我们不能直接使用公式(5)。为了规避这个问题，[5]提出了一种近似，理论上保证了近似误差的上界：
$${\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\mathbf{x}}_t)\simeq {\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t)),\text{\hspace{1em}(6)}$$
其中：
$${\hat{x}}_0(x_t):=\mathbb{E}[x_0|x_t]=x_t+{\sigma }^2(t){\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t)\text{\hspace{1em}(7)}$$
为Tweedie去噪估计[11,21]。因此，当测量噪声为高斯噪声时，可以使用：
$${\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|\mathbf{y})\simeq {\mathbf{s}}_{{\mathbf{\theta }}^{\bullet }}({\mathbf{x}}_t,t)-\lambda {\nabla }_{{\mathbf{x}}_t}\Vert \mathbf{A}({\hat{\mathbf{x}}}_0({\mathbf{x}}_t))-\mathbf{y}{\Vert }_2^2.\text{\hspace{1em}(8)}$$

3. Two Perpendicular 2D Diffusion Model

3.1. 建模数据分布

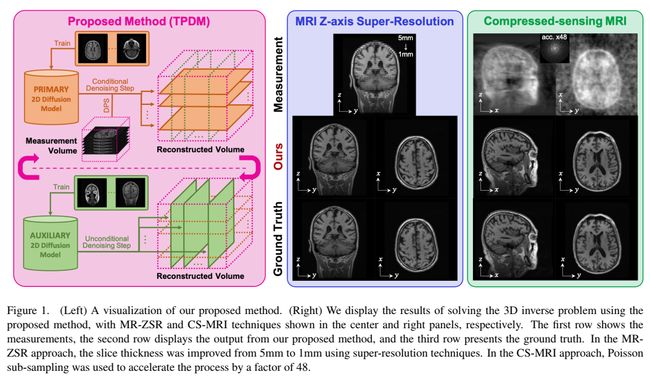
为了克服DiffusionMBIR的缺点，在这里我们描述了我们应用先验的方法，它比DiffusionMBIR更接近实际的3D分布。我们简单而有效的解决方案是，通过将三维数据分布建模为乘积分布，除了主要的二维扩散模型外，还使用在体积不同方向的二维切片上训练的辅助扩散模型来解决逆问题(图1)。这使我们能够在高维空间中有效地驱动扩散模型，就像在各种深度学习场景中利用分解方法来提高效率一样[33,13,12]。

具体来说，我们的建议是将数据分布建模为由：
$$\begin{array}{c}{p}_{\mathbf{\theta },\mathbf{\varphi }}(\mathbf{x})=q_{\mathbf{\theta }}^{(p)}(\mathbf{x}{)}^{\alpha }{q}_{\mathbf{\varphi }}^{(a)}(\mathbf{x}{)}^{\beta }/Z\\ =[q_{\mathbf{\theta }}^{(p)}({\mathbf{x}}_{[:,:,1]})q_{\mathbf{\theta }}^{(p)}({\mathbf{x}}_{[:,:,2]})\cdots q_{\mathbf{\theta }}^{(p)}({\mathbf{x}}_{[:,:,d_3]}){]}^{\alpha }\\ \times [q_{\mathbf{\varphi }}^{(a)}({\mathbf{x}}_{[1,:;]})q_{\mathbf{\varphi }}^{(a)}({\mathbf{x}}_{[2,:,:]})\cdots q_{\mathbf{\varphi }}^{(a)}({\mathbf{x}}_{[d_1,:,:]}){]}^{\beta }/Z,\end{array}\text{\hspace{1em}(9,10)}$$
其中$Z$为合适的归一化配分函数，$q_{\theta }^{(p)}(x)$为参数化θ的主模型建模的分布，$q_{\phi }^{(a)}(x)$为参数化φ的辅助模型建模的分布，对于$x\in {\mathbb{R}}^{d_1\times d_2\times d_3}$。此外，α， β根据重要性在两个分布之间引入权重。我们进一步假设$q_{\theta }^{(p)}$和$q_{\varphi }^{(a)}$都可以分解为独立的2D(切片)分布。

因此，当从先验分布$p_{\theta ,\varphi }(x)$中进行无条件采样时，我们可以直接使用
$$\begin{array}{c}{\nabla }_{x_t}\log p(x_t)=\alpha {\nabla }_{x_t}\log q^{(p)}(x_t)+\beta {\nabla }_{x_t}\log q^{(a)}(x_t)\\ =\alpha {\Sigma }_{i=1}^{d_3}{\nabla }_{x_t}\log q^{(p)}(x_{t,[:,:,i]})+\beta {\Sigma }_{i=1}^{d_1}{\nabla }_{x_t}\log q^{(a)}(x_{t,[i,:,:]})\\ \simeq \alpha {\Sigma }_{i=1}^{d_3}{s}_{{\theta }^{\ast }}^{3D}(x_{t,[:,:,i]})+\beta {\Sigma }_{i=1}^{d_1}{s}_{{\varphi }^{\ast }}^{3D}(x_{t,[i,:;]}),\end{array}\text{\hspace{1em}(11)}$$
其中，$x_{t,[i,:,:]}$和$x_{t,[:,:,j]}$分别表示$x_t$的第i和第j个x切片和第z切片，并且
$$\begin{array}{c}\{\begin{array}{l}{s}^{3D}({\mathbf{x}}_{t,[:,:,i]}{)}_{[:,:,i]}=s({\mathbf{x}}_{t,[:,:,i]})\\ {\mathbf{s}}^{3D}({\mathbf{x}}_{t,[:,:,i]}{)}_{[\text{otherwise}]}=0\end{array}\\ \{\begin{array}{ll}{s}^{3D}(x_{t,[i,:,:]}{)}_{[i,::]}=s(x_{t,[i,:,:]}& \\ s^{3D}(x_{t,[i,:,:]}{)}_{[\mathrm{otherwise}]}=0& \end{array}\end{array}\text{\hspace{1em}(12,13)}$$
由于我们的二维切片独立性假设，它使用了训练好的二维分数估计器$s(\cdot )$。但是，必须小心，因为简单地使用这种近似值计算量很大，因为每次迭代都必须计算两个正向传递。在这方面，我们建议通过交替更新来解决这个问题
$$\{\begin{array}{ll}\Sigma s_{{\mathbf{\theta }}^{\ast }}^{3D}({\mathbf{x}}_{t,[:,:,i]}),& \text{with }\mathbb{P}=\alpha /(\alpha +\beta )\\ \Sigma s_{{\mathbf{\varphi }}^{\ast }}^{3D}({\mathbf{x}}_{t,[i,:,:]}),& \text{with }\mathbb{P}=\beta /(\alpha +\beta )\end{array}\text{\hspace{1em}(14)}$$
其中P表示要执行的每一步的概率。公式(14)可以在有规律的结构间隔或随机方式中实现，我们将在3.2节中详细讨论。

最后，为了求解逆问题，我们可以利用以下结果：
$$\begin{array}{rl}{\nabla }_{{\mathbf{x}}_t}\log p({\mathbf{x}}_t|\mathbf{y})& \simeq \alpha {\nabla }_{{\mathbf{x}}_t}\log q^{(p)}({\mathbf{x}}_t)\\ & +\beta {\nabla }_{{\mathbf{x}}_t}\log q^{(a)}({\mathbf{x}}_t)+{\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{\mathbf{x}}}_0({\mathbf{x}}_t)),\end{array}\text{\hspace{1em}(15)}$$
其中，与公式(14)中的无条件抽样相似，简化为：
$$\{\begin{array}{ll}\Sigma s_{\mathbf{\theta }\bullet }^{3D}(x_{t,[:::i]})+{\gamma }_t{\nabla }_{{\mathbf{x}}_t}\log p(\mathbf{y}|{\hat{x}}_0(x_t)),& \text{with }\mathbb{P}=\alpha /(\alpha +\beta )\\ \Sigma s_{{\mathbf{\varphi }}^{\ast }}^{3D}(x_{t,[i,::]}),& \text{with }\mathbb{P}=\beta /(\alpha +\beta )\end{array}\text{\hspace{1em}(16)}$$
其中${\gamma }_t$是步长，它也吸收了由$\alpha$和$\beta$引起的权重因子。

3.2. 利用TPDM解决三维重建问题

TPDM的训练通过训练主2D扩散模型和辅助2D扩散模型来完成(算法见附录A.1)。主要的二维扩散模型$s_{\theta }^{\ast }$在求解反问题时选择一个合适的平面，并将三维体的切片图像训练到相应的平面。如CS-MRI、SV-CT为轴向面，MR-ZSR为矢状面或冠状面。一个辅助的二维扩散模型$s_{\phi }^{\ast }$通过选择两个剩余的平面中的一个来训练。

为了解决反问题，使用训练好的TPDM对一个时间步去噪的每一步交替进行条件采样(算法1)。

虽然为了清晰起见，这些算法是单独提出的，但为了提高计算效率，它们可以批处理。在每个去噪步骤中，我们使用初级扩散模型$s_{\theta }^{\ast }$来约束测量值y的一致性，并使用DPS对图像进行采样[5]。超参数λ控制测量一致性的强度。辅助扩散模型$s_{\varphi }^{\ast }$用于纠正由主要扩散模型引起的批方向不一致。我们使用整数超参数K来调整两个模型的贡献(对于K的非整数值，参见附录A.2)。例如，当K=4时，主模型和辅助模型对图像生成的贡献比例分别为3:1。

4. Methods

在本文中，我们研究了TPDM的各种应用，包括医学领域的逆问题，如1)MRI z轴(垂直轴)超分辨率(MRZSR)， 2)压缩感知MRI (CS-MRI)和3)稀疏视图CT (SV-CT)。除了解决应用扩散模型条件采样的三维逆问题外，TPDM还用于生成脑MRI中无条件高保真三维体素体积。

4.1. 数据集

MR-ZSR, CS-MRI和3D体素生成任务使用我们的IRB批准的内部脑MRI图像数据集(即BMR-ZSR-1mm和BMR-ZSR-5mm)。详细信息请参见附录B.1。所有的体量都是256×256×256立方体的形状和标准的3T t1加权图像。BMR-ZSR-1mm，用于培训和回顾性评估，切片厚度为1mm。使用923卷(236288张2D图像)作为训练数据集，1卷作为回顾性切片厚度退化或CS-MRI子采样模拟的测试数据集。BMR-ZSR-5mm是在5mm切片厚度下获得的前瞻性数据集，用于MR-ZSR的前瞻性临床评价。

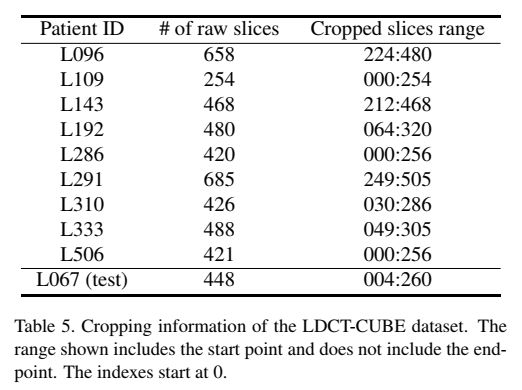
SV-CT任务使用AAPM 2016 CT低剂量大挑战中提供的公共CT数据集[25]。该数据集由总共10个体积的增强腹部CT组成。为了使体积成为256×256× 256的立方体，我们将xy平面的大小调整为256×256，并在z方向裁剪公共部分以使长度为256(即LDCT-CUBE数据集)。其中1卷作为回顾性测量模拟的测试数据集，其余9卷作为训练数据集。我们用于训练的数据只有 2304 个 2D 图像，因此即使训练数据很小，我们也可以展示可靠的性能。

4.2. 逆问题的测量模型

MR-ZSR。该任务的目标是将5mm层厚度MRI图像的超分辨率提高到1mm层分辨率，用于定量脑MR分析，如皮质厚度测量。考虑到MRI的切片选择过程，可以将z轴方向的相邻体素结合起来，进行平均运算，对正向测量核进行建模。例如，对于5mm到1mm切片的超分辨率，正演模型是对1mm切片图像进行降级的操作，方法是沿z轴方向对相邻的5个xy平面进行分组，并对每组进行平均，得到5mm切片图像。在这里，我们将要合并的组的z轴方向的像素数定义为合并大小(M)。

我们在创建回顾性退化MRI数据集(1mm→2,5mm)时使用了刚刚提出的前向核。在求解逆问题MR-ZSR时，我们还使用了DPS步骤中使用的略有不同的前向测量核。核类似于平均过程，但在平均时，除√M而不是除M，这是受到Song等[40]和Chung等[7]基于扩散模型的图像着色方法的启发。

CS-MRI和SV-CT。压缩感知MRI (CS-MRI)的前向测量核涉及在使用二维傅里叶变换将其转换为k空间后，对图像的每个切片应用二维子采样掩码。测量结果y在k空间域中给出。在稀疏视图CT (SV-CT)的情况下，前向测量核由稀疏视图CT采集场景确定，其中角度投影视图在稀疏角度集上进行次采样。测量是在正弦图空间中给出的。

4.3. DPM的训练和采样

在常用的模型设置和算法下，对MRI模型和CT模型进行训练和推断。构成TPDM的二维图像扩散模型采用NCSNPP[40]，采用VE-SDE，按照几何序列σ0=0.01 ~ σ1=378进行调度。所有输入在0到1之间归一化。在MR-ZSR问题中，使用YZ-plane (corononal)作为主模型，使用XY-plane (axial)作为辅助模型。在所有其他问题中，xy平面(轴向)用于主模型，YZ平面(冠状面)用于辅助模型。训练批大小为8,MRI模型和CT模型分别进行300K和100K次训练迭代。抽样阶段采用N=2000和预测校正抽样[40]方法。

4.4. 比较方法与评价

对于三维医学逆问题，我们的方法与DiffusionMBIR[6]、DPS[5]、MCG[7]、score-MRI[8]、score-CT[39]、L1-Wavelet[24]、FBPConvNet[19]和ADMM-TV进行了比较。DiffusionMBIR是解决一般3D逆问题的最先进方法，优于CS-MRI中的Score-MRI、DuDoRNet[47]、U-Net[31]和zero -fill等现有方法，优于SV-CT中的MCG、Lahiri等[23]、FBPConvNet和ADMM-TV等先前方法。由于MR-ZSR问题是一个新的尝试，没有基于扩散的方法被设计来专门解决它。采用峰值信噪比(PSNR)和结构相似性指数(SSIM)对回顾性测试数据集进行定量评价[46]。在三维体积中评估PSNR, SSIM测量每个切片方向(轴向、冠状面和矢状面)的二维切片结果的平均值。

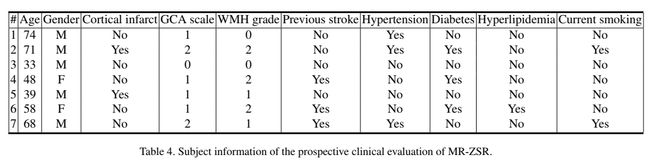
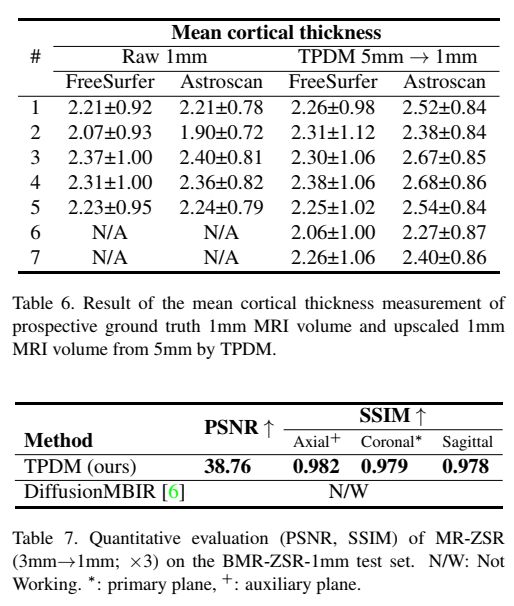
为了评估MR-ZSR的临床意义，7例缺血性脑卒中患者被纳入评估(BMR-ZSR-5mm)。皮质萎缩和白质高强度的视觉评估分别采用Global cortical atrophy scale[14]和Fazekas grade[34]。利用TDPM，将厚度为5mm的准标准t1加权图像重构为1mm图像。7例患者中有5例同时获得三维体积1mm T1加权图像和5mm T1加权图像。将升级后的T1加权图像获得的平均皮质厚度与1mm原始T1加权图像测量的平均皮质厚度进行比较，作为地面真值。使用FreeSurfer[42]和ATROSCAN (JLK Inc.， Seoul, Republic of Korea)基于Swin U-net[9]测量皮质厚度。

5. Experimental Results

5.1. MRI z轴超分辨率(MR-ZSR)

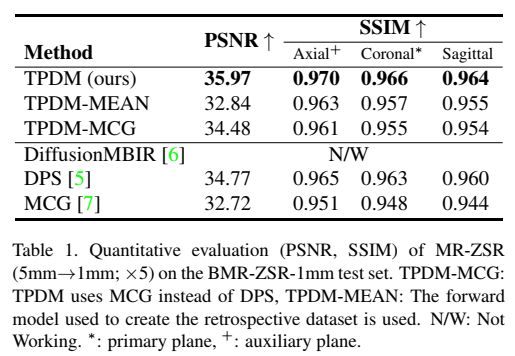
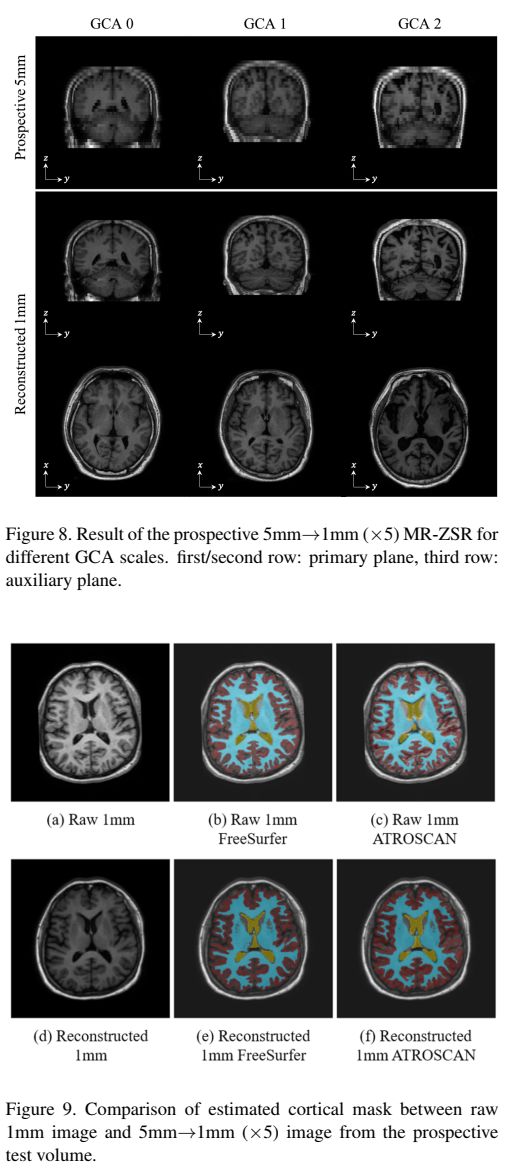
我们首先使用回顾性5mm测试数据集对主要用于临床的5mm切片进行MRI z轴×5超分辨率成像至1mm，结果见表1和图2。有关其他合并大小，请参见附录C.1。使用TPDM的MR-ZSR在定量上的结果优于任何其他基于扩散的2D/3D反问题解决方法[6,5,7]，并且在体积的任何切片方向上都没有出现伪影。此外，辅助模型的使用不仅提高了辅助方向的切片质量，而且还具有改善整个切片方向细节的效果(见图2的©和(d))。

值得注意的是，众所周知，性能最高的一般线性3D逆问题求解器DiffusionMBIR[6]根本不适用于我们定制设计的MR-ZSR正向测量核。这一问题是由总变差损失项引起的，总变差损失项是DiffusionMBIR中保证批方向一致性的关键点损失项。

作为TPDM的正演模型，在合并切片时，将切片之和除以√M (TPDM)而不是使用N (TPDM- mean)，可以获得更好的结果。此外，作为对主模型生成施加测量一致性约束的方法，TDPM与DPS (TPDM)的预后优于TDPM合并MCG (TPDM-MCG)，这与[5]一致。

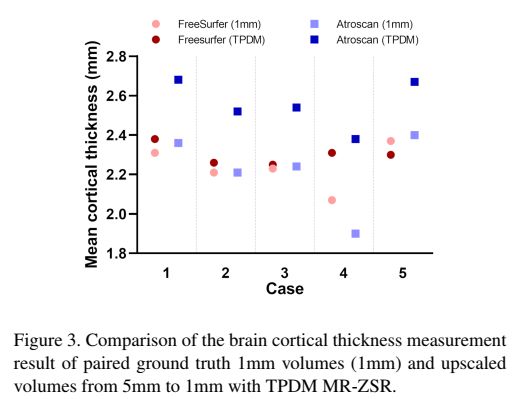
重建1mm图像中测量的皮质掩膜与FreeSurfer(附录C.1)在原始1mm图像中估计的掩膜相当，平均差异为0.06±0.11(配对t检验，p=0.28)，说明TDPM重建的T1图像可靠地用于临床常规T1图像无法测量的皮质厚度测量(图3)。通过ATROSCAN测量皮质厚度时，重建1mm图像的皮质掩膜大于原始1mm图像的皮质掩膜；平均差异为0.34±0.08(配对t检验；p < 0.001)。尽管如此，对于临床应用来说，这种差异是在相当合理的范围内的。

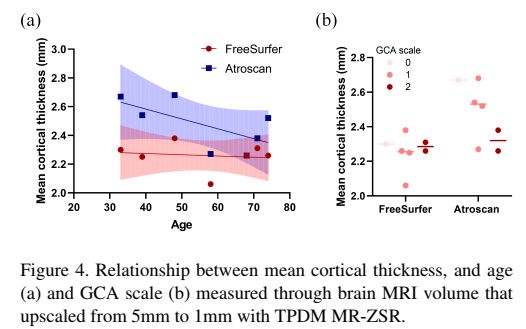
尽管在重建的T1图像中，Freesurfer的年龄依赖性皮质厚度下降并不明显，但在ATROSCAN中可以清楚地观察到其总体趋势，如点阵图所示(图4A)。在全球皮层萎缩量表(Global Cortical Atrophy scale, GCA)中也观察到类似的趋势，其中ATROSCAN的皮质厚度相关性优于FreeSurfer(图4B)，尽管由于样本小，两种量表之间的差异并不显著(p分别=0.82和0.22)。

常规脑MR T1图像通常为5mm厚度，以节省扫描时间。本研究的结果表明，TDPM模型可以显著扩大容量测量的合格图像池，这将有助于认知衰退的研究。这一点尤其重要，因为目前常规的5mm采集方案不足以进行此类研究。进一步的研究需要更大的样本量和更多样化的人群来充分证明TDPM图像重建的临床意义。

5.2. 压缩感知MRI (CS-MRI)

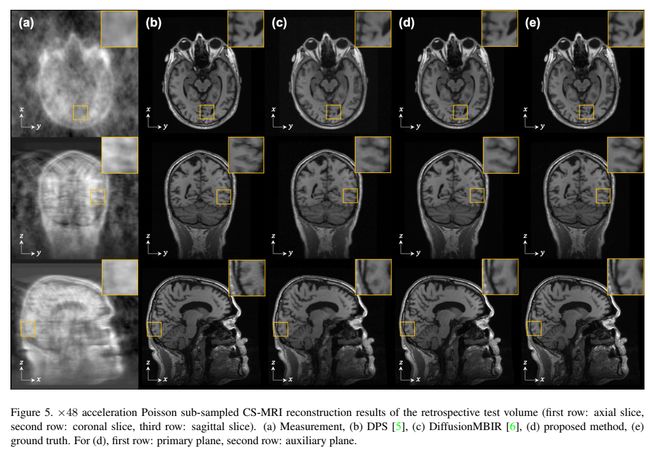
我们还通过对回顾性×48加速泊松子采样CSMRI体积进行重建来评估TPDM(图5，表2)。关于其他加速因素，请参见附录C.2。与MRZSR的结果相似，与现有技术2D/3D逆向问题解决方法相比，TPDM显示出最好的结果。图5还显示，TPDM能够准确地重建细节，优于其他所有方法。

5.3. 稀疏视图CT (SV-CT)

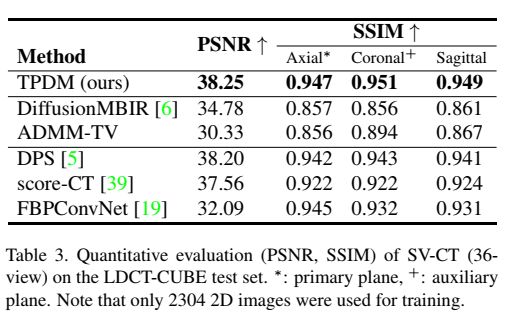
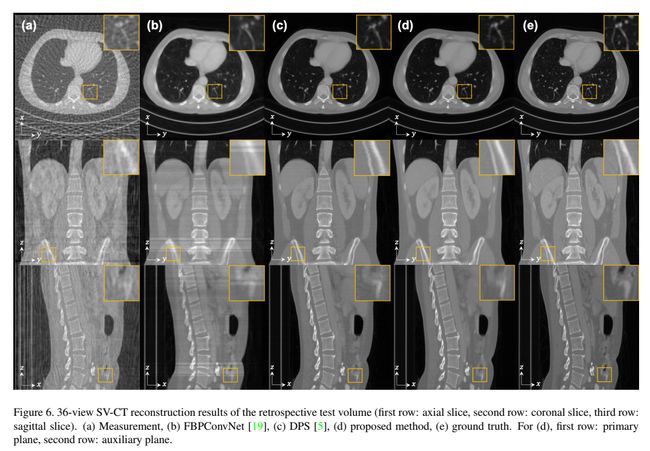
CT问题仅使用了9卷(约2000张2D图像)作为训练数据集数据来测试TPDM在极小数据条件下的性能。36视图SV-CT的实验结果见图6，表3。尽管使用高度有限的数据集进行训练，但TPDM模型与其他模型相比表现良好。虽然相对于DPS[5]的量化改进并不大，但TPDM的性能明显优于DPS，因为DPS是一个2D逆问题求解器，在应用于3D逆问题时，会在批处理方向引入伪影。在FBPConvNet[19]中，轴向的SSIM改进较小，但由于它也是2D模型，因此在其他切片方向上表现不佳。此外，在使用监督技术训练的卷积网络中常见的模糊结果仍然很明显。

5.4. 无条件3D体素体积生成

使用TPDM，我们尝试无条件地生成完整的3D体素体(算法见附录A .3)。我们使用BMR-ZSR-1mm数据集训练TPDM模型，并使用它生成人类头部的MRI体积，其结果如图7所示。值得注意的是，我们能够在不依赖任何测量指导的情况下，以高分辨率和高质量创建完整的三维体素体积。我们认为TPDM生成3D体积的能力不仅仅是由于DPS步骤中测量提供的2D图像顺序指导，还由于两种扩散模型的替代去噪算法。这里提出的经验证据支持我们提出的数据分布假设的合理性。

6. Conclusion

在这项研究中，我们引入了TPDM，一种通过预训练的两个垂直的二维扩散模型来解决一般的三维反问题并生成体素体积的方法。TPDM以完全无监督的方式工作，不需要对单个逆问题进行任何微调。它在处理三维体积时，不使用任何三维扩散模型，而是将三维分布假设为二维分布的乘积分布，在利用三维体积概率分布的同时，有效地避免了维数灾难。我们的研究结果表明，TPDM在几个医疗3D重建问题上优于现有的最先进的3D逆问题解决方法，即使在数据量非常有限的情况下也是如此。最后，利用TPDM和一种新颖的前向测量模型，我们首次尝试了基于扩散的z方向超分辨率MRI图像，并在技术和临床方面展示了卓越的结果。

Appendix

A. 附加算法

A.1. Training TPDM

A.2. Sampling with real value K

A.3. 3D voxel volume generation with TPDM

B. Dataset

B.1. BMR-ZSR-5mm

B.2. LDCT-CUBE

C. 其他结果

C.1. MRI z轴超分辨率(MR-ZSR)

C.2. 压缩感知MRI (CS-MRI)

D. 采样超参数

E. 计算资源

TPDM的训练和采样过程都是在两个NVIDIA GeForce RTX 3090 gpu上执行的。采用文中阐述的设置，MRI和CT模型的训练时间分别约为3天和1天，每个2D模型，无论是主模型还是辅助模型。根据具体问题类型，TPDM采样过程需要大约24至36小时的时间框架。采样时采用6个批处理大小，TPDM消耗的VRAM总计约为48GB。

F. 代码可用性