算法刷题 week3

1.重建二叉树

题目

题解

(递归) O(n)

递归建立整棵二叉树：先递归创建左右子树，然后创建根节点，并让指针指向两棵子树。

前序遍历（根 左 右）中序遍历（左 根 右） 后序遍历（左 右 根）

具体步骤如下：

1. 先利用前序遍历找根节点：前序遍历（根 左 右）的第一个数，就是根节点的值；
2. 在中序遍历中找到根节点的位置 k，则 k 左边是左子树的中序遍历（左 根 右），右边是右子树的中序遍历；
3. 假设左子树的中序遍历的长度是 l，则在前序遍历中，根节点后面的 l 个数，是左子树的前序遍历，剩下的数是右子树的前序遍历；
4. 有了左右子树的前序遍历和中序遍历，我们可以先递归创建出左右子树，然后再创建根节点；

时间复杂度分析

我们在初始化时，用哈希表(unordered_map)记录每个值在中序遍历中的位置，这样我们在递归到每个节点时，在中序遍历中查找根节点位置的操作，只需要 O(1) 的时间。此时，创建每个节点需要的时间是 O(1)，所以总时间复杂度是 O(n)。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
//preorder前序遍历（根 左 右），inorder中序遍历（左 根 右）
class Solution {
public:
    unordered_map<int, int> pos; 
    
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int n = preorder.size();
        for (int i = 0; i < n; ++i)
            pos[inorder[i]] = i;  //用哈希表记录每个值在中序遍历中的位置 
        return dfs(preorder, inorder, 0, n - 1, 0, n - 1);    
    }
    //前序遍历pre的范围是[pl,pr], 中序遍历in的范围是[il,ir]
    TreeNode* dfs(vector<int>& pre, vector<int>& in, int pl, int pr, int il, int ir) {
        if (pl > pr) return NULL;
        int k = pos[pre[pl]] - il;  //寻找前序的根节点在中序遍历中是在第几个位置
        TreeNode* root = new TreeNode(pre[pl]); //生成新的根节点
        root->left = dfs(pre, in, pl + 1, pl + k, il, il + k - 1);
        root->right = dfs(pre, in, pl + k + 1, pr, il + k + 1, ir);
        return root;
    }
};

2.二叉树的下一个节点

题目

题解

(模拟) O(h)

这道题目就是让我们求二叉树中给定节点的后继。

中序遍历（左 根 右）

分情况讨论即可，如下图所示：

1. （左 根 右）如果当前节点有右儿子，则右子树中最左侧的节点就是当前节点的后继。比如F的后继是H；
2. （左 根）如果当前节点没有右儿子，**则需要沿着father域一直向上找，找到第一个是其(这个其非当前节点)father左儿子的节点，该节点的father就是当前节点的后继。**比如当前节点是D，则第一个满足是其father左儿子的节点是F，则C的father就是D的后继，即F是D的后继。

时间复杂度分析

不论往上找还是往下找，总共遍历的节点数都不大于树的高度。所以时间复杂度是 O(h)，其中 h 是树的高度。

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode *father;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL), father(NULL) {}
 * };
 */
class Solution{
public:
	TreeNode* inorderSuccessor(TreeNode* p) {
        if (p->right) {
            p = p->right;  //易错带
            while (p->left) p = p->left;
            return p;
        }
        //p == p->father->right 用来判断p是否是右节点
        while (p->father && p == p->father->right) p = p->father;
        return p->father;
    }
};

3.用两个栈实现队列

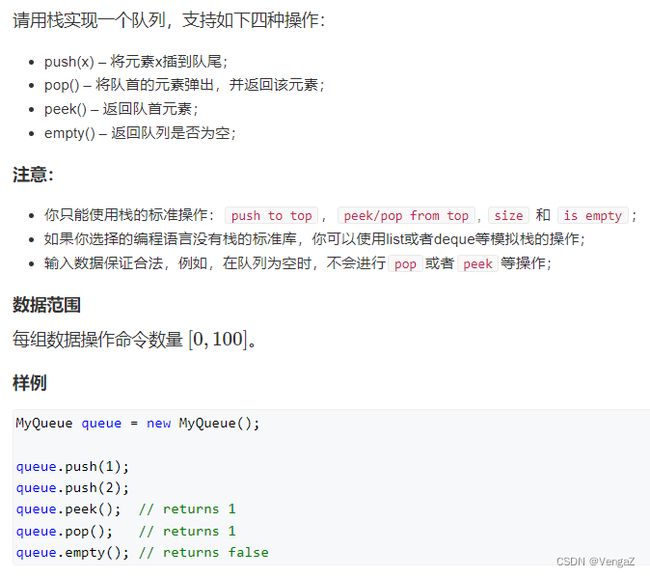
题目

题解

(栈，队列) O(n)

这是一道基础题，只要把功能实现对就可以，不需要考虑运行效率。

我们用两个栈来做，一个主栈，用来存储数据；一个辅助栈，用来当缓存。

栈：先进后出，队列：先进先出

• push(x)，我们直接将 x 插入主栈中即可。
• pop()，此时我们需要弹出最先进入栈的元素，也就是栈底元素。我们可以先将所有元素从主栈中弹出，压入辅助栈中。则辅助栈的栈顶元素就是我们要弹出的元素，将其弹出即可。然后再将辅助栈中的元素全部弹出，压入主栈中。
• peek()，可以用和pop()操作类似的方式，得到最先压入栈的元素。
• empty()，直接判断主栈是否为空即可。

时间复杂度分析

• push()：O(1)；
• pop(): 每次需要将主栈元素全部弹出，再压入，所以需要 O(n) 的时间；
• peek()：类似于pop()，需要 O(n) 的时间；
• empty()：O(1)；

class MyQueue {
public:
    /** Initialize your data structure here. */
    stack<int> stk, cache;
    
    MyQueue() {  //初始化，如果栈不为空，则用while()清空
        while (!stk.empty()) {
            stk.pop();
        }
        while (!cache.empty()) {
            cache.pop();
        }
    }
    
    /** Push element x to the back of queue. */
    void push(int x) {
        stk.push(x);
    }
    
    void copy(stack<int>& a, stack<int>& b) {
        while (a.size()) {
            b.push(a.top());
            a.pop();
        }
    }
    
    /** Removes the element from in front of queue and returns that element. */
    int pop() {
        if (stk.empty()) return -1;  //如果栈为空，返回-1
        copy(stk, cache);
        int res = cache.top();
        cache.pop();
        copy(cache, stk);
        return res;
    }
    
    /** Get the front element. */
    int peek() {
        if (stk.empty()) return NULL;  //如果栈为空，返回NULL
        copy(stk, cache);
        int res = cache.top();
        copy(cache, stk);
        return res;
    }
    
    /** Returns whether the queue is empty. */
    bool empty() {
        return stk.empty();
    }
};

/**
 * Your MyQueue object will be instantiated and called as such:
 * MyQueue obj = MyQueue();
 * obj.push(x);
 * int param_2 = obj.pop();
 * int param_3 = obj.peek();
 * bool param_4 = obj.empty();
 */