红黑树相关知识总结
一、问题引入
1、什么是红黑树?
2、红黑树的出现是为了解决什么问题?
3、红黑树的实现逻辑是来源于哪里?
4、红黑树的具体应用有哪些?
二、红黑树
1、红黑树的出现解决了二叉查找树维护困难的问题
1、红黑起源来自二叉查找树,那什么是二叉查找树呢?二叉查找树是一种高度平衡的二叉树,它也是树结构中最典型的数据结构,它既有数组的快速查找效率,也有链表快速插入和删除的特点。
2、二叉查找树的定义:二叉搜索树(Binary Search Tree),或者是一棵空树,或者是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值; 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值; 它的左、右子树也分别为二叉排序树。
从理论上来说,二叉查找树已经能够满足我们的要求的,因为他的时间复杂度为O(logn),这已经是效率很高的查找方法了,那为什么很多经典的工程中使用都是红黑树而不是二叉查找树呢?
3、我们来考虑这样一种情况,假如我们又一串数据,1 - 6,现在工程要求我们必须把数字1作为根节点,其他数字按照二叉查找树的要求依次插入,这时就会出现这样一种情况,因为2比节点大,因此2要作为1的右子树节点,3又比2大,因此3要作为节点2的右子树,依次类推,就会到得一个近似于链表的二叉查找树。
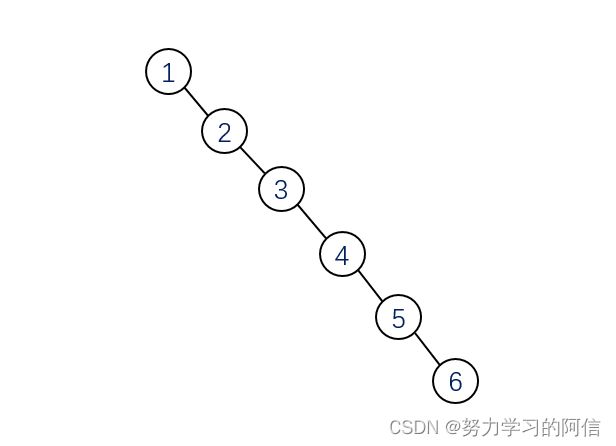
这样我们在插入、删除或者查找的时候,他的时间负责度就是O(n)了,这样就不满足二叉查找树的时间负责度了,所以为了解决掉这种问题,各位聪明的前辈们提出了红黑树这种特殊的数据结构。所谓的红黑树也就是将二叉查找树的定义放宽,这样既简化了平衡二叉树的维护难度也能满足我们工程的实际需求,多棒呀。
2、红黑树的性质
红黑树的性质总结就是五句话。
1、红黑树的节点不是红色就是黑色;
2、根节点是黑色的;
3、每个叶子节点都是黑色的;
4、如果一个节点是红色的,那么他的左右子树节点都是黑色的;
5、对每个节点来说,从该节点到期子孙节点的任意一条路径上都包含相同的黑色节点。
红黑树的性质就是这五点,其中我们在构建红黑树的时候所有的叶子节点都是隐藏的且不存储数据的,他的存在是为了方便我们对红黑树操作存在的。满足以上五点性质的二叉树就是红黑树。

这是我拿的零声教育的图(所有的叶子节点都是黑色且都隐藏),我们可以按照以上五条性质去判断上面那个才是红黑树。首先,所有的节点不是黑色就是红色都符合;4的根节点是红色的,不符合性质而要求,排除4;所有的叶子节点隐藏且颜色是黑色都满足,然后如果一个节点是红色的,那么他的儿子都是黑色的,都符合;然后是性质屋,图一的路径14-8 和 14-20-26黑色节点数不同, 排除;图3的14-8-叶子节点和14-20-26-叶子节点数量不相同,排除;2的所有路径包含黑色节点数量都是3,因此2就是一个红黑树。
红黑树的定义——代码实现
// 1、红黑树定义
typedef struct _rbTree_node {
struct _rbTree_node *left;
struct _rbTree_node *right;
// 性质中是没有parent的,这里定义parent是为了后面调整红黑树性质存在的
struct _rbTree_node *parent;
unsigned char color;
} rbTree_node;
typedef struct _rbTree {
KEY_TYPE key;
void *value;
rbTree_node *T;
rbTree_node *nil; // 空节点
} rbTree;
在这里是将红黑树的性质和key-value分开来的,其中,红黑树的节点都拥有指向孩儿子的左右指针,同时还有指向父亲节点的指针parent;RBTree定义了一个根节点和空节点,注意是空节点不是nullptr;他们的区别就是空节点拥有红黑树节点的所有性质,这样我们就可以借助空节点去实现某些操作,如果是nullptr空指针的话,程序访问到叶子节点的时候就会报错。
3、红黑树的左旋右旋
我们在这里要介绍红黑树的左旋和右旋,那为什么要介绍左旋和右旋的,左旋和右旋的出现是为了解决红黑树在插入新节点后红黑树的性质被破坏,为了去维护红黑树所提出的解决办法,总共有左旋、右旋和变色三种方法,这里我们仅介绍左旋和右旋。
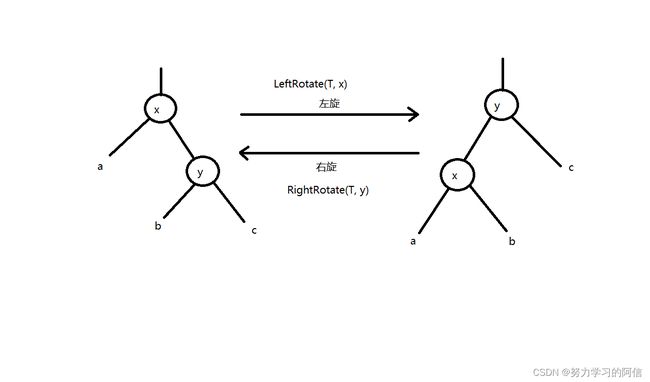
1、左旋
按照图片的内容,以节点X左旋步骤依次是节点X的父节点指向节点Y,节点X的右儿子节点指向节点Y的左儿子节点,节点Y的左儿子节点指向节点X。左旋总共改变了三个指针的指向,但在代码实现的时候我们需要改变六个指针的指向,这个后面再说。具体如如下图。

接下来看具体的左旋代码实现
void rbtree_left_rotate(rbtree *T, rbtree_node *x) {
rbtree_node *y = x->right;
x->right = y->left; //1 1
if (y->left != T->nil) { //1 2
y->left->parent = x;
}
y->parent = x->parent; //1 3
if (x->parent == T->nil) { //1 4
T->root = y;
} else if (x == x->parent->left) {
x->parent->left = y;
} else {
x->parent->right = y;
}
y->left = x; //1 5
x->parent = y; //1 6
}
我们来看代码,首先必须定义一个指针指向节点X的右儿子节点,这是因为我们第一个要改变的指针就是节点X的右指针指向,因此需要先记录该节点的情况,然后再去修改。
(1)首先将节点X的 right 指针指向节点Y的 left 指针;接下来判断节点Y是否是叶子节点,如果不是,将节点Y的左子树节点的 parent 指针指向节点X。

(2)这步将节点Y的 parent 指针指向节点X的 parent 指向的节点,此时需要判断节点X的 parent 指向的节点是否是叶子节点。如果节点X的父节点是叶子节点,此时红黑树的根节点就是节点Y。

(3)此时说明节点X的父节点不是叶子节点,此时节点X可能是节点X的父节点的左儿子节点或者右儿子节点,此时需要分别处理。如果节点X是其父节点的左子树节点,此时需要将节点X的父节点的 left 指针指向节点Y;如果是右子树节点,此时需要将节点X的父节点的 right 指针指向节点Y。最后一步就是将节点Y的 left 指针指向节点X,节点X的 parent 指向节点Y。到此,左旋完成。
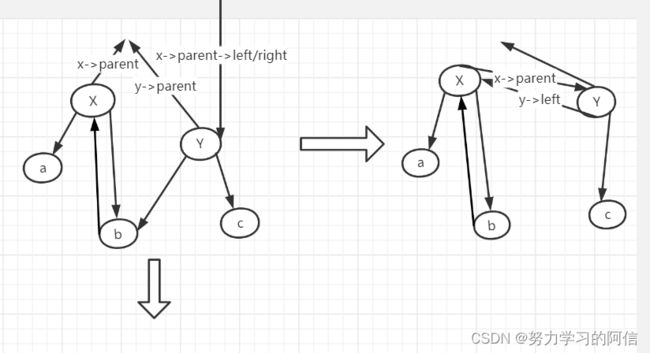
然后将得到的图稍作调整就得到左旋后的结果了

2、右旋
右旋和左旋想法很接近,只需要将X换成Y,left换成right即可,分析方法和上面一直,此处就不做多余赘述。
void rbtree_right_rotate(rbtree *T, rbtree_node *y) {
rbtree_node *x = y->left;
y->left = x->right;
if (x->right != T->nil) {
x->right->parent = y;
}
x->parent = y->parent;
if (y->parent == T->nil) {
T->root = x;
} else if (y == y->parent->right) {
y->parent->right = x;
} else {
y->parent->left = x;
}
x->right = y;
y->parent = x;
}
4、红黑树的节点插入
红黑树的插入比较难理解,我绝得先从最简单的开始。
(1)如果红黑树是空树,此时插入的节点就是根节点,此时需要修改节点颜色为黑色。
(2)插入节点的父节点是黑色。此时可以直接插入不用修改颜色。
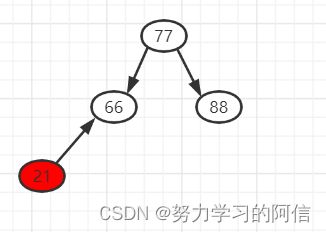
(3)插入节点的父节点是红色,叔父节点存在且为红色,此时在插入节点之前需要先将父节点、叔父节点颜色修改为黑色,然后在插入节点,具体过程如下图。

(4)父节点是红色,叔父节点不存在或者为黑色,当前节点和父亲节点均为左子节点。此时需要对节点66进行旋转,旋转后将节点3插入红黑树

(5)父节点是红色且是左子节点,叔父节点不存在或者为黑色,当前节点是右子节点。此时首先以节点21右旋,得到后的红黑树就是(4)所面临的那种,此时只要再执行(4)即可得到需要的红黑树。

(6)父节点是红色,叔父节点不存在或者是黑色,当前节点和父节点均为右子节点。首先将节点90变黑,节点90的父节点变红,然后在将节点88左旋即可。

(7)父节点是红色且为右子节点,叔父节点不存在或者为黑色,当前节点为左子节点。首先以节点90右旋,旋转后得到的红黑树和(6)一样,此时按照(6)去左旋节点88即可。

好了,说到这里红黑树的插入就完了,接下来直接看代码。
void rbtree_insert_fixup(rbtree *T, rbtree_node *z) {
while (z->parent->color == RED) { //z ---> RED
if (z->parent == z->parent->parent->left) {
rbtree_node *y = z->parent->parent->right;
if (y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
} else {
if (z == z->parent->right) {
z = z->parent;
rbtree_left_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_right_rotate(T, z->parent->parent);
}
}else {
rbtree_node *y = z->parent->parent->left;
if (y->color == RED) {
z->parent->color = BLACK;
y->color = BLACK;
z->parent->parent->color = RED;
z = z->parent->parent; //z --> RED
} else {
if (z == z->parent->left) {
z = z->parent;
rbtree_right_rotate(T, z);
}
z->parent->color = BLACK;
z->parent->parent->color = RED;
rbtree_left_rotate(T, z->parent->parent);
}
}
}
T->root->color = BLACK;
}
void rbtree_insert(rbtree *T, rbtree_node *z) {
rbtree_node *y = T->nil;
rbtree_node *x = T->root;
while (x != T->nil) {
y = x; // y指向x的parent节点,记录位置
if (z->key < x->key) {
x = x->left;
} else if (z->key > x->key) {
x = x->right;
} else { //Exist
return ;
}
}
z->parent = y;
if (y == T->nil) {
T->root = z;
} else if (z->key < y->key) {
y->left = z;
} else {
y->right = z;
}
z->left = T->nil;
z->right = T->nil;
z->color = RED;
rbtree_insert_fixup(T, z);
}
在插入的时候我们需要定义两个节点X和Y,然后我们看第一个while是干什么的,当我们去向红黑树插入节点的时候,插入的位置一定是最后一个几点,也就是叶子节点的父亲节点。那while循环结束后我们得到了 x = T->nil; 也就是说此时节点X指向红黑树的叶子节点,我们拿到他是没有任何用处的,我们需要的是叶子节点的父节点,因此我们在每次对节点X进行遍历之前, 先用节点Y去记录节点X的位置,这样,当节点X指向叶子节点的时候,节点Y指向叶子节点的父亲节点位置,这个位置就是我们需要插入的位置。
那叶子节点也是有 parent 指针的呀,那为什么不用叶子节点的 parent 指针去获取插入位置呢?这是因为叶子节点虽然有 parent 指针,但是叶子节点是空节点,他的 parent 指针是没有指向的,因此这种方法不行的。
接下来,我们就可以将节点Z的 parent 指针指向节点Y,此时还需要判断节点Y是否是叶子节点,如果是,那么插入的节点Z就是红黑树的根节点。然后我们根据节点Z 的key值大小去选择节点Y的左右子树,也就是将节点Y的 left/right 指针指向节点Z。最后将节点Z的 left、right 指针指向叶子节点,节点Z的颜色置为红色即可。
此时红黑树就完成插入了,插入的节点很多概率会破坏红黑树的性质4,这时我们需要调整它去满足红黑树的性质4。具体实现参考上面的分析和rbTree_insert_fixup函数即可。