图解LeetCode15:三数之和(排序+双指针方法)
LeetCode15:三数之和
给你一个包含n个整数的数组nums,判断nums中是否存在三个元素a,b,c,使得a+b+c=0?请你找出所有和为0且不重复的三元组
注意:
答案中不可以包含重复的三元组
示例:
输入:nums = [-1, 0, 1, 2, -1, -4]
输出:[[-1, -1, 2], [-1, 0, 1]]
输入:nums = []
输出:nums = []
输入:nums = [0]
输出:[]
提示:
0 <= nums.length <= 3000
-10^5 <= nums[i] <= 10^5
思路:
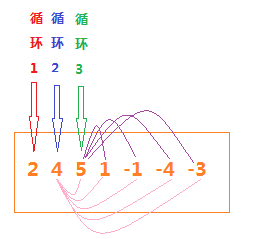
这种情况最直接想到的就是递归求解,使用三重循环,逐渐相加,找到和为零的时候,就添加到数组中
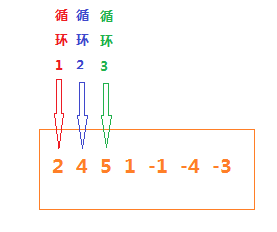
这种方法虽然可以解决该题,得到答案,但是存在两个问题
①、因为使用了三个循环,所以时间复杂度为O(n^3)
②、这种方法会把所有的结果都输出一次,结果中会有重复,比如一个数组[0,0,0,0,0],输出结果就会[[0,0,0], [0,0,0], [0,0,0]]
所以就要选择一种方案,优化这种思路,使得时间复杂度和结果重复的问题都要解决。
解法
可以选择排序+双指针的方法
排序+双指针
①首先将给出的数组排序,按照从高到低,这样一来,对于一串数字,前后数字相加为0的概率会更大,就可以采用前后同时遍历的方法
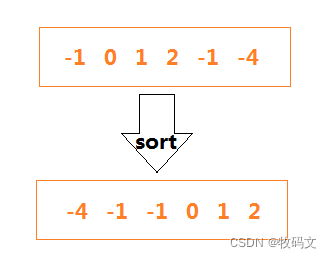
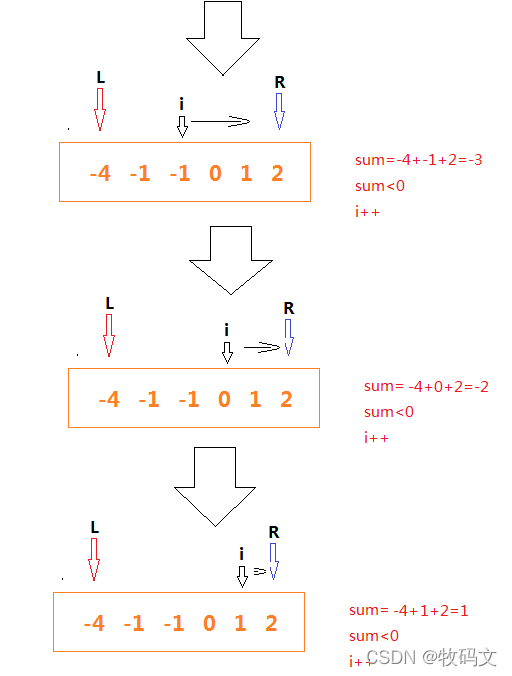
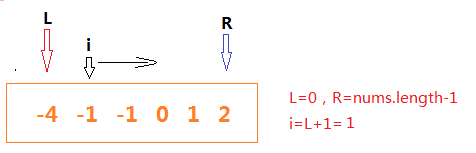
②使用两个指针,一个初始在列表开头,另一个初始在列表结尾,然后遍历中间数字相加
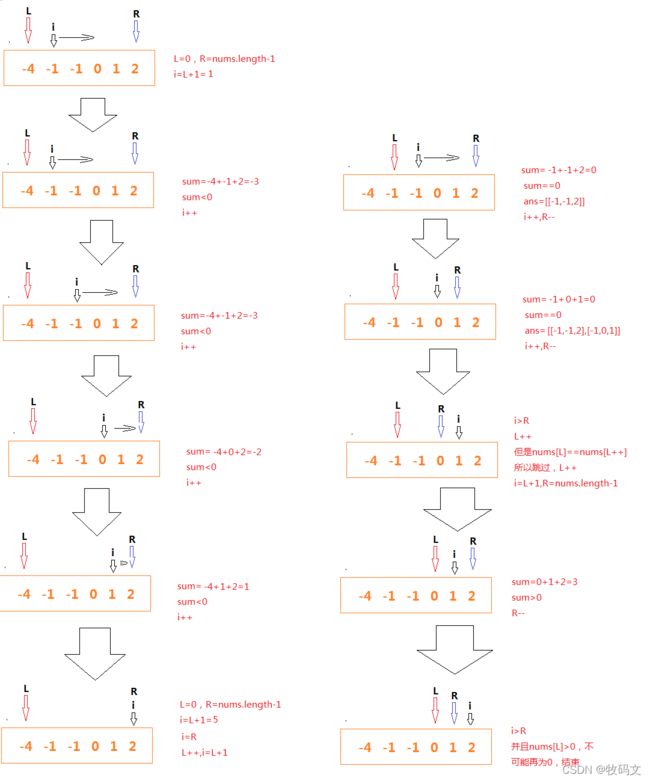
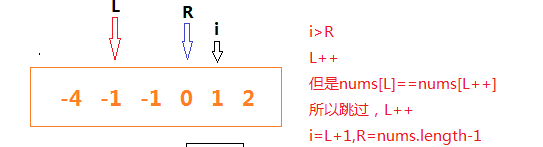
⑤当三数之和等于零,判断前后数字是否相同,相同说明为重复,需要跳过
⑥当开头指针不小于结尾指针时,并且首指针数值为正数,循环结束
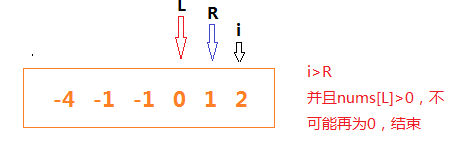
代码
public List<List<Integer>> threeSum(int[] nums){
// 结果为一个数组
List<List<Integer>> res = new ArrayList();
int len = nums.length;
if(nums == null || len < 3) return ans;
// 列表排序
Arrays.sort(nums);
// 开始遍历
for(int L = 0; L < len; L++){
// 如果全是正数,则结果一定不会是0
if(nums[L] > 0) break;
// 如果重复,就跳过
if(L > 0 && nums[L] == nums[L-1]) continue;
// 定义i和R
int i = L + 1, R = len - 1;
// 开始移动指针求解
while(i < R){
int sum = nums[L] + nums[i] + nums[R];
if(sum == 0){
// 加入ans结果
res.add(Arrays.asList(nums[L], nums[i], nums[R]));
// 判断是否数值有相同
while(i < R && nums[i] == nums[i + 1]) i++;
while(i < R && nums[R] == nums[R - 1]) R--;
}
// 如果小于零,就右移动
else if(sum < 0) i++;
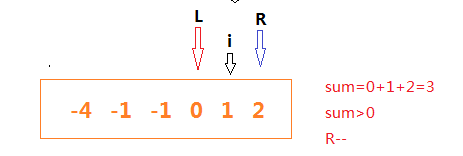
// 如果大于零,就R移动
else if(sun > 0) R--;
}
}
// 返回结果
return res;
}
测试
public static void main(String[] args){
LeetCode15 lc = new LeetCode15();
Sysout.out.println(lc.threeSum({-1, 0, 1, 2, -1, -4}))
}
结果
[[-1, -1, 2], [-1, 0, 1]]
神奇的排序加双指针,这一方式简直堪称神奇,可以代替许多暴力递归的方法,要多加注意才是