图----无向图、有向图
1.无向图定义
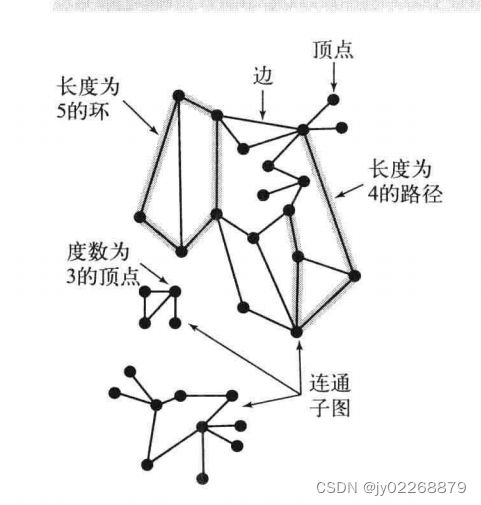
图的定义:图是由一组顶点和一组能够将两个顶点相连的边组成
边:edge
顶点:vertex
连通图:如果从任意一个顶点都存在一条路径到达另外一个任意顶点,我们称这幅图是连通图。
非连通图:由若干连通的部分组成,他们都是其极大连通子图。
自环:即一条连接一个顶点和其自身的边
平行边:连接同一顶点的两条边称为平行边
图的密度:是指已经连接的顶点对占所有可能被连接的顶点对的比例。在稀疏图中,被连接的顶点对很少;而在稠密图中,只有少部分顶点对之间没有边连接。
二分图:是一种能够将所有结点分为两部分的图,其中图的每条边所连接的两个顶点都分别属于不同的部分。
2.图的不同表示方法
2.1邻接表数组表示
用一个以顶点为索引的列表数组,其中的每个元素都是和该顶点相邻的定点列表
2.2邻接矩阵 表示
用一个V乘以V的布尔矩阵。当顶点V和顶点W之间有相连的边时,定义V行W列的元素值为true,否则为false。如果含有上百万个顶点,V的平方个布尔值所需要的空间会非常大。
3.相关API及代码
package com.sid.graph;
public class Vertex {
String value;//顶点的值
Edge firstEdge;//第一条边
int index;//在外层数组的下标
public Vertex(String value, Edge firstEdge,int index) {
super();
this.value = value;
this.firstEdge = firstEdge;
this.index = index;
}
}
package com.sid.graph;
public class Edge {
Vertex vertex;//该边对应的顶点
int weight;//权重,无向图,有向图权重为0
Edge next;//下一个边
/**
* 构建一条边 weight未0表示无向图或者有向图 不为0表示网
* @param vertex
* @param weight
* @param next
*/
public Edge(Vertex vertex, int weight, Edge next) {
super();
this.vertex = vertex;
this.weight = weight;
this.next = next;
}
}
package com.sid.graph;
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
public class Graph {
/**
* 顶点数
*/
private final int V;
/**
* 边数
*/
private int E;
/**
* 邻接表
*/
private List adj;
public Graph(int V) {
this.V = V;
this.E = 0;
adj = new ArrayList(V); /** 创建邻接表 */
}
public int V() {
return V;
}
public int E() {
return E;
}
/**
* 插入顶点
*/
public Vertex addVertex(String value) {
int size = adj.size();
Vertex vertex = new Vertex(value, null,size);
adj.add(vertex);
return vertex;
}
/**
* 获取顶点
*/
public Vertex getVertexByValue(String value) {
for (int i = 0; i < V; i++) {
if (adj.get(i).value.equals(value)) {
return adj.get(i);
}
}
return null;
}
/**
* 获取顶点
*/
public Vertex getVertexByIndex(int index) {
return adj.get(index);
}
/**
* 添加无向图的边
* @param vertex1 第一个顶点
* @param vertex2 第二个顶点
*/
public void addUndigraphEdge(Vertex vertex1,Vertex vertex2) {
//因为是无向图,所以就直接加入
addEdgeByVertex(vertex1,vertex2,0);
addEdgeByVertex(vertex2,vertex1,0);
}
/**
* 添加有向图的边
* @param start 开始节点
* @param end 结束节点
*/
public void addDigraphEdge(Vertex start,Vertex end) {
//因为是有向图,所以只有一条边
addEdgeByVertex(start,end,0);
}
/**
* 添加一条由start-->end的边
*
* @param start
* @param end
* @param weight 权重未0表示无向图或者有向图,部位0表示网
*/
private void addEdgeByVertex(Vertex start, Vertex end, int weight) {
//1、找到第一个顶点
Vertex v1 = this.getVertexByValue(start.value);
if(v1 == null){
v1 = addVertex(start.value);
}
//2、检查这条边是否已经存在,已经存在就直接报错
for (Vertex w : adj(v1)) {
if (end.value.equals(w.value)) {
System.out.println("边" + start.value + "-->" + end.value + "已经加入,不可以再加入");
return;
}
}
//3.添加
Edge firstEdge = v1.firstEdge;
if (firstEdge == null) {
firstEdge = new Edge(end, weight, null);
v1.firstEdge = firstEdge;
} else {
//当前节点变为第一个节点
Edge nowEdge = new Edge(end, weight, null);
v1.firstEdge = nowEdge;
nowEdge.next = firstEdge;
}
E++;
}
/**
* 计算V节点的度数
*/
public static int degree(Graph g, int v) {
int degree = 0;
Edge firstEdge = g.getVertexByIndex(v).firstEdge;
while (firstEdge != null) {
degree++;
firstEdge = firstEdge.next;
}
return degree;
}
/**
* 计算所有顶点的最大度数
*/
public static int maxDegree(Graph G) {
int max = 0;
for (int v = 0; v < G.V(); v++) {
if (degree(G, v) > max) {
max = degree(G, v);
}
}
return max;
}
/**
* 计算所有顶点的平均度数
*/
public static int avgDegree(Graph G) {
return 2 * G.E() / G.V();
}
/**
* 计算自环的的个数
*/
public static int numberOfSelfLoops(Graph g) {
int count = 0;
for (int v = 0; v < g.V(); v++) {
for(int w : g.adj(v)){
if(v == w){
count++;
}
}
}
return count / 2; //每条边都被记过两次
}
/**
* 得到跟V节点相邻的所有节点
*/
public static List adj(Vertex vertex) {
List result = new LinkedList();
Edge firstEdge = vertex.firstEdge;
while (firstEdge != null) {
result.add(firstEdge.vertex);
firstEdge = firstEdge.next;
}
return result;
}
/**
* 得到跟V节点相邻的所有节点下标 入参是节点的数组下标
*/
public List adj(int index) {
List result = new ArrayList();
Edge firstEdge = this.getVertexByIndex(index).firstEdge;
while (firstEdge != null) {
result.add(firstEdge.vertex.index);
firstEdge = firstEdge.next;
}
return result;
}
/**
* 图的邻接表的字符串表示
*/
public String toString() {
String s = V + " vertices, " + E + " edges\n";
for (int v = 0; v < V; v++) {
Vertex vertex = this.getVertexByIndex(v);
s += vertex.value + ": ";
for (Vertex w : adj(vertex)) {
s += w.value + "";
}
s += "\n";
}
return s;
}
}
4.深度优先搜索
4.1 找到以起点s连通的所有顶点,和个数
实现:
用一个递归方法来遍历所有顶点,在访问一个顶点时:
将它标记为已访问
递归地访问它的所有没有被标记过的邻居顶点
package com.sid.graph;
public class DepthFirstSearch {
private boolean[] marked;
private int count;
public DepthFirstSearch(Graph G,int s){
marked = new boolean[G.V()];
dfs(G,s);
}
private void dfs(Graph G, int index) {
marked[index] = true;
count++;
for(int w : G.adj(index)){
if(!marked[w]){
dfs(G,w);
}
}
}
public boolean marked(int w ){
return marked[w];
}
public int count(){
return count;
}
}
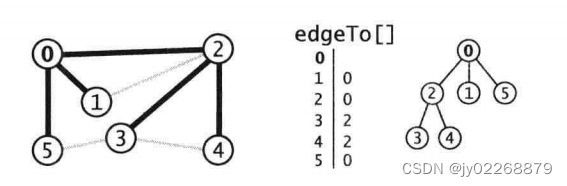
4.2深度优先搜索查找图中路径
注意这不一定是最短路径,比如说下面这个例子,查出来的0到1的路径,不是0----1,而是0----2----1
package com.sid.graph;
import java.util.Stack;
public class DepthFirstPaths {
private boolean[] marked; //这个顶点上调用过dfs()了吗
private int[] edgeTo; //从起点到一个顶点的已知路径上的最后一个顶点 比如S---A---C 则 edgeTo[C]=A edgeTo[C]其实表示的是谁直接指向C点
private final int s; //起点
public DepthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
dfs(G, s);
}
private void dfs(Graph G, int index) {
marked[index] = true;
for (int w : G.adj(index)) {
if (!marked[w]) {
edgeTo[w] = index;
dfs(G, w);
}
}
}
public boolean hasPathTo(int v){ //起点S是否有路径到V
return marked[v];
}
public Iterable pathTo(int v){
if(!hasPathTo(v)){
return null;
}
Stack path = new Stack();
for(int x = v ; x != s ; x = edgeTo[x]){
path.push(x);
}
path.push(s);
return path;
}
}
5.广度优先搜索
深度优先搜索得到的路径不仅取决于图的结构,还取决于图的表示和递归调用的性质。
“从S到给定目标的顶点V是否存在一条路径?如果有,找出其中最短的那条”,则需要用广度优先搜索。
实现:
1.使用一个队列来保存所有已经被标记过,但其邻接表还未被检查过的顶点
2.先将起点加入队列,然后重复以下步骤直到队列为空
取队列中的下一个顶点v并标记它
将与v相邻的所有未被标记过的顶点加入队列
package com.sid.graph;
import java.util.*;
public class BreadthFirstPaths {
private boolean[] marked; //这个顶点上调用过dfs()了吗
private int[] edgeTo; //从起点到一个顶点的已知路径上的最后一个顶点 比如S---A---C 则 edgeTo[C]=A edgeTo[C]其实表示的是谁直接指向C点
private final int s; //起点
public BreadthFirstPaths(Graph G, int s) {
marked = new boolean[G.V()];
edgeTo = new int[G.V()];
this.s = s;
bfs(G, s);
}
private void bfs(Graph G, int s) {
Queue queue = new PriorityQueue<>();
marked[s] = true;
queue.add(s);
while (!queue.isEmpty()){
int v = queue.poll();
for(int w : G.adj(v)){
if(!marked[w]){
edgeTo[w] = v;
marked[w] = true;
queue.add(w);
}
}
}
}
public boolean hasPathTo(int v){
return marked[v];
}
public Iterable pathTo(int v){
if(!hasPathTo(v)){
return null;
}
Stack path = new Stack();
for(int x = v ; x != s ; x = edgeTo[x]){
path.push(x);
}
path.push(s);
return path;
}
}
6.连通分量
无向图G的极大连通子图称为G的连通分量( Connected Component)。
任何连通图的连通分量只有一个,即是其自身,非连通的无向图有多个连通分量。
实现
使用marked[]数组来寻找一个顶点作为每个连通分量中深度优先搜索的起点。
递归的深度优先搜索第一次调用的参数是顶点0,它会标记所有与0连通的顶点。
然后构造函数中for循环会查找每个没有被标记的顶点,并且递归调用dfs()来标记和它相邻的所有顶点。
使用一个以顶点作为索引的数组id[],将同一个连通分量的顶点和连通分量的标识符关联起来(int 值)。这个数组是的connected()方法的实现变得十分简单。
标识符0会被赋予第一个连通分量中的所有顶点,1会被赋予第二个连通分量中的所有顶点,以此类推。这样所有的标识符都会如API中指定的那样在0到count()-1之间。这个约定使得以子图作为索引的数组成为可能。
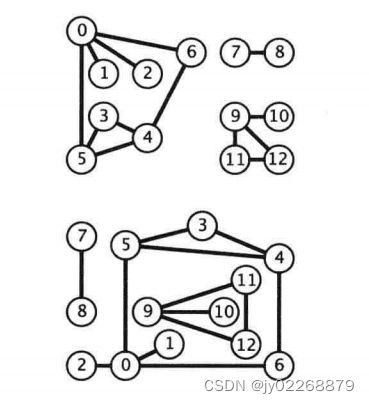
例子
最后
id[0]= 0
id[1]= 0
id[2]= 0
id[3]= 0
id[4]= 0
id[5]= 0
id[6]= 0
id[7]= 1
id[8]= 1
id[9]= 2
id[10]= 2
id[11]= 2
id[12]= 2
也就是说count[]的值相同的是一个连通分量,count[]的值不同的节点之间是走不通的。
代码
package com.sid.graph;
public class CC {
private boolean[] marked;
private int[] id;
private int count;
public CC(Graph G){
marked = new boolean[G.V()];
id = new int[G.V()];
for(int s = 0 ; s < G.V(); s++){
if(!marked[s]){
dfs(G,s);
count++;
}
}
}
private void dfs(Graph G,int v){
marked[v] = true;
id[v] = count;
for(int w : G.adj(v)){
if(!marked[w]){
dfs(G,w);
}
}
}
public boolean connected(int v, int w){
return id[v] == id[w];
}
public int id(int v){
return id[v];
}
public int count(){
return count;
}
}
7.G是无环图吗
使用深度优先处理
如果不存在自环和平行边,就是无环图
package com.sid.graph;
public class Cycle {
private boolean[] marked;
private boolean hasCycle;
public Cycle(Graph G){
marked = new boolean[G.V()];
for(int s = 0 ; s < G.V(); s++){
if(!marked[s]){
dfs(G,s,s);
}
}
}
private void dfs(Graph G, int v , int u){
marked[v] = true;
for(int w : G.adj(v)){
if(!marked[w]){
dfs(G,w,v);
}
else if(w != u){ //A---B 与B相邻的节点肯定有A,我理解的是无向图中他们属于同一条边,不是环。
hasCycle = true;
}
}
}
public boolean hasCycle(){
return hasCycle;
}
}
8.G是二分图吗(双色问题)
package com.sid.graph;
public class TwoColor {
private boolean[] marked;
private boolean[] color;
private boolean isTowColorable = true;
public TwoColor(Graph G){
marked = new boolean[G.V()];
color = new boolean[G.V()];
for(int s = 0 ; s < G.V(); s++){
if(!marked[s]){
dfs(G,s);
}
}
}
private void dfs(Graph G, int v) {
marked[v] = true;
for (int w : G.adj(v)){
if(!marked[w]){
color[w] = !color[v];
}else if(color[w] == color[v]){
isTowColorable = false;
return;
}
}
}
public boolean isBipartite(){
return isTowColorable;
}
}
9.符号图
节点里面装的不是数字,而是其他的,比如字符串
10.有向图定义
一副有方向性的图(或有向图)是由一组顶点和一组有方向的边组成的,每条有方向的边都连接着有序的一对顶点。
在一副有向图中,有向路径由一系列顶点组成,对于其中的每个顶点都存在一条有向边从它指向序列中的下一个顶点。
有向环为一条至少含有一条边且起点和终点相同的有向路径。
简单有向环是一条(除了起点和终点必须相同之外)不含有重复的顶点和边的环。
路径或者环的长度即为其中所包含的边数。
常见API
其他的方法在无向图里面写了。有向图添加边,也在无向图的添加边代码里面写了。唯一没写的是reverse方法。
reverse方法:
11.有向图的可达性
深度优先搜索的实现可以是的用例能够判断从给定的一个或者一组顶点能到达哪些其他顶点
package com.sid.graph;
public class DirectedDFS {
private boolean[] marked;
public DirectedDFS(Digraph G, Vertex v){
marked = new boolean[G.V()];
dfs(G,v);
}
public DirectedDFS(Digraph G, Iterable sources){
marked = new boolean[G.V()];
for(Vertex s : sources){
if(!marked[s.index] ){
dfs(G,s);
}
}
}
private void dfs(Digraph G, Vertex v){
marked[v.index] = true;
for(Vertex w : G.adj(v)){
if(!marked[w.index] ){
dfs(G,w);
}
}
}
public boolean marked(Vertex v){
return marked[v.index];
}
}
多点可达性的实际应用课在内存管理系统中,包括jvm的标记-清除垃圾回收算法。
有向图的寻找路径,跟无向图类似。