《动手学深度学习 Pytorch版》 7.1 深度卷积神经网络(LeNet)
7.1.1 学习表征
深度卷积神经网络的突破出现在2012年。突破可归因于以下两个关键因素:
- 缺少的成分:数据
数据集紧缺的情况在 2010 年前后兴起的大数据浪潮中得到改善。ImageNet 挑战赛中,ImageNet数据集由斯坦福大学教授李飞飞小组的研究人员开发,利用谷歌图像搜索对分类图片进行预筛选,并利用亚马逊众包标注每张图片的类别。这种数据规模是前所未有的。 - 缺少的成分:硬件
2012年,Alex Krizhevsky和Ilya Sutskever使用两个显存为3GB的NVIDIA GTX580 GPU实现了快速卷积运算,推动了深度学习热潮。
7.1.2 AlexNet
2012年横空出世的 AlexNet 首次证明了学习到的特征可以超越手动设计的特征。
AlexNet 和 LeNet 的架构非常相似(此书对模型稍微精简了一下,取出来需要两个小GPU同时运算的设计特点):
| 全连接层(1000) |
|---|
↑ \uparrow ↑
| 全连接层(4096) |
|---|
↑ \uparrow ↑
| 全连接层(4096) |
|---|
↑ \uparrow ↑
| 3 × 3 3\times3 3×3最大汇聚层,步幅2 |
|---|
↑ \uparrow ↑
| 3 × 3 3\times3 3×3卷积层(384),填充1 |
|---|
↑ \uparrow ↑
| 3 × 3 3\times3 3×3卷积层(384),填充1 |
|---|
↑ \uparrow ↑
| 3 × 3 3\times3 3×3卷积层(384),填充1 |
|---|
↑ \uparrow ↑
| 3 × 3 3\times3 3×3最大汇聚层,步幅2 |
|---|
↑ \uparrow ↑
| 5 × 5 5\times5 5×5卷积层(256),填充2 |
|---|
↑ \uparrow ↑
| 3 × 3 3\times3 3×3最大汇聚层,步幅2 |
|---|
↑ \uparrow ↑
| 11 × 11 11\times11 11×11卷积层(96),步幅4 |
|---|
↑ \uparrow ↑
| 输入图像( 3 × 224 × 224 3\times224\times224 3×224×224) |
|---|
AlexNet 和 LeNet 的差异:
- AlexNet 比 LeNet 深的多
- AlexNet 使用 ReLU 而非 sigmoid 作为激活函数
以下为 AlexNet 的细节。
-
模型设计
由于 ImageNet 中的图像大多较大,因此第一层采用了 11 × 11 11\times11 11×11 的超大卷积核。后续再一步一步缩减到 3 × 3 3\times3 3×3。而且 AlexNet 的卷积通道数是 LeNet 的十倍。
最后两个巨大的全连接层分别各有4096个输出,近 1G 的模型参数。因早期 GPU 显存有限,原始的 AlexNet 采取了双数据流设计。
-
激活函数
ReLU 激活函数是训练模型更加容易。它在正区间的梯度总为1,而 sigmoid 函数可能在正区间内得到几乎为 0 的梯度。
-
容量控制和预处理
AlexNet 通过暂退法控制全连接层的复杂度。此外,为了扩充数据,AlexNet 在训练时增加了大量的图像增强数据(如翻转、裁切和变色),这也使得模型更健壮,并减少了过拟合。
import torch
from torch import nn
from d2l import torch as d2l
net = nn.Sequential(
# 这里使用一个11*11的更大窗口来捕捉对象。
# 同时,步幅为4,以减少输出的高度和宽度。
# 另外,输出通道的数目远大于LeNet
nn.Conv2d(1, 96, kernel_size=11, stride=4, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 减小卷积窗口,使用填充为2来使得输入与输出的高和宽一致,且增大输出通道数
nn.Conv2d(96, 256, kernel_size=5, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
# 使用三个连续的卷积层和较小的卷积窗口。
# 除了最后的卷积层,输出通道的数量进一步增加。
# 在前两个卷积层之后,汇聚层不用于减少输入的高度和宽度
nn.Conv2d(256, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 384, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(384, 256, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
# 这里,全连接层的输出数量是LeNet中的好几倍。使用dropout层来减轻过拟合
nn.Linear(6400, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
nn.Linear(4096, 4096), nn.ReLU(),
nn.Dropout(p=0.5),
# 最后是输出层。由于这里使用Fashion-MNIST,所以用类别数为10,而非论文中的1000
nn.Linear(4096, 10))
X = torch.randn(1, 1, 224, 224)
for layer in net:
X=layer(X)
print(layer.__class__.__name__,'output shape:\t',X.shape)
Conv2d output shape: torch.Size([1, 96, 54, 54])
ReLU output shape: torch.Size([1, 96, 54, 54])
MaxPool2d output shape: torch.Size([1, 96, 26, 26])
Conv2d output shape: torch.Size([1, 256, 26, 26])
ReLU output shape: torch.Size([1, 256, 26, 26])
MaxPool2d output shape: torch.Size([1, 256, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 384, 12, 12])
ReLU output shape: torch.Size([1, 384, 12, 12])
Conv2d output shape: torch.Size([1, 256, 12, 12])
ReLU output shape: torch.Size([1, 256, 12, 12])
MaxPool2d output shape: torch.Size([1, 256, 5, 5])
Flatten output shape: torch.Size([1, 6400])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 4096])
ReLU output shape: torch.Size([1, 4096])
Dropout output shape: torch.Size([1, 4096])
Linear output shape: torch.Size([1, 10])
7.1.3 读取数据集
如果真用 ImageNet 训练,即使是现在的 GPU 也需要数小时或数天的时间。在此仅作演示,仍使用 Fashion-MNIST 数据集,故在此需要解决图像分辨率的问题。
batch_size = 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
7.1.4 训练 AlexNet
lr, num_epochs = 0.01, 10
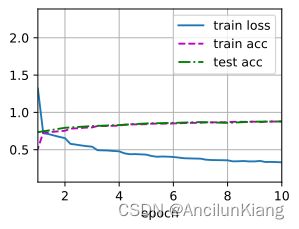
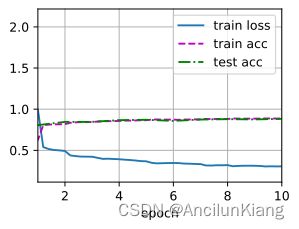
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu()) # 大约需要二十分钟,慎跑
loss 0.330, train acc 0.879, test acc 0.878
592.4 examples/sec on cuda:0
练习
(1)尝试增加轮数。对比 LeNet 的结果有什么不同?为什么?
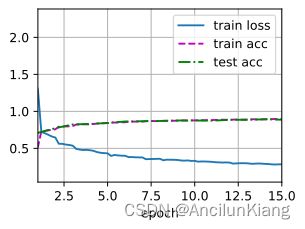
lr, num_epochs = 0.01, 15
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu()) # 大约需要三十分钟,慎跑
loss 0.284, train acc 0.896, test acc 0.887
589.3 examples/sec on cuda:0
相较于 LeNet 的增加轮次反而导致精度下降,AlexNet 具有更好的抗过拟合能力,增加轮次精度就会上升。
(2) AlexNet 模型对 Fashion-MNIST 可能太复杂了。
a. 尝试简化模型以加快训练速度,同时确保准确性不会显著下降。
b. 设计一个更好的模型,可以直接在 $28\times28$ 像素的图像上工作。
net_Better = nn.Sequential(
nn.Conv2d(1, 64, kernel_size=5, stride=2, padding=2), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=1),
nn.Conv2d(64, 128, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(128, 128, kernel_size=3, padding=1), nn.ReLU(),
nn.Conv2d(128, 64, kernel_size=3, padding=1), nn.ReLU(),
nn.MaxPool2d(kernel_size=3, stride=2),
nn.Flatten(),
nn.Linear(64 * 5 * 5, 1024), nn.ReLU(),
nn.Dropout(p=0.3),
nn.Linear(1024, 512), nn.ReLU(),
nn.Dropout(p=0.3),
nn.Linear(512, 10)
)
X = torch.randn(1, 1, 28, 28)
for layer in net_Better:
X=layer(X)
print(layer.__class__.__name__,'output shape:\t',X.shape)
Conv2d output shape: torch.Size([1, 64, 14, 14])
ReLU output shape: torch.Size([1, 64, 14, 14])
MaxPool2d output shape: torch.Size([1, 64, 12, 12])
Conv2d output shape: torch.Size([1, 128, 12, 12])
ReLU output shape: torch.Size([1, 128, 12, 12])
Conv2d output shape: torch.Size([1, 128, 12, 12])
ReLU output shape: torch.Size([1, 128, 12, 12])
Conv2d output shape: torch.Size([1, 64, 12, 12])
ReLU output shape: torch.Size([1, 64, 12, 12])
MaxPool2d output shape: torch.Size([1, 64, 5, 5])
Flatten output shape: torch.Size([1, 1600])
Linear output shape: torch.Size([1, 1024])
ReLU output shape: torch.Size([1, 1024])
Dropout output shape: torch.Size([1, 1024])
Linear output shape: torch.Size([1, 512])
ReLU output shape: torch.Size([1, 512])
Dropout output shape: torch.Size([1, 512])
Linear output shape: torch.Size([1, 10])
batch_size = 128
train_iter28, test_iter28 = d2l.load_data_fashion_mnist(batch_size=batch_size)
lr, num_epochs = 0.01, 10
d2l.train_ch6(net_Better, train_iter28, test_iter28, num_epochs, lr, d2l.try_gpu()) # 快多了
loss 0.429, train acc 0.841, test acc 0.843
6650.9 examples/sec on cuda:0
(3)修改批量大小,并观察模型精度和GPU显存变化。
batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
lr, num_epochs = 0.01, 10
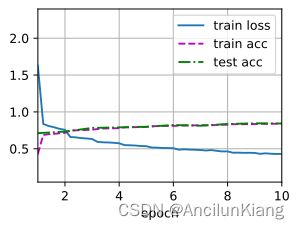
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu()) # 大约需要二十分钟,慎跑
loss 0.407, train acc 0.850, test acc 0.855
587.8 examples/sec on cuda:0
4G 显存基本拉满,精度略微下降,过拟合貌似严重了。
(4)分析 AlexNet 的计算性能。
a. 在 AlexNet 中主要是哪一部分占用显存?
b. 在AlexNet中主要是哪部分需要更多的计算?
c. 计算结果时显存带宽如何?
a. 第一个全连接层占用显存最多
b. 倒数第二个卷积层需要更多的计算
(5)将dropout和ReLU应用于LeNet-5,效果有提升吗?再试试预处理会怎么样?
net_try = nn.Sequential(
nn.Conv2d(1, 6, kernel_size=5, padding=2), nn.ReLU(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Conv2d(6, 16, kernel_size=5), nn.ReLU(),
nn.AvgPool2d(kernel_size=2, stride=2),
nn.Flatten(),
nn.Linear(16 * 5 * 5, 120), nn.ReLU(),
nn.Dropout(p=0.2),
nn.Linear(120, 84), nn.ReLU(),
nn.Dropout(p=0.2),
nn.Linear(84, 10))
lr, num_epochs = 0.6, 10
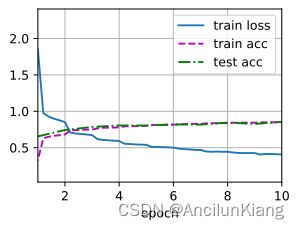
d2l.train_ch6(net_try, train_iter28, test_iter28, num_epochs, lr, d2l.try_gpu()) # 浅调一下还挺好
loss 0.306, train acc 0.887, test acc 0.883
26121.2 examples/sec on cuda:0
浅浅调一下,效果挺好,精度有所提升。