美赛整理之带参数的常微分方程拟合问题研究
带参数的常微分方程拟合问题研究
-
- 一.问题的背景:
- 二.提出一个较为简单,但是很有代表性的一个问题:
- 三.求解的基本原理:
- 四.求解的基本算法:
-
- 1.利用 m a t l a b matlab matlab遗传算法求解出其最优误差函数值:
- 2.差分后用 L I N G O LINGO LINGO求解:
一.问题的背景:
一般我们平常学习到的拟合问题大部分都是已知了函数表达式后,对于函数表达式里的系数进行的拟合问题。大部分的教材上其实并没有见讲解该如何对不能求解出相关表达式的函数关系的参数拟合求解。而且LINGO也是没有现成的微分符号表达2阶微分。因此,我通过在网上查阅部分资料提出了自己的一些小想法,用来求解一般的较为复杂的微分方程拟合的问题,并且使得解有一定的精度。
二.提出一个较为简单,但是很有代表性的一个问题:
d 2 y d t 2 = a y , 其 中 y ( 1 ) = 0.909 , y ( 1.1 ) = 0.706 \frac{d^2y}{dt^2}=ay, 其中y(1) = 0.909,y(1.1) = 0.706 dt2d2y=ay,其中y(1)=0.909,y(1.1)=0.706
其中, t t t每隔 0.1 0.1 0.1个长度的数据如下:
y r e a l = [ 0909 , 0.706 , 0.363 , 0.079 , − 0.226 , − 0.474 , − 0.765 , − 1.183 , − 1.436 , − 1.573 ] y_{real} = [0909,0.706,0.363,0.079,-0.226,-0.474,-0.765,-1.183,-1.436,-1.573] yreal=[0909,0.706,0.363,0.079,−0.226,−0.474,−0.765,−1.183,−1.436,−1.573]
求: a ^ \hat{a} a^
解决这类问题首先是不能用 m a t l a b matlab matlab的 o d e ode ode函数求解的,因为这是一个有 2 2 2点初值的问题,在 t = 1 t=1 t=1时刻 y y y的导数是不知道的。
三.求解的基本原理:
求解这个问题,而且包括更广放的一般的拟合问题,都要用到我们伟大的高斯老师的最小二乘法作为基本的工具。
m i n a ∈ R ∑ i = 1 n ( y c a l c ( i ) − y r e a l ( i ) ) 2 min_{a\in R}\sum_{i=1}^n(y_{calc}^{(i)}-y_{real}^{(i)})^2 mina∈Ri=1∑n(ycalc(i)−yreal(i))2
然而,要想求出计算值来实际上得先把这个微分问题转化为差分方程问题如下图:
h = 0.1 ; t 0 = 1 ; y t 0 = 0.909 , y t 0 + h = 0.706 y t + h + y t − h − 2 y t h 2 = a y t h = 0.1;t_0 = 1;y_{t_0} = 0.909,y_{t_0+h} = 0.706\\ \frac{y_{t+h}+y_{t-h}-2y_t}{h^2} = ay_t h=0.1;t0=1;yt0=0.909,yt0+h=0.706h2yt+h+yt−h−2yt=ayt
这样只要我们知道了 a a a的大小就可以把每一点的 y y y值算出来了。这样其实就转化成了一个求 a a a值的无约束单目标优化问题, 目标函数就是我们的最小二乘函数。
四.求解的基本算法:
1.利用 m a t l a b matlab matlab遗传算法求解出其最优误差函数值:
我们利用 m a t l a b matlab matlab自带的现成的 g a ga ga工具箱求解,基本的代码如下:
function err = obj_ode(a)
h = 0.1;
fun_ode = zeros(1,10);
real_value = [0.909 0.706 0.363 0.079 -0.226 -0.474 -0.765 -1.183 -1.436 -1.573];
fun_ode(1) = 0.909;
fun_ode(2) = 0.706;
for t = 3:10
fun_ode(t) = (a*h^2+2)*fun_ode(t-1)-fun_ode(t-2);
end
err = sum((fun_ode-real_value).^2);
end
上面的函数是为了求出 a a a值固定时候的误差大小,也就是我们的最小二乘函数,现在要使得这个函数最小,就应该在主函数里用遗传算法来求解:
clc,clear;
real_value = [0.909 0.706 0.363 0.079 -0.226 -0.474 -0.765 -1.183 -1.436 -1.573];
[a,error_value] = ga(@obj_ode,1);
f = @(t,u)[u(2);a*u(1)^2];
y_init = [0.909;(0.706-0.909)/0.1];
[u,y] = ode45(f,1:0.1:1.9,y_init);
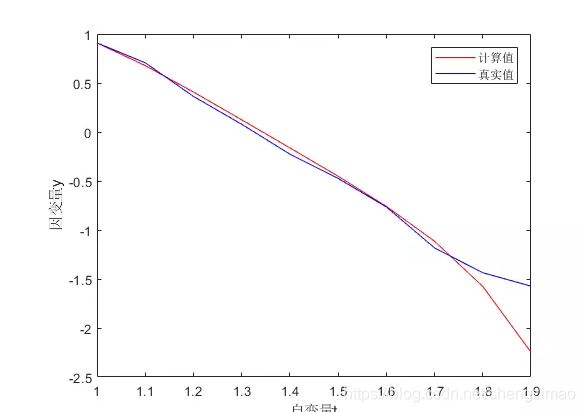
plot(1:0.1:1.9,y(:,1),'r-',1:0.1:1.9,real_value,'b-');
xlabel('自变量t');
ylabel('因变量y');
legend('计算值','真实值');
fprintf('a的值是:%f',a);
fprintf('最小误差的值是:%f',error_value);
求出来最后的拟合曲线如下:
求出来的 a a a是 − 8.13 -8.13 −8.13,误差在 0.49 0.49 0.49左右。但是从曲线上看貌似到最后误差变得有点大了。
2.差分后用 L I N G O LINGO LINGO求解:
model:
sets:
time/1..100/:t,y;!100等分点;
num/1..10/:y_real,y_calc;
endsets
data:
y_real=0.909 0.706 0.363 0.079 -0.226 -0.474 -0.765 -1.183 -1.436 -1.573;!实际值;
enddata
CALC:
h = 0.01;!步长;
y(1) = 0.909;
y(11) = 0.706;
endcalc
min = @sum(num:(y_real-y_calc)^2);
@for(time(i)|i#gt#2:y(i)=(a*h^2+2)*y(i-1)-y(i-2));!差分关系;
@for(num(i):y_calc(i) = y(10*(i-1)+1));!映射关系;
@free(a);
end
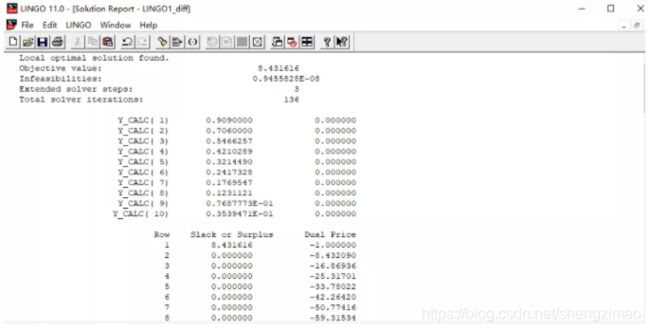
最后求出的结果如下:
求出的 a a a是 8.43 8.43 8.43,很明显示 L I N G O LINGO LINGO收敛到了局部最优解。没有得到我们想要的全局最优解。在这方面,遗传算法要比 L I N G O LINGO LINGO强上一些。
其实也可以尝试以下用4阶龙格库塔法编写 L I N G O LINGO LINGO求解,有尝试过的小伙伴可以自己比较一下结果哦!