基于遗传算法自动化集装箱码头多载AGV调度(一)—模型搭建
1.问题
1.1 问题背景
1.2 基本假设
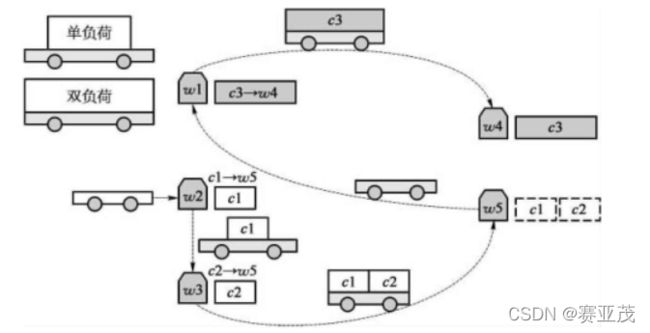
- 单辆多载AGV调度。
- 各个集装箱装载顺序不受时间限制,AGV可从任意任务起始点开始运输。
- 规划目标为运输时间最短。
- 每个任务有装载点和交付点。
| 任务数目 | N N N | N N N个任务全部装卸点 | I = { 1 , 2 , 3...2 N − 1 , 2 N } I=\{1,2,3...2N-1,2N\} I={1,2,3...2N−1,2N} |
|---|---|---|---|
| 虚拟起点 | 2 N + 1 2N+1 2N+1 | 运输任务 c 1 c_1 c1 | 20英尺集装箱 |
| 虚拟终点 | 2 N + 2 2N+2 2N+2 | 运输任务 c 2 c_2 c2 | 20英尺集装箱 |
| 任务点总数 | 2 N + 2 2N+2 2N+2 | 运输任务 c 3 c_3 c3 | 40英尺集装箱 |
2.模型建立与求解
2.1 符号说明
| 符号 | 说明 | 符号 | 说明 |
|---|---|---|---|
| 任务数目 | N N N | 运输任务装载点坐标 | P m P_m Pm |
| 任务装载点集合 | P P P | 运输任务交付点坐标 | D m D_m Dm |
| 任务交付点集合 | D D D | AGV运行速度 | θ \theta θ |
| 任务点总集合 | I = P ∪ D I=P \cup D I=P∪D | m m m 到$ n$点的运行时间 | T m , n T_{m,n} Tm,n |
| 增加虚拟起点与终点总集合 | I + = P ∪ D I^+=P \cup D I+=P∪D | AGV在任务点 m m m的容量改变情况 | d m d_m dm |
| 任务点 m m m的容量改变情况 | d m d_m dm | 任务点 m m m操作完成后AGV容量占用 | C m C_m Cm |
| AGV的最大负载能力 | C C C | 决策变量表示访问 m , n m,n m,n任务点 | x m n = 1 x_{mn}=1 xmn=1 |
| 决策变量AGV点 m m m完成操作时间 | z m z_m zm | 虚拟起点 | S S S |
| 虚拟终点 | E E E | 最末任务完成时间 | f f f |
2.2 调度模型
(1)目标函数 min f \min f minf
(2)约束条件
最末任务完成时间不小于任何事件的完成时间: f ≥ z m , ∀ m ∈ I f\geq z_m ,\forall m \in I f≥zm,∀m∈I。
若从任务点 m m m前往 n n n,则在时间上应该从m点装完货加上路程时间到达 n n n点后,才能开始取货交付:
z n + ( 1 − x m , n ) M l ≥ z m + T m n , ∀ m , n ∈ I , m ≠ n z_n+(1-x_{m,n})M_l\geq z_m+T_{mn},\forall m,n\in I,m\neq n zn+(1−xm,n)Ml≥zm+Tmn,∀m,n∈I,m=n
这里的要求是 M l M_l Ml是一个很大的数,取一个值 M l = ∑ i j T i j M_l=\sum_{ij}T_{ij} Ml=∑ijTij,这里的处理是很巧妙的。
从任意的任务装载点 m m m到任意的交付点之间是要走一段路程的:
z m + T m ( N + m ) ≤ z N + m , m ∈ P , N + m ∈ D z_m+T_{m(N+m)}\leq z_{N+m},m\in P,N+m\in D zm+Tm(N+m)≤zN+m,m∈P,N+m∈D
任意一个任务点 I I I一定只有一个前驱和后继。只有一个前驱说明,该任务点作为交付点时,只能被交付装载货物一次。只有一个后继 说明,该任务点作为装载点时,一次就能把货物全部全部放上装载AGV小车。
∑ m ∈ I + x m n = ∑ m ∈ I + x n m = 1 , ∀ n ∈ I \sum_{m \in I^+}x_{mn}=\sum_{m \in I^+}x_{nm}=1,\forall n \in I m∈I+∑xmn=m∈I+∑xnm=1,∀n∈I
而且对于这样一个小车而言,对于任何一条路线 m → n m\rightarrow n m→n或 n → m n\rightarrow m n→m,最多只能被小车遍历一次(AGV要么不走,否则绝对不走回头路):
x m , n + x n , m ≤ 1 , ∀ m , n ∈ I , m ≠ n x_{m,n}+x_{n,m}\leq 1,\forall m,n\in I,m\ne n xm,n+xn,m≤1,∀m,n∈I,m=n
考虑特殊的虚拟起点与终点情况,虚拟起点只有一个后继: ∑ n ∈ I + / S x S n = 1 \sum_{n\in I^+/S}x_{Sn}=1 ∑n∈I+/SxSn=1,同样虚拟终点只有一个前驱 ∑ m ∈ I + / E x m E = 1 \sum_{m\in I^+/E}x_{mE}=1 ∑m∈I+/ExmE=1。
如果AGV走 m , n m,n m,n任务点路线的话必定伴随两点之间货物容量的变化:
x m n ( C m + d n − C n ) = 0 , ∀ m , n ∈ I + x_{mn}(C_m+d_n-C_n)=0,\forall m,n\in I^+ xmn(Cm+dn−Cn)=0,∀m,n∈I+
以下是负载约束:
d m ≤ C m ≤ C , ∀ m ∈ P 0 ≤ C n ≤ C + d n , ∀ n ∈ D C S = C E = 0 , d_m\leq C_m \leq C,\forall m \in P\\ 0\leq C_n \leq C+d_n,\forall n \in D\\ C_S=C_E=0,\\ dm≤Cm≤C,∀m∈P0≤Cn≤C+dn,∀n∈DCS=CE=0,
下面是基本的参数变量的约束条件:
x m m = x m S = x E m = 0 , ∀ m ∈ I + f ≥ 0 , z m ≥ 0 , T m , n ≥ 0 , ∀ m , n ∈ I + x m n ∈ { 0 , 1 } , ∀ m , n ∈ I + x_{mm}=x_{mS}=x_{Em}=0,\forall m \in I^+\\ f\geq0,z_m \geq 0,T_{m,n}\geq0,\forall m,n \in I^+\\ x_{mn}\in \{0,1\},\forall m,n \in I^+ xmm=xmS=xEm=0,∀m∈I+f≥0,zm≥0,Tm,n≥0,∀m,n∈I+xmn∈{0,1},∀m,n∈I+