朴素贝叶斯案例分析
贝叶斯模型是利用先贝叶斯定理进行计算的一种机器学习模型,并且此处涉及先验概率和后验概率。比如我们都知道去赌场会十赌九输,此是以前的经验,即为先验概率,也或者大家都知道抛硬币时上下面第一次都是1/2概率,这均为先验概率;如果发现一个人准备跳楼,那么此时他是因为赌博导致的概率是多少?此为后验概率。有了先验概率和后验证概率理解,结合贝叶斯定量即可计算出概率信息值。
接着,朴素贝叶斯是基于贝叶斯定量,并且加上条件(特征之间独立)的一种模型。此处特征属性之间独立是指比如:有100个数据,第1行数据与第2行,第3行等其它任意行数据之间并没有关系,此前提条件非常重要,但现实中较难成立,但这并没有妨碍其的广泛使用,可能原因在于朴素贝叶斯模型通于分类问题处理,其内部算法上会关注于条件概率排序并非具体概率数字,因而其具有一定容错能力,并且特征属性之间假如有着关系并不完全独立,其内部可能存在相关抵消现象。整体上看,朴素贝叶斯模型原理较为简单,且应用较为广泛,比如输入法时可能会进行纠错功能处理,也或者垃圾邮件的识别等。
1 背景
案例数据依旧采用‘鸢尾花分类数据集’,其数据集为150个样本,包括4个特征属性(4个自变量X),标签为鸢尾花卉类别,其分为3个类别分别是刚毛鸢尾花、变色鸢尾花和弗吉尼亚鸢尾花(下称A、B、C三类)。
2 理论
朴素贝叶斯模型的原理较为简单,其利用贝叶斯概率公式,分别如下:
接着假定各特征属性独立,并且将公式进行展示成如下:
关于朴素贝叶斯模型时,其原理理解较为简单,但其内部算法上有着更多内容,感兴趣的读者可参阅下述页面,点击查看。
https://scikit-learn.org/stable/modules/naive_bayes.html
关于朴素贝叶斯参数上,其特征(自变量X)的数据分布对模型有着较大影响,如下表格说明:
如果特征即自变量X全部均为连续定量数据,那么选择高斯分布即可(此为默认值);如果说特征即自变量X中全部均是定类数据且每个X的类别数量大于2,此时可选择多项式分布。如果每个特征全部都是0和1共两个数字,此时选择伯努利分布。如果特征中即包括连续定量数据,又包括定类数据,建议可对定类数据进行哑变量设置后,选择高斯分布。
关于关于哑变量可点击查看。
http://spssau.com/front/spssau/helps/otherdocuments/dummy.html
3 操作
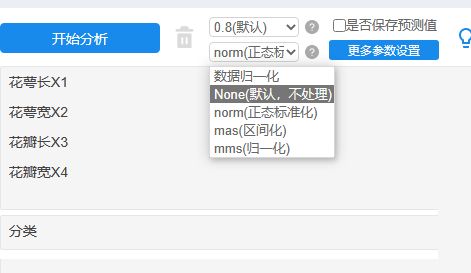
本例子操作如下:
训练集比例默认选择为:0.8即80%(150*0.8=120个样本)进行训练朴素贝叶斯模型,余下20%即30个样本(测试数据)用于模型的验证。需要注意的是,此处不进行处理也可以,尤其是自变量X中有定类数据是,建议默认不进行处理。
接着对参数设置如下:
本案例时四个自变量X(特征项)均为连续数据,因而默认为高斯分布即可;如果数据中包括定类数据,建议参考上一部分内容说明。
4 SPSSAU输出结果
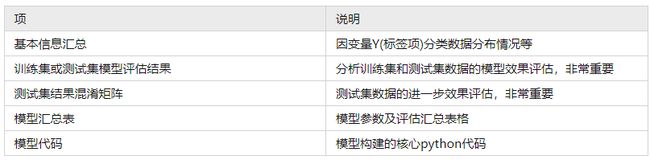
SPSSAU共输出5项结果,依次为基本信息汇总,训练集或测试集模型评估结果,测试集结果混淆矩阵,模型汇总表和模型代码,如下说明:
上述表格中,基本信息汇总表格展示因变量Y的分类数据分布情况,接着展示训练集和测试集效果情况,并且单独提供测试集数据混淆判断矩阵,进一步分析测试数据的正确效果等,模型汇总表格展示整体模型参数情况,并且提供sklean进行朴素贝叶斯模型构建的核心代码。
5文字分析
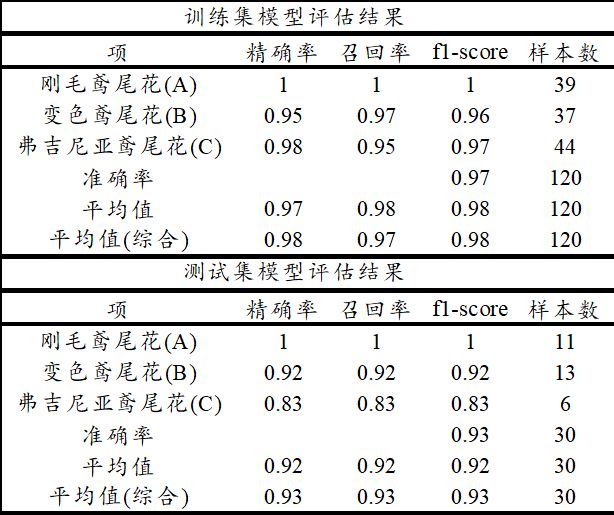
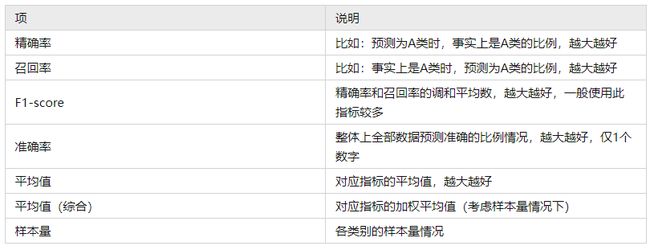
上表格中分别针对训练集和测试集,提供四个评估指标,分别是精确率、召回率、f1-scrore、准确率,以及平均指标和样本量指标等,如下表格说明:
一般来说,f1-score指标值最适合,因为其综合精确率和召回率两个指标,并且可查看其平均值(综合)指标,本案例为0.98,并且测试数据的表现上为0.93,意味着评估效果良好。
进一步地,可查看测试数据的‘混淆矩阵’,即模型预测和事实情况的交叉集合,如下图:
‘混淆矩阵’时,右下三角对角线的值越大越好,其表示预测值和真实值完全一致。本测试数据中有2个样本被判断类别出错,整体模型较优。
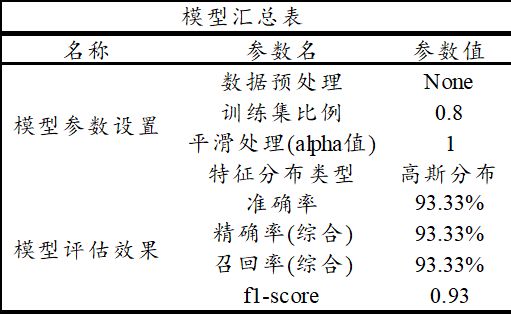
最后针对模型汇总表,其展示构建朴素贝叶斯模型各项参数设置,上表格中单独有输出平滑处理alpha值,当alpha=1.0时,称作Laplace平滑,当0 model = GaussianNB(alpha=1.0) model.fit(x_train, y_train) 涉及以下几个关键点,分别如下: 当前朴素贝叶斯模型支持分类任务,需要确保标签项(因变量Y)为定类数据,如果为定量连续数据,也或者样本量较少(或者非会员仅分析前100个样本)时可能出现无法计算因而提示数据质量异常。6 剖析
朴素贝叶斯模型时,其并不涉及距离等计算,不关注于数据的量纲情况,而只关注于各数据情况下的概率情况,因而通常不需要做任何处理。
如果数据量很大,比如1万,那么训练集比例可以较高比如0.9,如果数据量较小,此时训练集比例选择较小预留出较多数据进行测试即可。
保存预测值时,SPSSAU会新生成一个标题用于存储模型预测的类别信息,其数字的意义与模型中标签项(因变量Y)的数字保持一致意义。