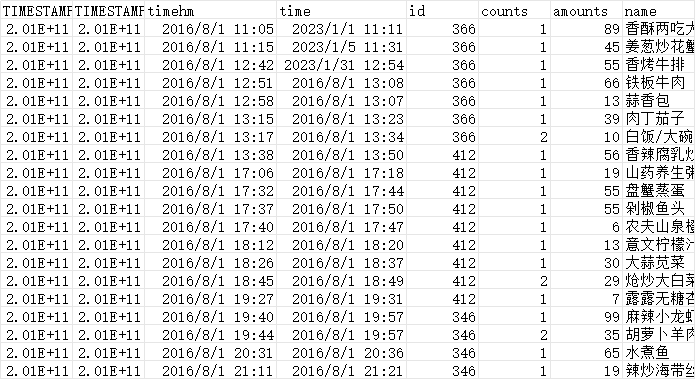
5.4 转换数据

数据集 E:/Input/ptest.csv

5.4.1 哑变量处理类别型数据

  数据分析模型中有相当一部分的算法模型都要求输入的特征为数值型，但实际数据中特征的类型不一定只有数值型，还会存在相当一部分的类别型，这部分的特征需要经过哑变量处理才可以放入模型之中。哑变量处理的原理示例如图：

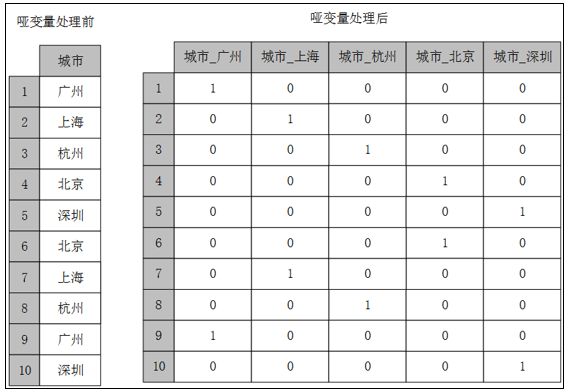
  Python中可以利用pandas库中的get_dummies函数对类别型特征进行哑变量处理

pandas.get_dummies(data, prefix=None, prefix_sep=‘_’, dummy_na=False, columns=None, sparse=False, drop_first=False)

import pandas as pd
import numpy as np
df = pd.read_csv('E:/Input/ptest.csv', encoding='gbk')
data = df['name'].head(5)
print(data)
print(pd.get_dummies(data))

  从结果中可以发现，对于一个类别型特征，若其取值有m个，则经过哑变量处理后就变成了m个二元特征，并且这些特征互斥，每次只有一个激活，这使得数据变得稀疏。
  对类别型特征进行哑变量处理主要解决了部分算法模型无法处理类别型数据的问题，这在一定程度上起到了扩充特征的作用。由于数据变成了稀疏矩阵的形式，因此也加速了算法模型的运算速度。

5.4.2 离散化连续型数据

  某些模型算法，特别是某些分类算法如ID3决策树算法和Apriori算法等，要求数据是离散的，此时就需要将连续型特征（数值型）变换成离散型特征（类别型）。
  连续特征的离散化就是在数据的取值范围内设定若干个离散的划分点，将取值范围划分为一些离散化的区间，最后用不同的符号或整数值代表落在每个子区间中的数据值。
  因此离散化涉及两个子任务，即确定分类数以及如何将连续型数据映射到这些类别型数据上。其原理如图：

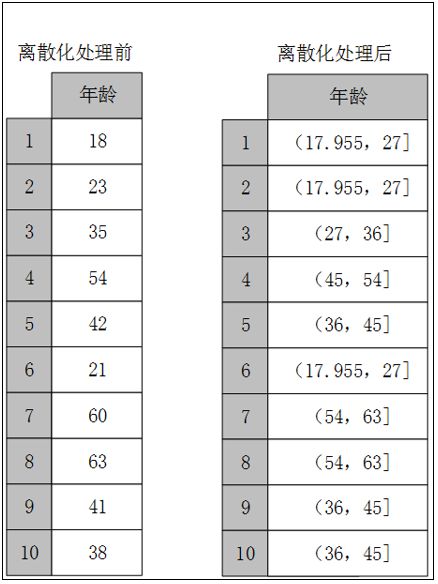
  常用的离散化方法主要有3种：等宽法、等频法和聚类分析法（一维）。

1、等宽法

  将数据的值域分成具有相同宽度的区间，区间的个数由数据本身的特点决定或者用户指定，与制作频率分布表类似。pandas提供了cut函数，可以进行连续型数据的等宽离散化，其基础语法格式如下。

pandas.cut(x, bins, right=True, labels=None, retbins=False, precision=3, include_lowest=False)

import pandas as pd
df = pd.read_csv('E:/Input/ptest.csv', encoding='gbk')
data = df['amounts']
# 1、等宽法
price = pd.cut(data, 5)
print(price.value_counts())

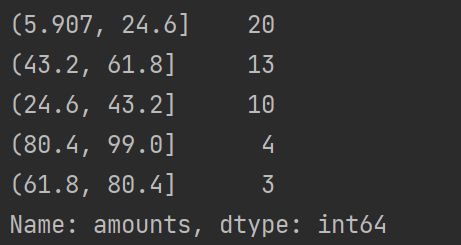
  使用等宽法离散化的缺陷为：等宽法离散化对数据分布具有较高要求，若数据分布不均匀，那么各个类的数目也会变得非常不均匀，有些区间包含许多数据，而另外一些区间的数据极少，这会严重损坏所建立的模型。

2、等频法

  cut函数虽然不能够直接实现等频离散化，但是可以通过定义将相同数量的记录放进每个区间。

import pandas as pd
import numpy as np
df = pd.read_csv('E:/Input/ptest.csv', encoding='gbk')
data = df['amounts']
# 2、等频法
# 自定义等频法离散化函数
def SameRateCut(data, k):
    w = data.quantile(np.arange(0,1+1.0/k, 1.0/k))
    data = pd.cut(data,w)
    return data
price = SameRateCut(data, 5)
print(price.value_counts())

  等频法离散化的方法相比较于等宽法离散化而言，避免了类分布不均匀的问题，但同时却也有可能将数值非常接近的两个值分到不同的区间以满足每个区间中固定的数据个数。

3、聚类分析法

  一维聚类的方法包括两个步骤：
   （1）将连续型数据用聚类算法（如K-Means算法等）进行聚类。
   （2）处理聚类得到的簇，将合并到一个簇的连续型数据做同一标记。
  聚类分析的离散化方法需要用户指定簇的个数，用来决定产生的区间数。

import pandas as pd
df = pd.read_csv('E:/Input/ptest.csv', encoding='gbk')

# 3、基于聚类分析的离散化
# 自定义数据K-Means聚类离散化函数
def KmeansCut(data, k):
    from sklearn.cluster import KMeans  # 引入K-Means
    # 建立模型
    kmodel = KMeans(n_clusters=k)
    kmodel.fit(data.values.reshape((len(data), 1)))
    # 输出聚类中心并排序
    c = pd.DataFrame(kmodel.cluster_centers_).sort_values(0)
    w = c.rolling(2).mean().iloc[1:]  # 相邻两项求中点，作为边界点
    w = [0] + list(w[0]) + [data.max()]  # 把首末边界点加上
    data = pd.cut(data,w)  #
    return data
data = df['amounts']
price = KmeansCut(data, 5)
print(price.value_counts())

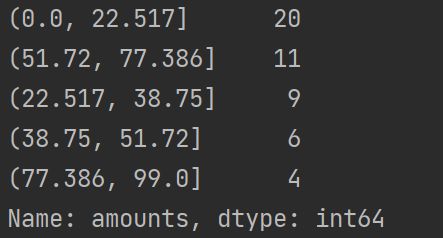
  k-Means聚类分析的离散化方法可以很好地根据现有特征的数据分布状况进行聚类，但是由于k-Means算法本身的缺陷，用该方法进行离散化时依旧需要指定离散化后类别的数目。此时需要配合聚类算法评价方法，找出最优的聚类簇数目。