逻辑回归：确定一个人是否年收入超过5万美元

1. 问题描述

学会使用学习到的逻辑回归的知识，手动使用梯度下降方法，通过给定的相关数据来完成年薪是否高于50k的二分类预测任务。

2. 设计简要描述

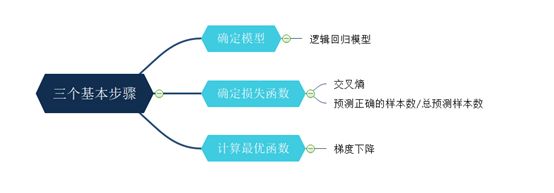
机器学习的三个基本步骤——

程序设计思路——(此图放大可看清)

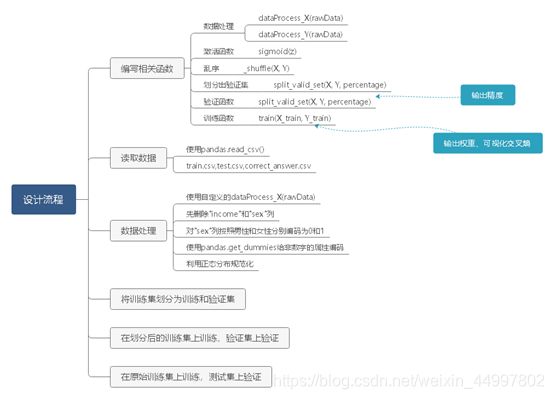
3. 程序清单

import pandas as pd
import numpy as np
from random import shuffle
from numpy.linalg import inv
import matplotlib.pyplot as plt
from math import floor, log
import os

output_dir = "output/"


def dataProcess_X(rawData):
    # sex 只有两个属性 先drop之后处理
    if "income" in rawData.columns:
        Data = rawData.drop(["sex", 'income'], axis=1)
    else:
        Data = rawData.drop(["sex"], axis=1)
    listObjectColumn = [col for col in Data.columns if Data[col].dtypes == "object"]  # 读取非数字的column
    listNonObjedtColumn = [x for x in list(Data) if x not in listObjectColumn]  # 数字的column

    ObjectData = Data[listObjectColumn]
    NonObjectData = Data[listNonObjedtColumn]
    # 将数字的column进行归一化： male = 0 以及 female = 1
    NonObjectData.insert(0, "sex", (rawData["sex"] == " Female").astype(np.int))
    # 给非数字的column每个属性一个编码
    ObjectData = pd.get_dummies(ObjectData)

    Data = pd.concat([NonObjectData, ObjectData], axis=1)  # axis=1就是以列为轴拼，横着拼
    Data_x = Data.astype("int64")
    # Data_y = (rawData["income"] == " <=50K").astype(np.int)

    # 利用正态分布来规范化
    Data_x = (Data_x - Data_x.mean()) / Data_x.std()

    return Data_x


def dataProcess_Y(rawData):
    df_y = rawData['income']
    Data_y = pd.DataFrame((df_y == ' >50K').astype("int64"), columns=["income"])  # 让"income"做表头
    return Data_y


# 将数据夹在[1e-8, 1-1e-8]之间
def sigmoid(z):
    res = 1 / (1.0 + np.exp(-z))
    # clip函数的作用：给定一个区间，区间外的值被剪切到区间边缘。
    return np.clip(res, 1e-8, 1 - 1e-8)


def _shuffle(X, Y):  # 打乱一列原先的顺序
    # arange()在给定的区间内返回间隔均匀的值
    randomize = np.arange(X.shape[0])
    # random.shuffle()作用是将序列原地洗牌
    np.random.shuffle(randomize)
    return (X[randomize], Y[randomize])


def split_valid_set(X, Y, percentage):  # 从训练集中分割出验证集
    all_size = X.shape[0]
    valid_size = int(floor(all_size * percentage))

    X, Y = _shuffle(X, Y)
    X_valid, Y_valid = X[: valid_size], Y[: valid_size]
    X_train, Y_train = X[valid_size:], Y[valid_size:]

    return X_train, Y_train, X_valid, Y_valid


def valid(X, Y, w):
    a = np.dot(w, X.T)
    y = sigmoid(a)
    y_ = np.around(y)  # around()函数作用 平均四舍五入到给定的小数
    result = (np.squeeze(Y) == y_)  # squeeze()的作用是变成一维
    print('acc = %f' % (float(result.sum()) / result.shape[0]))
    return y_  # 返回经过sigmoid函数的结果


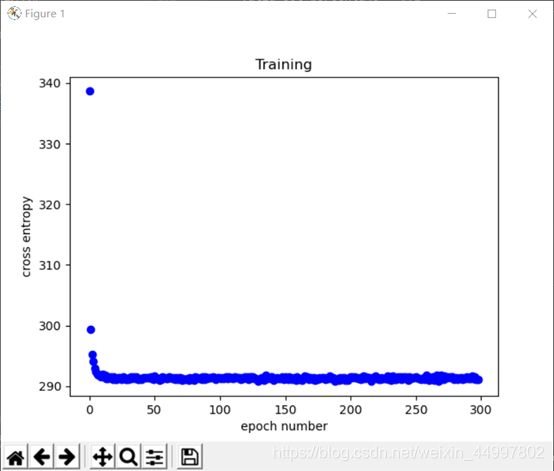
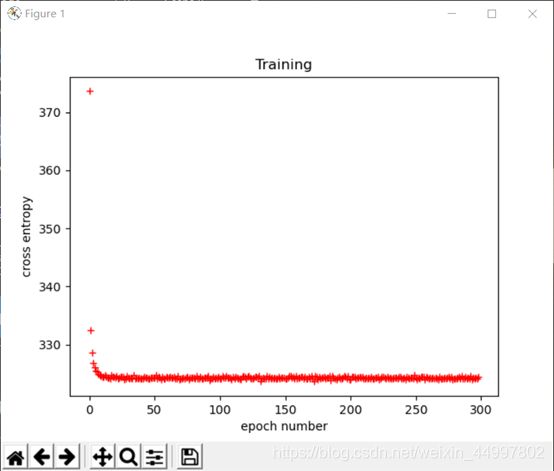
# 训练过程及可视化
def train(X_train, Y_train):
    w = np.zeros(len(X_train[0]))  # 列数

    l_rate = 0.001
    batch_size = 32
    train_dataz_size = len(X_train)  # 行数
    step_num = int(floor(train_dataz_size / batch_size))
    epoch_num = 300
    list_cost = []

    for epoch in range(1, epoch_num):
        total_loss = 0.0
        X_train, Y_train = _shuffle(X_train, Y_train)
        for idx in range(1, step_num):
            X = X_train[idx * batch_size:(idx + 1) * batch_size]
            Y = Y_train[idx * batch_size:(idx + 1) * batch_size]
            s_grad = np.zeros(len(X[0]))
            z = np.dot(X, w)
            y = sigmoid(z)
            loss = y - np.squeeze(Y)
            cross_entropy = -1 * (
                    np.dot(np.squeeze(Y.T), np.log(y)) + np.dot((1 - np.squeeze(Y.T)), np.log(1 - y))) / len(Y)
            total_loss += cross_entropy
            grad = np.sum(-1 * X * (np.squeeze(Y) - y).reshape((batch_size, 1)), axis=0)
            w = w - l_rate * grad
        list_cost.append(total_loss)
    plt.plot(np.arange(len(list_cost)), list_cost, 'r+')
    plt.title("Training")
    plt.xlabel("epoch number")
    plt.ylabel("cross entropy")
    plt.savefig(os.path.join(os.path.dirname(output_dir), "训练过程"))
    plt.show()

    return w


if __name__ == "__main__":
    trainData = pd.read_csv("data/train.csv")
    testData = pd.read_csv("data/test.csv")
    ans = pd.read_csv("data/correct_answer.csv")

    # drop函数默认删除行，列需要加axis = 1
    x_train = dataProcess_X(trainData).drop(['native_country_ Holand-Netherlands'], axis=1).values
    x_test = dataProcess_X(testData).values
    y_train = dataProcess_Y(trainData).values
    y_ans = ans['label'].values

    # concatenate()沿着一个现有的轴连接一个数组序列,axis=1表示纵轴
    x_test = np.concatenate((np.ones((x_test.shape[0], 1)), x_test), axis=1)
    x_train = np.concatenate((np.ones((x_train.shape[0], 1)), x_train), axis=1)

    # 从训练集中拿出10%的数据作为验证集
    valid_set_percentage = 0.1
    X_train, Y_train, X_valid, Y_valid = split_valid_set(x_train, y_train, valid_set_percentage)

    # 训练集上训练+训练集上验证
    print("训练集上训练+训练集上验证,结果如下")
    w_train = train(X_train, Y_train)
    valid(X_train, Y_train, w_train)

    # 原始训练集上训练+测试集上验证
    print("原始训练集上训练+测试集上验证,结果如下")
    w = train(x_train, y_train)
    y_ = valid(x_test, y_ans, w)

    df = pd.DataFrame({"id": np.arange(1, 16282), "label": y_})
    if not os.path.exists(output_dir):
        os.mkdir(output_dir)
    df.to_csv(os.path.join(output_dir + 'lr_output.csv'), sep='\t', index=False)

4. 结果分析

划分后的训练集上训练+验证集上验证

原始训练集上训练+测试集上验证

控制台输出

实验结果上下有浮动但浮动不大，因为每次从训练集中划分出验证集都是随机的。

5. 调试报告

1. 控制台报错AttributeError: module ‘sip’ has no attribute ‘setapi’
   查阅资料后发现是matplotlib包的版本不对，试图将其删除再装。由于是通过Pycharm自动安装，只会安装最新版本的。只好换了最初安装Python的解释器，可以在命令行通过pip install matplotlib==3.2 安装想要的版本。问题解决了。

6. 实验小结

1. 加深了对逻辑回归的理解
   与实验二相比，w和b是直接求得的，不基于任何概率分布假设。

2. 进一步理解了交叉熵
   即逻辑回归的损失函数
   
   括号中的两个可以可以看成是两个不同的伯努利分布
   
   
   分布P是人为定义的：
   样本属于Class1就记y ̂为1，属于Class就记y ̂为0
   而分布q则是函数集

3. 学到了一些数据处理函数/方法
   ①clip函数的作用：给定一个区间，区间外的值被剪切到区间边缘。
   ②arange()在给定的区间内返回间隔均匀的值
   ③random.shuffle()作用是将序列原地洗牌
   ④around()函数作用 平均四舍五入到给定的小数
   ⑤squeeze()的作用是将无论什么格式的数据变成一维
   ⑥drop函数默认删除行，列需要加axis = 1
   ⑦concatenate()沿着一个现有的轴连接一个数组序列,axis=1表示纵轴

4. 本次实验最大的收获是学会了查看官方文档，避免了原先的面向百度开发，受益匪浅。
   具体操作：在Pycharm上将光标移动到要查找的函数上方，shift+F1。

5. 本次实验和前几次不同的是使用了函数和可视化图表的方式。前者提高了代码的可复用性，后者增加了程序的友好程度。