环形子数组的最大和(medium)
题目链接:
918. 环形子数组的最大和
题目描述:
给定一个长度为
n的环形整数数组nums,返回nums的非空 子数组 的最大可能和 。环形数组 意味着数组的末端将会与开头相连呈环状。形式上,
nums[i]的下一个元素是nums[(i + 1) % n],nums[i]的前一个元素是nums[(i - 1 + n) % n]。子数组 最多只能包含固定缓冲区
nums中的每个元素一次。形式上,对于子数组nums[i], nums[i + 1], ..., nums[j],不存在i <= k1, k2 <= j其中k1 % n == k2 % n。示例 1:
输入:nums = [1,-2,3,-2] 输出:3 解释:从子数组 [3] 得到最大和 3示例 2:
输入:nums = [5,-3,5] 输出:10 解释:从子数组 [5,5] 得到最大和 5 + 5 = 10示例 3:
输入:nums = [3,-2,2,-3] 输出:3 解释:从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
题目解析
这道题比较麻烦,我们给定的数组实际上是一个不连续的,但是我们的在逻辑上要求他们连续.也就是最后一个元素之后,接着就是我们第一个元素.这里面要求我们的需要进行处理.这道题也是要求我们的求连续子数组的最大连续和.
算法原理
状态表示
按照经验,我们以...为结尾表示状态.
dp[i]:表示以i位置为结尾,我们最大子数组最大的连续和.
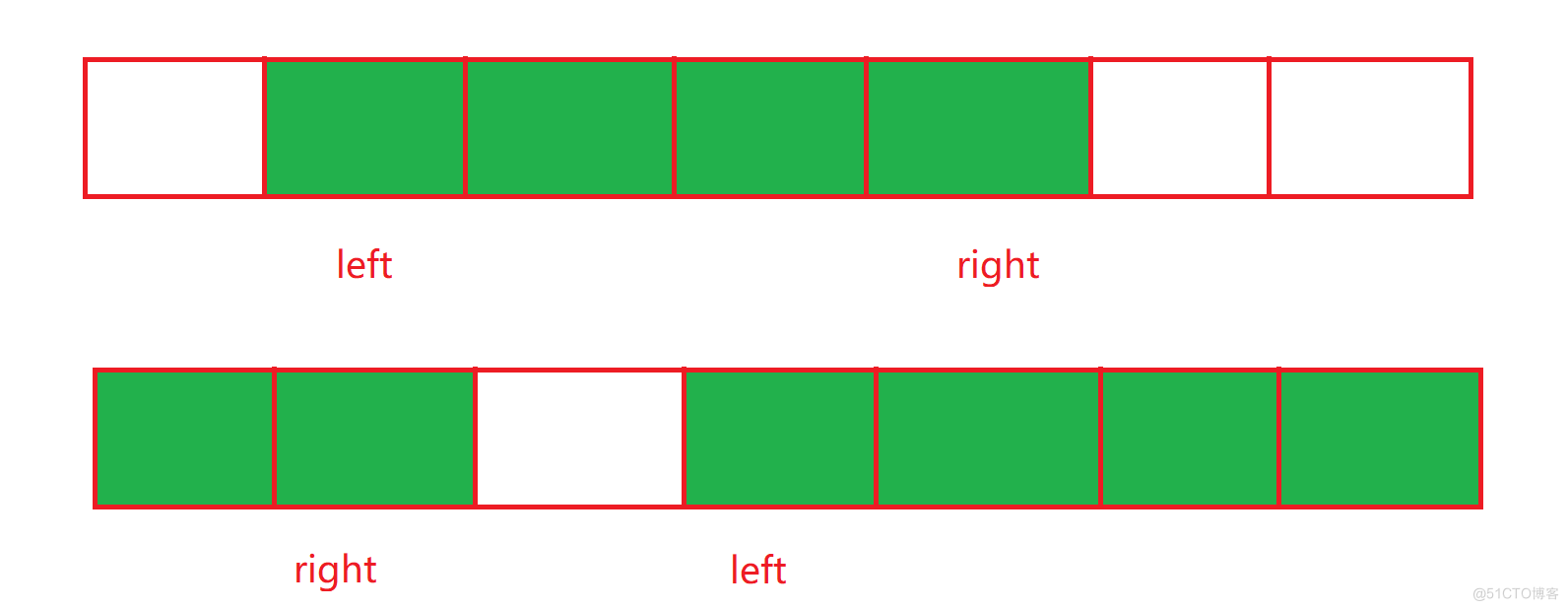
这道题优点问题,我们不知道数组什么时候结束.但是我们求连续子数组的最大和无非就是下面的两个情况.
那么此时我我们发现两个关键点.
- 对于情况1,我们求最大和就可以了
- 对于情况2, 我们整个数组的和是确定,求最大和,那么我们求最小的和不就可以吗,然后一减
此时定义两个状态
- f[i]: 表示以i位置,我们子数组的最大和
- g[i]: 表示以i位置,我们子数组的最小和
状态转移方程
我们只谈g[i].这里我们想一下.对于我们的nums[i].这里我们可以有两个选择.
- 选择nums[i]这一个元素作为我们的子数组 g[i]= nums[i]
- 和i-1联合作为子数组. g[i] = dp[i-1]+nums[i]
那么这里我们求最小值g[i] = min(nums[i], g[i]+nums[i]);
初始化
仍旧只谈给g[i].这里添加一个辅助节点.那么对于满足g[1]=v[0],只需要g[0]=0就可以了.
填表顺序
从左向右填,两个一起填.
返回值
三个变量,一个记录最大和,一个记录总和,一个记录最小和.我们返回最大和以及总和减去最小和的较大值.
编写代码
class Solution {
public:
int maxSubarraySumCircular(vector& nums) {
if(nums.empty())
return 0;
int n = nums.size();
vector f(n+1, 0);
vector g(n+1, 0);
int sum = 0;
int maxNum = INT_MIN;
int minNum = INT_MAX;
for(int i = 1; i <= n; i++)
{
sum += nums[i-1];
f[i] = std::max(f[i-1]+nums[i-1], nums[i-1]);
maxNum = std::max(maxNum, f[i]);
g[i] = std::min(g[i-1]+nums[i-1], nums[i-1]);
minNum = std::min(minNum, g[i]);
}
return max(maxNum, sum - minNum);
}
}; 这里我们发现错误,我们分析一下,主要是总和以及较小和.我们发现他们相等.也就是差值为0,但是我们整个数组都是负数,不能出现这种情况,那么此时我们就要排除一些这个情况.
class Solution {
public:
int maxSubarraySumCircular(vector& nums) {
if(nums.empty())
return 0;
int n = nums.size();
vector f(n+1, 0);
vector g(n+1, 0);
int sum = 0;
int maxNum = INT_MIN;
int minNum = INT_MAX;
for(int i = 1; i <= n; i++)
{
sum += nums[i-1];
f[i] = std::max(f[i-1]+nums[i-1], nums[i-1]);
maxNum = std::max(maxNum, f[i]);
g[i] = std::min(g[i-1]+nums[i-1], nums[i-1]);
minNum = std::min(minNum, g[i]);
}
if((sum - minNum) == 0)
return maxNum;
return max(maxNum, sum - minNum);
}
};