圆的反演 hdu 6158

欢迎关注更多精彩
关注我，学习常用算法与数据结构，一题多解，降维打击。

题目大意

http://acm.hdu.edu.cn/showproblem.php?pid=6158

给定2个相内切的圆，往两圆之间空隙处加入圆，依次加入，每次加入的圆尽可能大，求加入圆的总面积。

基本思路

圆的反演有如下性质：

1. 圆C的圆心为O，则如果有一个圆过点O，则该圆对C的反演是一条直线。反之直线可以反演成圆。
2. 如果两个圆相切，则反演后的几何形状还是相切。

根据题目的要求，每次加入的圆肯定与初始给定圆相切，也与之前加入过的最近的圆相切。
对这些圆进行反演后可以得到如下图形。

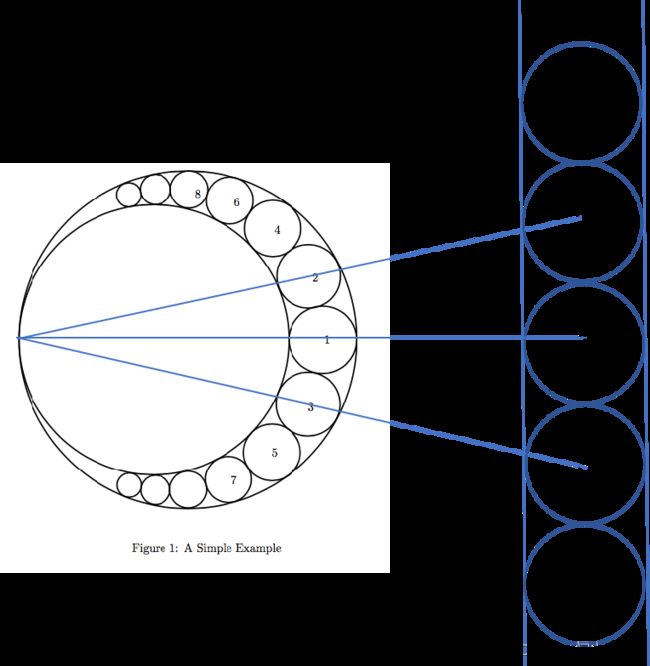
反演后的小圆是比较容易求得的。

错解

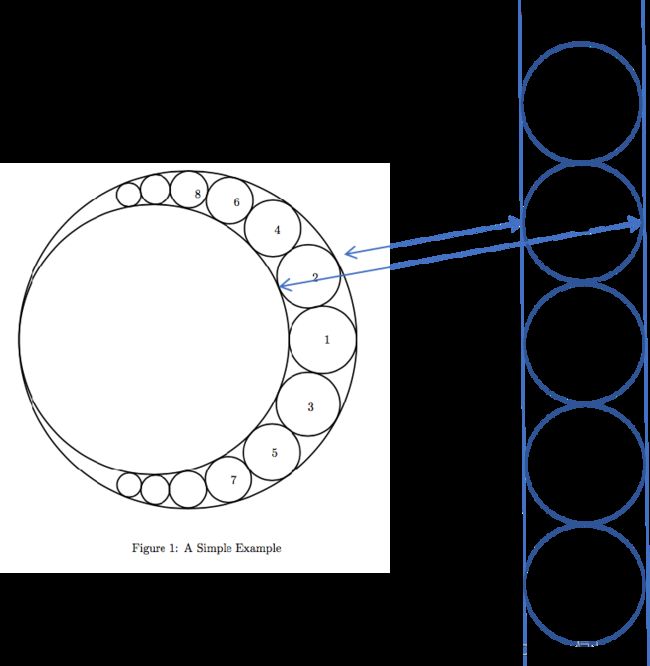
错解：对圆与直线切点进行反演作为直径的两点。
以圆2为例，对圆与直线两点进行反演得到的两点不能组成圆的直径。

证明如下：

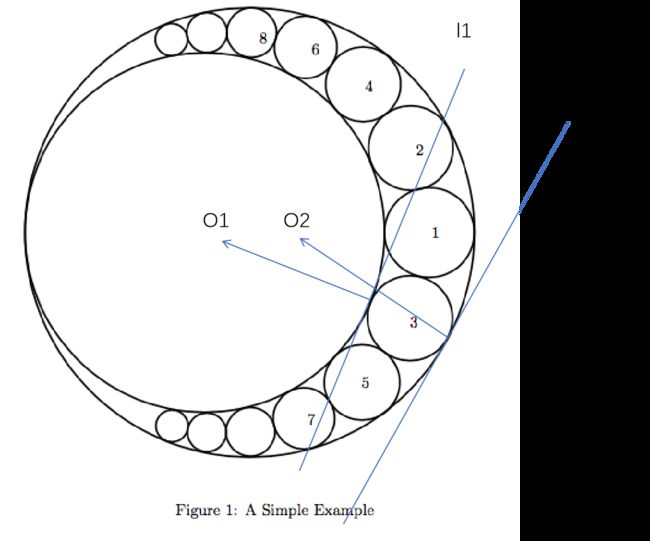
如果反演后的点可以构成直径，那么直径所在直线必然要经过相切圆的圆心，且与公切线垂直。
对圆与内圆和外圆的切点作公切线，公切线的法线肯定要过圆心。
两个公切线的法线分别经过O1和O2, O1和O2显然不是一个点。
也就是说反演后的点连线不能经过相切圆的圆心。

代码实现

#include
#include
#include 
#include 


using namespace std;

class Point {
public:
	double x, y;

	Point() {}
	Point(double a, double b) :x(a), y(b) {}
	Point(const Point &p) :x(p.x), y(p.y) {}

	void in() {
		scanf(" %lf %lf", &x, &y);
	}
	void out() {
		printf("%f %f\n", x, y);
	}

	double dis() {
		return sqrt(x * x + y * y);
	}

	Point operator -(const Point& p) const {
		return Point(x-p.x, y-p.y);
	}

	Point operator +(const Point& p) const {
		return Point(x + p.x, y + p.y);
	}
	Point operator *(double d)const {
		return Point(x *d, y *d);
	}

	Point operator /(double d)const {
		return Point(x / d, y / d);
	}


	void operator -=(Point& p) {
		x -= p.x;
		y -= p.y;
	}

	void operator +=(Point& p) {
		x += p.x;
		y += p.y;
	}
	void operator *=(double d) {
		x *= d;
		y *= d;
	}

	void operator /=(double d) {
		this ->operator*= (1 / d);
	}
};

class Line {
public:
	Point front, tail;
	Line() {}
	Line(Point a, Point b) :front(a), tail(b) {}
};

// https://oi-wiki.org//geometry/inverse/#%E5%8F%82%E8%80%83%E8%B5%84%E6%96%99%E4%B8%8E%E6%8B%93%E5%B1%95%E9%98%85%E8%AF%BB
// 根据官方定义实现圆的反演
class Circle
{
public:
	Point center;
	double r;
	
	Circle(const Point &c, double a):center(c), r(a){}
	Circle() {}
	void in() {
		center.in();
		scanf("%lf", &r);
	}
	void out() {
		center.out();
		printf("%f\n", r);
	}

	// 不过圆心的圆进行反演，得到1个圆
	Circle invert(const Circle& A) {
		Circle B;
		double oa = (center - A.center).dis();
		B.r = r * r / 2 * (1.0 / (oa - A.r) - 1.0 / (oa + A.r));
		double ob = r * r / (oa + A.r) + B.r;
		B.center = center +  (A.center - center)* ob / oa;
		return B;
	}

	// 过圆心的圆进行反演，得到1条直线
	Point invert2line(const Circle& c) {
		return Point();
	}	
	// 求反演点
	Point invertPoint(const Point &p) {
		Point dir = p - center;
		double dis = dir.dis();
		dir /= dis;
		dis = r * r / dis;
		return center + dir * dis;
	}
	
	// 直线反演，得到圆
	Circle invert2circle(const Line& l) {
		Point dir = l.front - l.tail;
		dir /= dir.dis();
		Circle c(Point(0, 0), 0);
		// 计算投影
		Point cdir = center - l.tail;
		Point project =l.tail + dir*(dir.x * cdir.x + dir.y*cdir.y);// 点乘得到投影长度

		// 计算圆到直线的距离
		Point op = project - center;
		if (op.dis() < 1e-6)return c;// 直线与圆心重合非法

		// 求解圆上的最远点
		double d = r * r / op.dis();
		Point pf = center + op / op.dis() * d;

		c.center = (center + pf) / 2;
		c.r = d / 2;

		return c;
	}

};

void solve() {
	Point P, Q, P1, Q1, M;
	int N;
	int T;
	Circle c1, c2,c1invert, c2invert, OC;
	OC.r = 100;
	int  r1, r2, x3, y3;
	double x1, x2;
	scanf("%d", &T);
	double PI = acos(-1);
	
	while(T--) {
		scanf("%d %d %d", &r1, &r2, &N);
		if (r1 == r2) {
			puts("0.00000");
			continue;
		}

		OC.center = Point(0,0);
		// 计算直线
		x1 = OC.r * OC.r / (r1 * 2);
		x2 = OC.r * OC.r / (r2 * 2);

		double d = abs(x1 - x2);

		double area = 0;
		double prearea = 100;
		for (int i = 0; i < N && prearea>1e-12;++i) {
			// 可以直接使用上1个
			if (i && (i % 2 == 0)) {
				area += prearea;
				continue;
			}
			
			c1.center = Point((x1+x2)/2, (i+1)/2*d);
			c1.r = d / 2;
			c1invert = OC.invert(c1);

			double r3 = c1invert.r;
			prearea = r3 * r3*PI;
			area += prearea;
		}

		printf("%.5f\n", area);
	}
}

int main() {
	solve();
	return 0;
}

/*
2
5 4
1
4 5
1

*/

---

本人码农，希望通过自己的分享，让大家更容易学懂计算机知识。