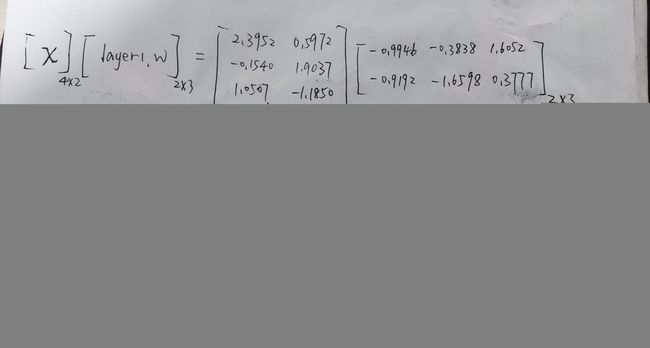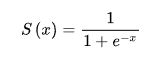pytorch 物体检测实战入门学习

        已经很久很久没有这样在心里有那种抑制不住的感伤，也很久没单独写过这样有些伤感的话了，从上上个星期上海疫情学校封闭，独自在上海自己租的房子里呆了已经有一个多星期了，再加上今天下午的飞机失事，一下子就会想起从慢慢懂事到现在这些年里发生了特别多的事，晚上学习到现在突然有点心理不知道是什么滋味而发愁、感叹和思绪万千。

        今天是个不太幸运的日子，作为一个什么也算不上的笔者（飞机下的中国人），真挚的希望在飞机上的132位同胞们能够平安，真挚的希望上海的疫情能够慢慢变好，希望世界的疫情能够慢慢变好，慢慢消失，希望存在的战争能够停止，这个世界的每一个人民都能平和的去拥抱和享受着和平而又美好的生活。

接下来进入正题

这个博客是记录为了做毕业设计，自己从零开始学习深度学习的一个入门博客，捣鼓很久有些地方没看明白，然后去问同学发现同学也不是很明白，所以只能自己熬夜摸索。

下面的代码主要是从深度学习之pytorch物体检测实战（刚开始看了前面一部分，个人这本书真的挺不错的，在这里要特别感谢我的大学朋友小胡给予的馈赠）第二章的pytorch基础部分

截屏的篇幅原因，无法截取所有代码，所以分多次截取，完整的代码在最下面有给出。

 

 

完整代码：

# 物体检测实战 p52

import torch
from torch import nn
import math

# 首先建立一个全连接的子module, 继承nn.Module
class Linear(nn.Module):
  def __init__(self, in_dim, out_dim):
    super(Linear, self).__init__()  #调用nn.Module的构造参数
    # 使用nn.Parameter来构造需要学习的参数
    self.w = nn.Parameter(torch.randn(in_dim, out_dim))
    self.b = nn.Parameter(torch.randn(out_dim))
  
  # 在forward 中实现前向传播过程
  def forward(self, x):             # 使用 Tensor.matmul 实现矩阵相乘
    x = x.matmul(self.w)            # 使用 Tensor.expand_as() 来保证矩阵形状一致
    print("x = ", x)
    y = x + self.b.expand_as(x)
    print("b = ", self.b.expand_as(x))
    print("y = ", y)
    print("ey = ", torch.exp(-y))
    return y
  
# 构建感知机类， 继承nn.Module， 并调用了 Linear 的子 module
class Perception(nn.Module):
  def __init__(self, in_dim, hid_dim, out_dim):
    super(Perception, self).__init__()
    self.layer1 = Linear(in_dim, hid_dim)
    self.layer2 = Linear(hid_dim, out_dim)

  def forward(self, x):
    x = self.layer1(x)
    y = torch.sigmoid(x)    # 使用Torch 中的sigmoid作为激活函数
    y = self.layer2(y)
    y = torch.sigmoid(y)
    return y


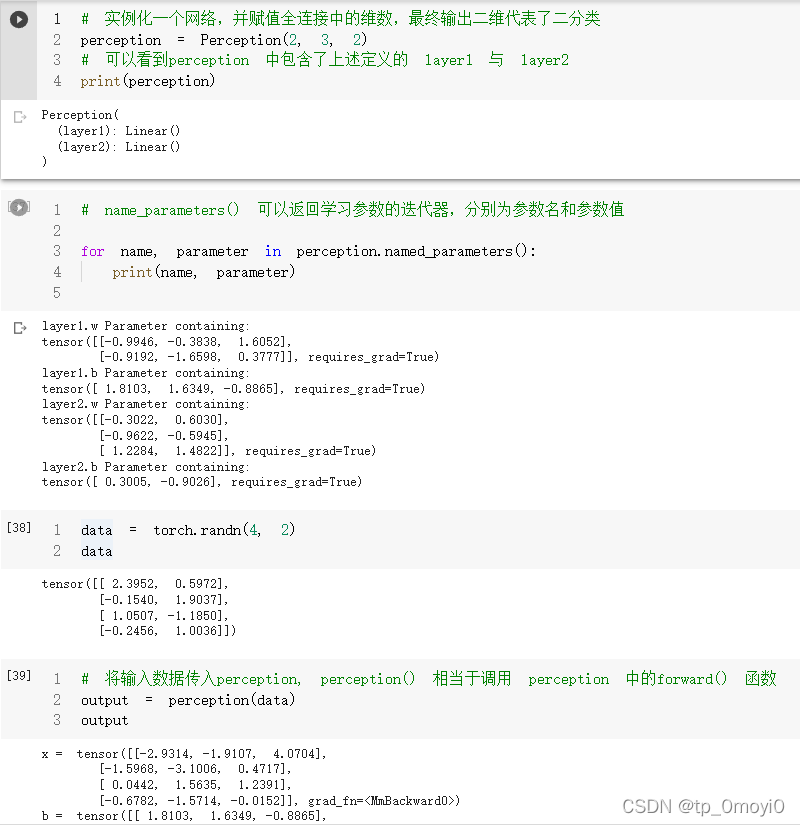
# 实例化一个网络，并赋值全连接中的维数，最终输出二维代表了二分类
perception = Perception(2, 3, 2)
# 可以看到perception 中包含了上述定义的 layer1 与 layer2
print(perception)

'''
Perception(
  (layer1): Linear()
  (layer2): Linear()
)
'''


# name_parameters() 可以返回学习参数的迭代器，分别为参数名和参数值

for name, parameter in perception.named_parameters():
  print(name, parameter)
 
'''
layer1.w Parameter containing:
tensor([[-0.9946, -0.3838,  1.6052],
        [-0.9192, -1.6598,  0.3777]], requires_grad=True)
layer1.b Parameter containing:
tensor([ 1.8103,  1.6349, -0.8865], requires_grad=True)
layer2.w Parameter containing:
tensor([[-0.3022,  0.6030],
        [-0.9622, -0.5945],
        [ 1.2284,  1.4822]], requires_grad=True)
layer2.b Parameter containing:
tensor([ 0.3005, -0.9026], requires_grad=True)
'''


data = torch.randn(4, 2)
data

'''
tensor([[ 2.3952,  0.5972],
        [-0.1540,  1.9037],
        [ 1.0507, -1.1850],
        [-0.2456,  1.0036]])
'''

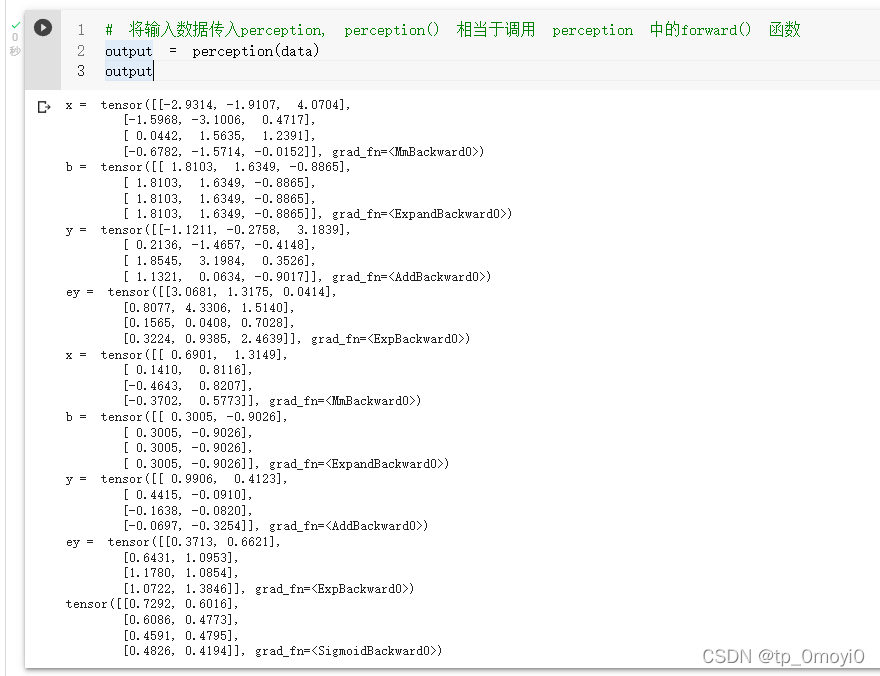
# 将输入数据传入perception, perception() 相当于调用 perception 中的forward() 函数
output = perception(data)
output

'''
x =  tensor([[-2.9314, -1.9107,  4.0704],
        [-1.5968, -3.1006,  0.4717],
        [ 0.0442,  1.5635,  1.2391],
        [-0.6782, -1.5714, -0.0152]], grad_fn=)
b =  tensor([[ 1.8103,  1.6349, -0.8865],
        [ 1.8103,  1.6349, -0.8865],
        [ 1.8103,  1.6349, -0.8865],
        [ 1.8103,  1.6349, -0.8865]], grad_fn=)
y =  tensor([[-1.1211, -0.2758,  3.1839],
        [ 0.2136, -1.4657, -0.4148],
        [ 1.8545,  3.1984,  0.3526],
        [ 1.1321,  0.0634, -0.9017]], grad_fn=)
ey =  tensor([[3.0681, 1.3175, 0.0414],
        [0.8077, 4.3306, 1.5140],
        [0.1565, 0.0408, 0.7028],
        [0.3224, 0.9385, 2.4639]], grad_fn=)
x =  tensor([[ 0.6901,  1.3149],
        [ 0.1410,  0.8116],
        [-0.4643,  0.8207],
        [-0.3702,  0.5773]], grad_fn=)
b =  tensor([[ 0.3005, -0.9026],
        [ 0.3005, -0.9026],
        [ 0.3005, -0.9026],
        [ 0.3005, -0.9026]], grad_fn=)
y =  tensor([[ 0.9906,  0.4123],
        [ 0.4415, -0.0910],
        [-0.1638, -0.0820],
        [-0.0697, -0.3254]], grad_fn=)
ey =  tensor([[0.3713, 0.6621],
        [0.6431, 1.0953],
        [1.1780, 1.0854],
        [1.0722, 1.3846]], grad_fn=)
tensor([[0.7292, 0.6016],
        [0.6086, 0.4773],
        [0.4591, 0.4795],
        [0.4826, 0.4194]], grad_fn=)

'''

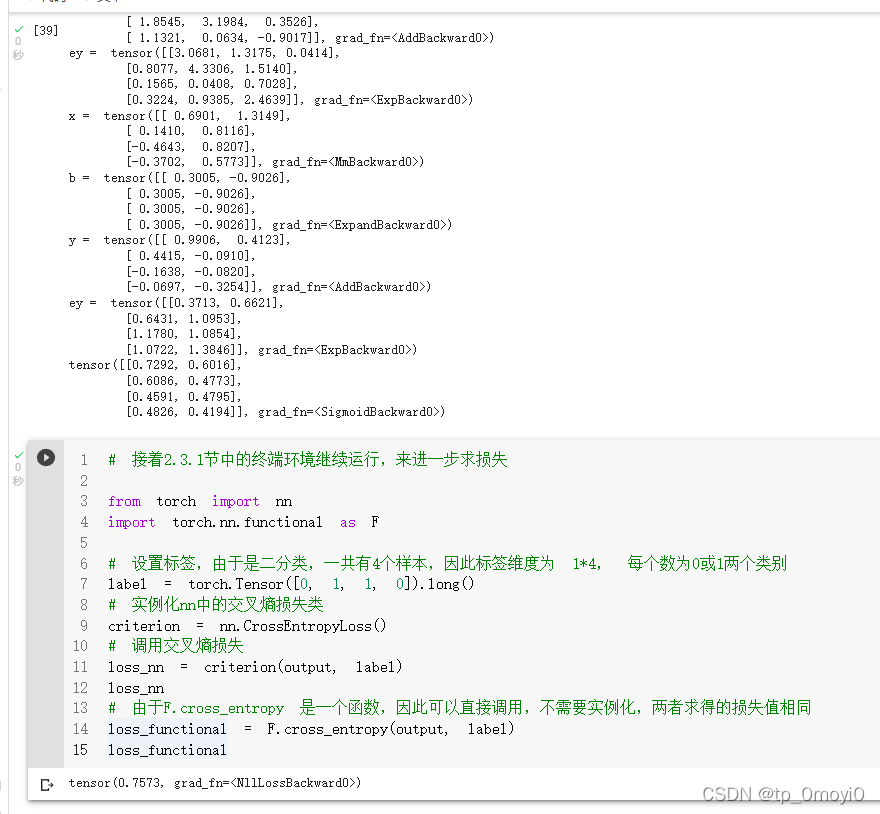
# 接着2.3.1节中的终端环境继续运行，来进一步求损失

from torch import nn
import torch.nn.functional as F

# 设置标签，由于是二分类，一共有4个样本，因此标签维度为 1*4， 每个数为0或1两个类别
label = torch.Tensor([0, 1, 1, 0]).long()
# 实例化nn中的交叉熵损失类
criterion = nn.CrossEntropyLoss()
# 调用交叉熵损失
loss_nn = criterion(output, label)
loss_nn
# 由于F.cross_entropy 是一个函数，因此可以直接调用，不需要实例化，两者求得的损失值相同
loss_functional = F.cross_entropy(output, label)
loss_functional

'''
tensor(0.7573, grad_fn=)
'''

主要定义的计算是

初始化输入data:

tensor([[ 2.3952,  0.5972],
        [-0.1540,  1.9037],
        [ 1.0507, -1.1850],
        [-0.2456,  1.0036]])

初始化 layer1.w

[[-0.9946, -0.3838,  1.6052],
 [-0.9192, -1.6598,  0.3777]]

初始化 layer1.b

[ 1.8103,  1.6349, -0.8865]

初始化 layer2.w

[[-0.3022,  0.6030],
 [-0.9622, -0.5945],
 [ 1.2284,  1.4822]]

初始化 layer2.b

[ 0.3005, -0.9026]

Linear这个类：   首先是建立一个全连接的子Moudle,继承nn.Module

主要进行的运算是 对于创建的输入的data进行运算

第一步：对输入的data即上面的 x 进行与随机生成的 w 进行矩阵乘法运算，并将矩阵运算后得到的结果在保存到  x

第二步：即对随机生成的 b 进行矩阵形状变换成和  经过第一步运算的获得的结果 x 一样的 shape,之后将随机生成的数据 b 和 x相加 得到 y

第三步： 返回 y

 Perception这个类：   然后是调用了上面的那个 Linear 类的子模块，构建了感知机类

主要进行的运算  即是 将传进的随机初始化 data 传入调用的 Linear 类中，进行两次 Linear 进行的相关运算，并在第一次和第二次之间加入 sigmoid 的激活函数。

图上的运算案例：

首先输入的  随机data为：

tensor([[ 2.3952,  0.5972],
        [-0.1540,  1.9037],
        [ 1.0507, -1.1850],
        [-0.2456,  1.0036]])

随机生成的 layer1.w 、layer1.b、layer2.w、layer2.b分别为

[[-0.9946, -0.3838,  1.6052],
 [-0.9192, -1.6598,  0.3777]]

[ 1.8103,  1.6349, -0.8865]

[[-0.3022,  0.6030],
 [-0.9622, -0.5945],
 [ 1.2284,  1.4822]]

[ 0.3005, -0.9026]

输入的data是一个 4 * 2 大小的二位张量

先与 大小为  2 * 3  的二维张量 layer1.w 进行矩阵乘法运算，所得结果为

计算过程部分如下：

得到 第一部分计算后的结果

[[-2.9314, -1.9107,  4.0704],
 [-1.5968, -3.1006,  0.4717],
 [ 0.0442,  1.5635,  1.2391],
 [-0.6782, -1.5714, -0.0152]]

之后与 layer1.b 进行 矩阵相加运算

先将 layer1.b 进行shape变换到和 x 同样的二维

[[ 1.8103,  1.6349, -0.8865],
 [ 1.8103,  1.6349, -0.8865],
 [ 1.8103,  1.6349, -0.8865],
 [ 1.8103,  1.6349, -0.8865]

 之后进行相加得到  y

[[-1.1211, -0.2758,  3.1839],
 [ 0.2136, -1.4657, -0.4148],
 [ 1.8545,  3.1984,  0.3526],
 [ 1.1321,  0.0634, -0.9017]]

之后  Perception 类对于 Linear 调用后返回的 y  再通过sigmoid 激活函数进行  sigmoid 的激活

这里在介绍一下  sigmoid 激活函数

 经过sigmoid激活后得到  （这部分忘记输出了，所以自己手动算了，可能会有误差）

[[0.2458, 0.4315, 0.9603],
 [0.5532, 0.1876, 0.3978],
 [0.8647, 0.9608, 0.5873],
 [0.7562, 0.5159, 0.2887]]

之后开始将这个进行输入到 Linear 开始第二轮和上面一样的运算

...

...

...

最后得到  输入

[[0.7292, 0.6016], 
 [0.6086, 0.4773], 
 [0.4591, 0.4795], 
 [0.4826, 0.4194]]