【python函数】torch.nn.Embedding函数用法图解

  学习SAM模型的时候，第一次看见了nn.Embedding函数，以前接触CV比较多，很少学习词嵌入方面的，找了一些资料一开始也不是很理解，多看了两遍后，突然顿悟，特此记录。

  SAM中PromptEncoder中运用nn.Embedding：

point_embeddings = [nn.Embedding(1, embed_dim) for i in range(self.num_point_embeddings)]

  torch.nn.Embedding官方页面

1. torch.nn.Embedding介绍

（1）词嵌入简介

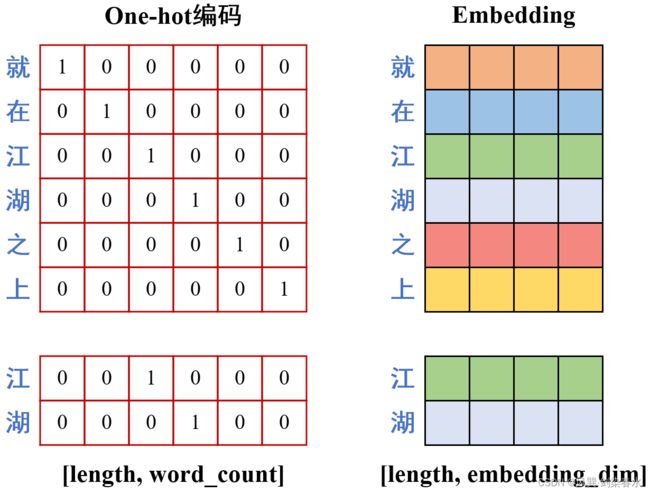
  关于词嵌入，这篇文章讲的挺清楚的，相比于One-hot编码，Embedding方式更方便计算，例如在“就在江湖之上”整个词典中，要编码“江湖”两个字，One-hot编码需要 $[length,word\_count]$ 大小的张量，其中 $word\_count$ 为词典中所有词的总数，而Embedding方式的嵌入维度 $embedding\_dim$ 可远远小于 $word\_count$ 。在运用Embedding方式编码的词典时，只需要词的索引，下图例子中： “江湖”——>[2, 3]

（2）重要参数介绍

  nn.embedding就相当于一个词典嵌入表：

torch.nn.Embedding(num_embeddings, embedding_dim, padding_idx=None, max_norm=None, norm_type=2.0, scale_grad_by_freq=False, sparse=False, _weight=None, _freeze=False, device=None, dtype=None)

常用参数：
  ① num_embeddings (int)： 词典中词的总数

  ② embedding_dim (int)： 词典中每个词的嵌入维度

  ③ padding_idx (int, optional)： 填充索引，在padding_idx处的嵌入向量在训练过程中没有更新，即它是一个固定的“pad”。对于新构造的Embedding，在padding_idx处的嵌入向量将默认为全零，但可以更新为另一个值以用作填充向量。

输入：$Input(\ast )$: IntTensor 或者 LongTensor，为任意size的张量，包含要提取的所有词索引。
输出：$Output(\ast ,H)$: $\ast$ 为输入张量的size，$H$ = embedding_dim

2. torch.nn.Embedding用法

（1）基本用法

官方例子如下：

import torch
import torch.nn as nn

embedding = nn.Embedding(10, 3)
x = torch.LongTensor([[1, 2, 4, 5], [4, 3, 2, 9]])

y = embedding(x)

print('权重:\n', embedding.weight)
print('输出:')
print(y)

查看权重与输出，打印如下：

权重:
 Parameter containing:
tensor([[ 1.4212,  0.6127, -1.1126],
        [ 0.4294, -1.0121, -1.8348],
        [-0.0315, -1.2234, -0.4589],
        [ 0.6131, -0.4381,  0.1253],
        [-1.0621, -0.1466,  1.7412],
        [ 1.0708, -0.7888, -0.0177],
        [-0.5979,  0.6465,  0.6508],
        [-0.5608, -0.3802, -0.4206],
        [ 1.1516,  0.4091,  1.2477],
        [-0.5753,  0.1394,  2.3447]], requires_grad=True)
输出:
tensor([[[ 0.4294, -1.0121, -1.8348],
         [-0.0315, -1.2234, -0.4589],
         [-1.0621, -0.1466,  1.7412],
         [ 1.0708, -0.7888, -0.0177]],

        [[-1.0621, -0.1466,  1.7412],
         [ 0.6131, -0.4381,  0.1253],
         [-0.0315, -1.2234, -0.4589],
         [-0.5753,  0.1394,  2.3447]]], grad_fn=<EmbeddingBackward0>)

  家人们，发现了什么，输入 $x$ 的 $size$ 大小为 $[2,4]$ ，输出 $y$ 的 $size$ 大小为 $[2,4,3]$ ，下图清晰的展示出nn.Embedding干了个什么事儿：

  nn.Embedding相当于是一本词典，本例中，词典中一共有10个词 $X_0$~$X_9$，每个词的嵌入维度为3，输入 $x$ 中记录词在词典中的索引，输出 $y$ 为输入 $x$ 经词典编码后的映射。

  注意：此时存在一个问题，词索引是不能超出词典的最大容量的，即本例中，输入 $x$ 中的数值取值范围为 $[0,9]$。

（2）自定义词典权重

  如上所示，在未定义时，nn.Embedding的自动初始化权重满足 $N(0,1)$ 分布，此外，nn.Embedding的权重也可以通过from_pretrained来自定义：

import torch
import torch.nn as nn

weight = torch.FloatTensor([[1, 2.3, 3], [4, 5.1, 6.3]])
embedding = nn.Embedding.from_pretrained(weight)
x = torch.LongTensor([1, 0, 0])
y = embedding(x)
print(y)

输出为：

tensor([[4.0000, 5.1000, 6.3000],
        [1.0000, 2.3000, 3.0000],
        [1.0000, 2.3000, 3.0000]])

（3）padding_idx用法

  padding_idx可用于指定词典中哪一个索引的词填充为0。

import torch
import torch.nn as nn

embedding = nn.Embedding(10, 3, padding_idx=5)
x = torch.LongTensor([[5, 2, 0, 5]])
y = embedding(x)
print('权重:\n', embedding.weight)
print('输出:')
print(y)

输出为：

权重:
 Parameter containing:
tensor([[ 0.1831, -0.0200,  0.7023],
        [ 0.2751, -0.1189, -0.3325],
        [-0.5242, -0.2230, -1.1677],
        [-0.4078, -1.2141,  1.3185],
        [ 0.8973, -0.9650,  0.5420],
        [ 0.0000,  0.0000,  0.0000],
        [ 0.0597,  0.6810, -0.2595],
        [ 0.6543, -0.6242,  0.2337],
        [-0.0780, -0.9607, -0.0618],
        [ 0.2801, -0.6041, -1.4143]], requires_grad=True)
输出:
tensor([[[ 0.0000,  0.0000,  0.0000],
         [-0.5242, -0.2230, -1.1677],
         [ 0.1831, -0.0200,  0.7023],
         [ 0.0000,  0.0000,  0.0000]]], grad_fn=<EmbeddingBackward0>)

  词典中，被padding_idx标定后的词嵌入向量可被重新定义：

import torch
import torch.nn as nn

padding_idx=2
embedding = nn.Embedding(3, 3, padding_idx=padding_idx)
print('权重:\n', embedding.weight)

with torch.no_grad():
    embedding.weight[padding_idx] = torch.tensor([1.1, 2.2, 3.3])
print('权重:\n', embedding.weight)

输出为：

权重:
 Parameter containing:
tensor([[ 0.7247,  0.7553, -1.8226],
        [-1.3304, -0.5025,  0.5237],
        [ 0.0000,  0.0000,  0.0000]], requires_grad=True)
权重:
 Parameter containing:
tensor([[ 0.7247,  0.7553, -1.8226],
        [-1.3304, -0.5025,  0.5237],
        [ 1.1000,  2.2000,  3.3000]], requires_grad=True)