Distill学习计划-GNN的通俗解释
A Gentle Introduction to Graph Neural Networks
译自非常好的一篇博客，原文链接
本文旨在探索如何利用图的结构和特性构建出图神经网络(graph neural network,GNN)，并探索其设计结构背后的动机和原理，最后抛出该研究领域的相关问题。
下图表示在图中每个节点如何通过层次去聚集信息。
Chapter1 简言
图数据对我们非常重要，因为现实中物体之间总有着千丝万缕的联系，有联系的物体集合我们可以表示为一张图。目前GNN发展了十余年，我们已经能够看到其在抗菌发现、物理模拟、假新闻检测、流量预测和推荐系统方面的应用了。
我们将用以下四部分解释现代GNN：
- 探究选用哪种可以表示为图的数据，并举一些通俗的例子
- 探究图在哪方面有别于其他类型的数据，以及处理这些数据的特殊选择
- 构建一个现代GNN，并遍历模型的每个部分。
- 提供一个GNN交互能使你处理现实世界的任务和数据集，以建立一个更强的直觉，了解GNN模型的每个组件如何对它的预测做出贡献。(请跳转到原文)
Chapter2 准备工作
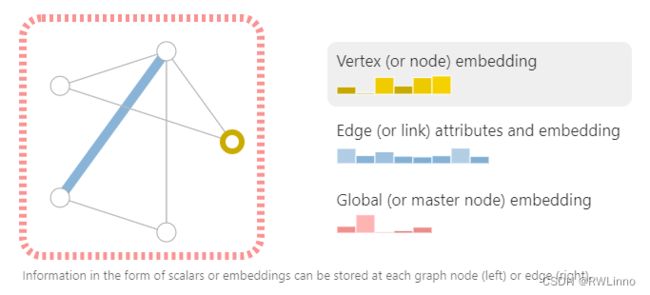
首先，我们的Graph表示为
何种数据可表示为图
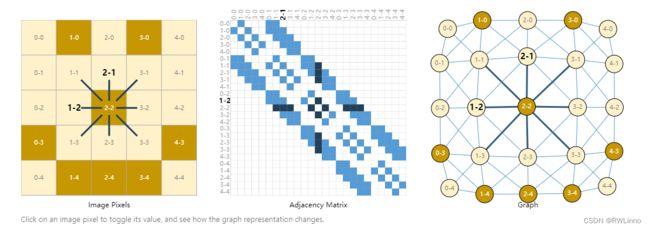
- 图像：我们知道图像可以表示为二维矩阵的多通道叠加，每个像素点可看作是结点存储颜色信息，往相邻8个像素进行连边，图像就可以转化为图结构。
-
文字：通过文字序列的词和索引当作结点，其前后关系指向看作边，可以转化为图结构。
当然，事实上用图表示这些数据是冗余的，因为图和文本都有很规整的结构。这只是为了说明图是很强力的数据结构来表示诸如此类以外的很多东西。下面我们来展示图所表示的更为异构的数据。
- 分子结构：在三维空间中，原子通过共价键形成了稳定距离的连接，那么我们可以构建出相应的图结构来表示。
- 社交网络：社交网络是研究人们、机构和组织的集体行为模式的工具。我们可以通过将个体建模为节点，将他们的关系建模为边来构建一个表示人群的图。
- 引用网络：科学家在发表论文时经常引用其他科学家的研究成果。我们可以将这些引用网络可视化成一个图，其中每篇论文是一个节点，每个有向边是一篇论文和另一篇论文之间的引用。此外，我们可以在每个节点中添加关于每篇论文的信息，例如摘要的词嵌入。
Chapter3 图结构所解决的任务
在图结构的预测任务上，有图级、点级和边级之分。图/点/边级的任务上，主要侧重点便是预测图/点/边的一些性质。GNN可以解决这三级的问题。
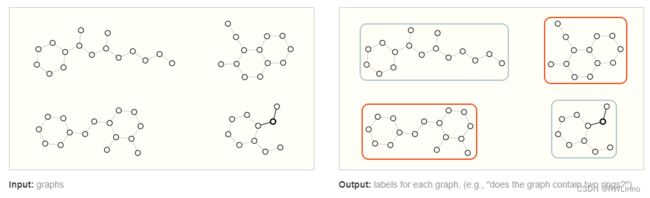
Graph-Level：与MNIST和CIFAR的图像分类任务类似，我们希望将整个图关联到一个标签上，应用到文本上大概就类似情感识别任务。
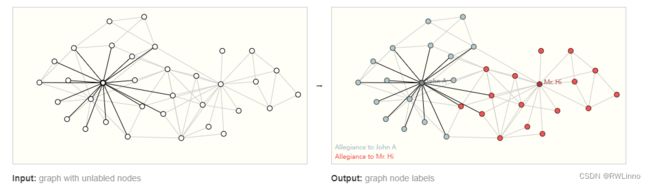
Node-Level：以下是典型的例子：扎克的空手道俱乐部。通过社交网络去预测每个成员所属的俱乐部。在图像领域，这相当于分割任务，而在文本上相当于预测每个单词的词性。
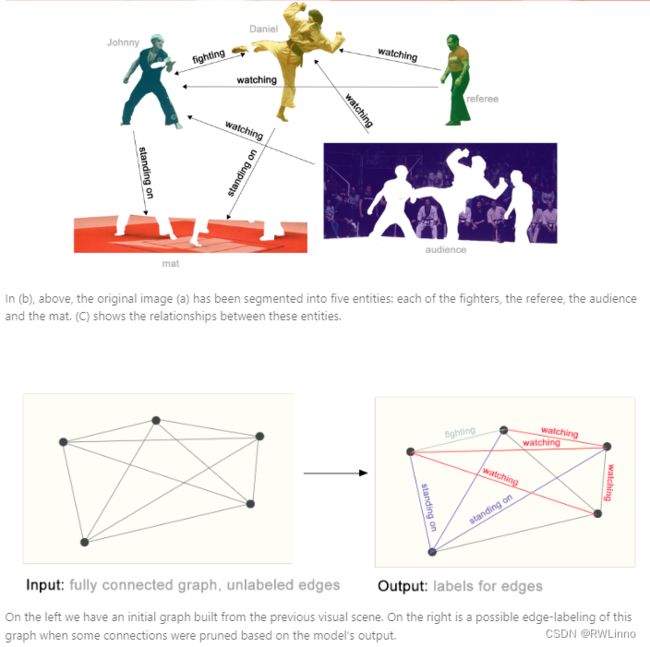
Edge-Level：典型的例子是图像场景理解，除了识别对象以外，我们可进一步理解它们的关系，并预测对象相互的一些行为。
Chapter4 在机器学习中使用图的挑战
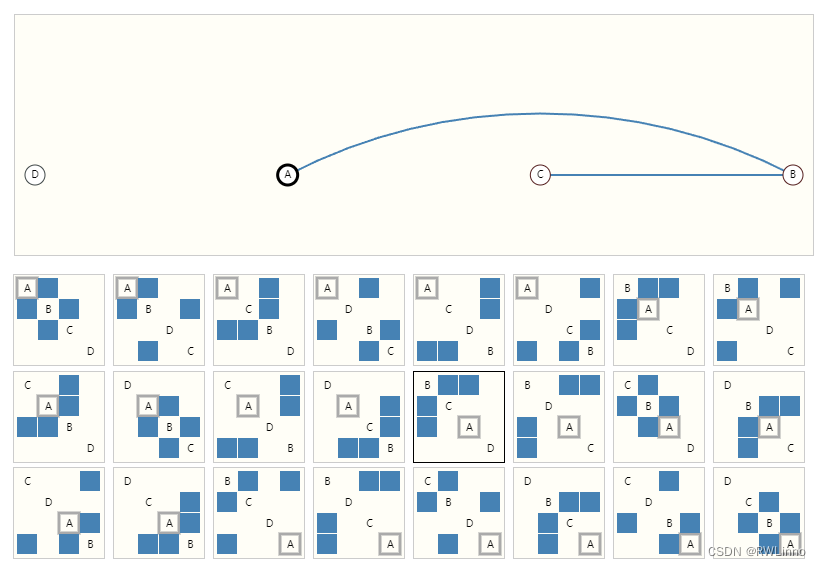
使用神经网络解决不同的图上问题的第一步就是如何表示与神经网络兼容的图。机器学习通常采用的是规整或格状的数据，而图至少存储点、边、全局信息和相关性。对于前三种是比较简单的，可以不用其他特殊技术就转换为机器学习的输入。而相关性相对复杂一些，最显然的选择是邻接矩阵。而这种表示存在一些短板：
-
有成千上万节点的稀疏图上，邻接矩阵的信息是很冗余的。在n=4的情况下就有了24种矩阵表示
-
很多邻接矩阵可以编码成相同的相关信息，却不能保证不同矩阵产生相同结果。
一种避免这些短板的方法是采用邻接表
Chapter5 GNN的构建
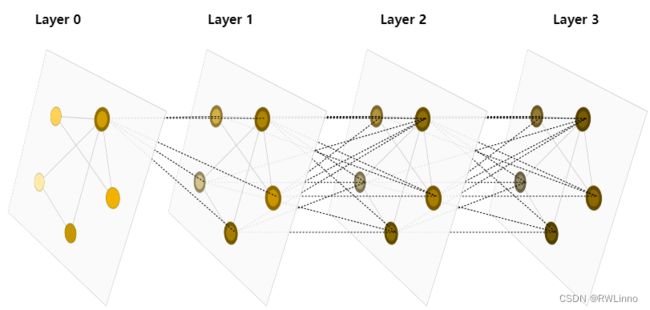
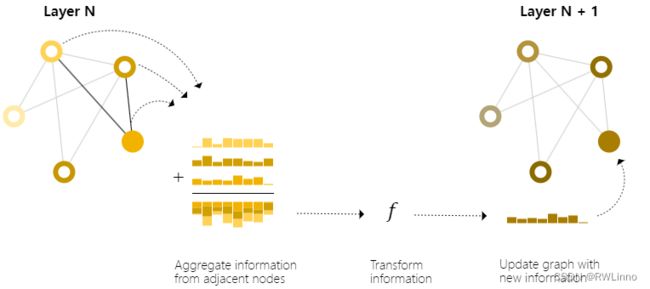
现在既然图的描述是排列不变的矩阵格式，我们就可以使用图神经网络(gnn)来解决图预测任务了。 GNN 是对图的所有属性(节点、边、全局上下文)进行优化转换，以保持图的对称性(置换不变性)。
最简单的形式
在此我们不考虑图上的相关信息，从点、边和全局信息出发，在图的每个部分使用独立的多层感知机(MLP)，称为GNN的一层。我们的MLP返回的是经过学习的点向量、边向量以及全局信息向量，这样就相当于对整个图学习了单一层的嵌入向量。simple GNN的一层表示如下：
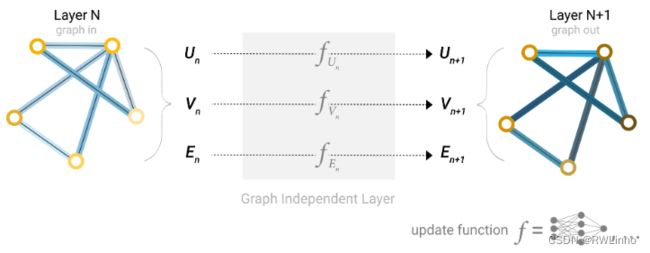
跟普通神经网络一样，我们可以把GNN层堆叠起来。在GNN不更新关联信息的前提下，我们将使用与输入相同的邻接表和相同数量的特征向量作为输出，但是输出图已经更新了嵌入，因为GNN已经更新了每个节点、边缘和全局上下文表示。
通过汇聚信息进行GNN预测
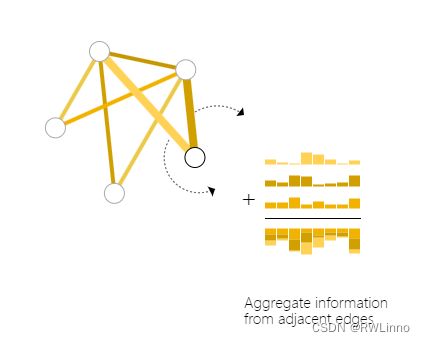
通常我们需要一种从邻边收集信息到点上做预测的方法，我们可以用**池化(Pooling)**来做（类似于CNN中的全局平均池化），分为以下两步：
-
对于所有需要池化的物体，收集它们的每个嵌入并将它们连接到一个矩阵中。
-
通过求和聚合收集的嵌入。
不管我们拥有的是点级的信息还是边级的信息，我们都可以这样转换。同理对于边预测任务也可以这样做。也就是说我们可以建立一个简单的GNN模型，并通过在图的不同部分之间路由信息来进行二分类预测。这种池化技术将作为构建更复杂的GNN模型的基础。如果我们有新的图形属性，我们只需要定义如何将信息从一个属性传递到另一个属性。
在这个最简单的GNN公式中，我们在GNN层中根本没有使用图的连通性。每个节点、每条边以及全局上下文都是独立处理的。我们只在汇集信息进行预测时使用连通性。
在图的各部分之间传递信息
我们可以使用一种叫message passing的技术使相邻节点和边相互交换信息并影响其他的已更新嵌入向量。步骤如下：
- 对图中的每个结点收集邻点嵌入向量信息(用g表示)
- 通过聚合函数(比如sum)来聚集信息
- 使用计算函数f来池化信息（通常是一个经过学习的神经网络）
跟前面一样，如果我们数据只有边的信息，我们可以采用与前面使用相邻节点信息相同的方法合并来自相邻边的信息，首先将边信息池化，用更新函数对其进行转换然后存储，从而对其他信息进行预测(比如节点分类)。但是存储在图中的点和边不一定是相同的大小或形状，因此如何将它们组合起来并不是很明确。一种方法是学习从边空间到节点空间的线性映射，或者可以在更新函数之前将它们连接在一起。
在构造GNN中我们选何种方法、以怎样的顺序嵌入信息是一个较为开放的研究领域。比方说我们有’weave’ fashion的更新方式，对新的点边可以四种更新表示：node to node (linear), edge to edge (linear), node to edge (edge layer), edge to node (node layer).
添加全局信息表示
即便多次使用message passing，我们描述的网络仍有着较远节点无法有效传递信息的缺陷。对k层的网络，信息最多会传递到k步远，而对于以一组点为单位的预测任务来说这会是个问题。一种解决方法是使信息在所有点之间传递，而这对很大的图来讲这会是代价昂贵的（一种叫虚边的方式被应用在小型图比方说分子方面）
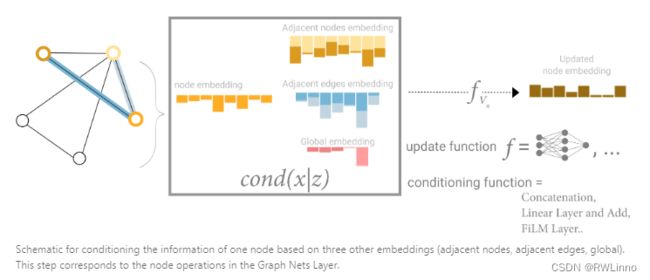
我们使用一种叫master node或者context vector的全局表示方法处理，即存在一个vector连接网络中所有节点和边，作为桥梁他可以传递信息并建立图整体的表示，这使图的表示能更加复杂和丰富。在这机制下更新信息由邻点邻边和全局信息三部分组成，我们可以简单使用线性映射投射到同一特征空间中，这被视为一种特征注意力机制。
Chapter6 GNN playground
请大家移步到原文，互动对于理解上述内容会很有帮助。同时非常感谢distill的高质量文章，鄙人翻译也许不太精确。
Chapter7 研究思路
1. 不同类型的图
- 多重图：一对节点可以共享多种类型的边
- 超图：一条边可以连接到多个节点
- 超节点：图中的一个节点可以表示一个图（也叫嵌套图）
- 分层图：拥有层次结构
2.图的采样和批处理
- 创建子图
- 随机抽取均匀数量的节点
- 随机采样单个节点，将其邻域扩展到距离k在扩展集中选点。
- Cluster-GCN和GraphSaint等策略
3.归纳偏置
- 图对称性（保持操作排列不变性）
4.选择和设计聚合操作
- 可微分方法
- 平滑聚合
- 方差统计
5.GCN作子图函数逼近器
- k个节点的子图学习嵌入
6.边和图对偶
- 利用对偶图求解边分类问题
7.卷积到矩乘到图上游走
- 将步数k转化为邻接矩阵的k次幂以表示在图上可达区域
8.图注意力网络
采用注意力机制(QKV)，将节点用线性的向量空间表示其，各点可以用内积同步更新参数。与Transformer不同的使GAN(Graph Attention Networks)要关注稀疏的网络。
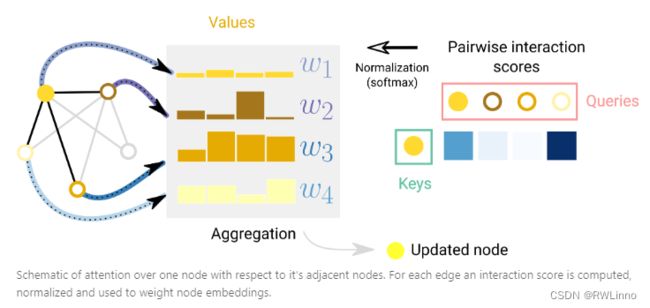
9.图解释性和归因
因为图存在很多概念和性质，我们关心特定图形的可解释性，可从上下文信息、子图存在与否或是连通程度进行解释。
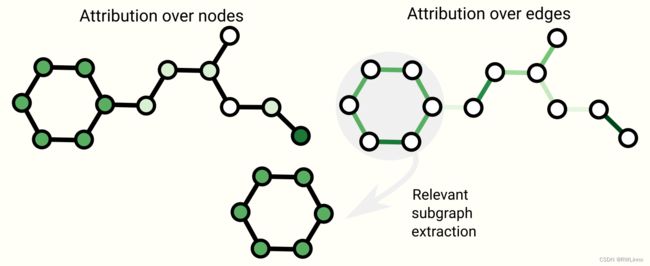
10.生成模型
-
通过学习分布采样或者给定起点，我们可以生成新图。这在新药设计中具有很大前景(构造图)。
-
关键挑战在于对图的拓扑进行建模，图的大小可能变化很大，一种解决方案是将邻接矩阵直接建模为带有自动编码器框架的图像。
-
构造顺序图：可以用自回归模型(如RNN)或强化学习场景