Distill学习计划-深入理解图上卷积

Understanding Convolutions on Graphs

译自非常好的一篇博客，原文链接

​ 很多系统和交互——社交网络、分子结构、组织机构、文献引用、物理模型和交通都可以表示为图。我们如何在这些系统中推理和做出预测？

​ 一种想法是我们应用在其他领域表现良好的工具，比如神经网络在许多学习任务中展示了巨大的潜力。但是传统神经网络常用于操作固定大小或者常规结构的输入（比方说句子、图片和视频），因此我们不能优雅的用它们处理图结构数据。

​ 图神经网络(Graph neural networks,GNN)是神经网络中可用于处理图结构数据的一员，通过提取和利用基础图中的特征，GNN可以做出比起考虑单个实体的模型更明智的预测。

​ GNN不是可建模图结构数据的唯一工具,图核以及随机游走也是非常流行的方式。然如今GNN以其与生俱来的灵活性对基础图更好的建模方式而取代了其他这些技术。

​ 在这篇文章，我们阐述图上计算的挑战以及GNN的起源和设计，进而探索如今最流行的GNN变体，并且我们也会讨论这些变体是由哪些相似的模块组成的。

图上计算的挑战

缺乏一致结构

图通常是非常灵活的数学模型，而这也意味着它们不同实例间缺乏一致的结构，从以下例子就一目了然：

• 分子间有不同数量的原子
• 分子中的原子有不同的类型
• 每对原子可能有不同的连接方式
• 这些连接的引力可能不相同

以一种可计算的格式表示这些图的意义非同小可，而最终选择的表示通常很大程度上取决于实际问题。

节点顺序同变性

扩展上面一点：图上的节点在表示时通常没有固定顺序，因此我们想要我们的算法是顺序同变的，即它们不应该依赖节点顺序，如果我们以某种方式排序节点，那么最终的节点表示也应该以这种方式排序节点。

可测量性

图有时会很大，比方说Facebook和Twitter中超过了一亿用户，要操作这么大的数据非常不容易。而幸运的是，大多数自然产生的图都是稀疏的，也就是说点和边倾向于线性相关。我们发现这让我们可以使用聪明的方法去更高效的计算图中节点的表示。而这些方法有比起操作整个图会有更少的参数，这是非常重要的特性。

问题设置和标记

​ 图可以表示许多有用的问题，把覅是节点分类、图分类、节点聚类、链路预测、影响力最大化(重心)

​ 节点的表示学习是解决这些问题的共同前提：学习将这些单独的节点映射到固定大小的实值向量(嵌入/表示)。

​ 不同的GNN变体在计算这些表示的方式上会有所区别。然而通常来讲这个计算是一个迭代的过程。我们用$h_v^{(k)}$来表示经过$k^{th}$次迭代后节点v的表示，每次迭代都可以看作是标准神经网络中的一层。

​ 我们通常以字母$G$表示图，$V$表示点集，$E$表示边集。节点v以个体特征值作为部分输入，记为$x_v,v\in V$。比方说彩图中一个像素点的节点特征可能是它的RGB值。

​ 为了便于说明，我们假设$G$是无向的，并且每个点都是同种类型。这种图通常称为同构的。有时我们需要用矩阵$M$来表示图的特征，行$M_v$表示节点v的特征值。

扩展卷积到图领域

​ CNN是在图像上提取特征的强力工具，而图像本身可以被视为非常规律的格状结构，以像素表示节点，，和RGN通道值表示节点特征。

​ 那么一个自然而然的想法就是将卷积推广到任意图。我们首先介绍在节点邻域上构造多项式滤波器的想法，就像 CNN 在邻近像素上计算局部滤波器一样。然后，我们将看到这个想法如何用更新的方法去扩展成更强大的机制。最后，我们将讨论使用“全局”图级信息来计算节点表示的替代方法。

图上多项式滤子

拉普拉斯图

我们先为图$G$定义邻接矩阵A，度数矩阵$D$,使每一行$D_v={\sum }_u{A}_{vu}$,其中$A_{vu}$对应v行u列，拉普拉斯矩阵$L=D-A$

拉普拉斯多项式

​ 拉普拉斯图的多项式表示为$p_w(L)=w_0{I}_n+w_{1}L+w_2{L}^2+...+w_d{L}^d={\sum }_{i=0}^d{w}_i{L}_i$，每条多项式可以转化为系数向量$w=[w_0,...,w_d]$，那么对于每个w,$p_w(L)$也像$L$一样是一个$n\times n$的矩阵。

​ 这些多项式可以考虑为CNN中卷积核的等价物，系数$w$则是卷积核中的参数。为了便于说明，我们考虑节点特征只有1维的情况(在多维情况下是同样适用的)，我们把每个节点的特征值$x_i\in {\mathbb{R}}^n$张成向量$x$，定义通过卷积核$p_W$的卷积为$x^{\prime }=p_w(L)x$。

​ 考虑最简单的情况，$w_0=1$且其他系数为0，那么$x^{\prime }=x$。现在我们增加了度数，比方说$w_1=1$，那么$x^{\prime }=Lx$，因此
$$\begin{gathered} x_v^{\prime }=(Lx{)}_v=L_{v}x=\sum _{u\in G}{L}_{vu}{x}_u \\ =\sum _{u\in G}(D_{vu}-A_{vu})x_u=D_v{x}_v-\sum _{u\in \mathcal{N}(v)}{x}_u \end{gathered}$$
我们看到所有节点$v$都直接跟它的邻居$u\in \mathcal{N}(v)$结合特征。对熟悉图像拉普拉斯滤波器的同学，这是同样的方法和结果。那么多项式中的度数$d$又是如何影响卷积操作的。首先观察拉普拉斯矩阵上的性质$dis{t}_G(u,v)>i\Rightarrow L_{vu}^i=0$,这意味着我们用度数为$d$的多项式卷x时
$$\begin{gathered} x_v^{\prime }=(p_w(L)x{)}_v=(p_w(L){)}_{v}x=\sum _{i=0}^d{w}_i{L}_v^{i}x \\ =\sum _{i=0}^d{w}_i\sum _{u\in G}{L}_{vu}^i{x}_u=\sum _{i=0}^d{w}_i\sum _{u\in G\&dis{t}_G(u,v)\le i}{L}_{vu}^i{x}_u \end{gathered}$$
实际上，节点v处的卷积只发生在距离不超过d跳的节点u上，因此，这些多项式卷积核是局部的，位置信息由度数来决定。

ChebNet

ChebNet改进了多项式滤子的形式：$p_w(L)={\sum }_{i=1}^d{w}_i{T}_i(\tilde{L})$,其中$T_i$表示度为i的第一类切比雪夫不等式，$\tilde{L}$表示最大特征值定义的归一化拉普拉斯：$\tilde{T}=\frac{2L}{{\lambda }_{max}(L)}-I_n$（分析感兴趣可见原文）

多项式滤子是节点顺序等变的

这个在多项式$p_w$的度为1的时候显而易见：所有点特征都由邻居特征的加和汇聚，显然这个加和与顺序是没有关系的。

嵌入的计算

我们现在描述如何将 ChebNet (或其他多项式滤波器)层层叠加非线性来构建图神经网络，这跟标准的CNN差不多。特别的，如果我们由K层不同的滤波器，记$k^{th}$层可学习权重为$w^{(k)}$,我们计算过程如下：

• 初始状态：$h^{(0)}=x$
• 迭代K轮，第$k=1,2,...,K$轮时：
  • 从参数$L$中估算的权重$w$计算多项式：$p^{(k)}=p_{w^{(k)}}(L)$
  • p和h矩乘：$g^{(k)}=p^{(k)}\times h^{(k-1)}$
  • 引入非线性项：$h^{(k)}=\sigma (g^{(k)})$

注意，这些网络在不同的节点上重用相同的滤波器权值，正好模仿了卷积神经网络(CNN)中的权值共享，这种神经网络在网格上重用卷积滤波器的权值。

现代GNN网络

ChebNet在学习局部滤子上取得了突破，也激励了很多从不同角度对图上卷积的思考。我们回到多项式卷积核$p_w(L)=L$卷$x$的结果，注意到特别对节点v，有
$$\begin{gathered} (Lx{)}_v=L_{v}x=\sum _{u\in G}{L}_{vu}{x}_u \\ =\sum _{u\in G}(D_{vu}-A_{vu})x_u \\ =D_v{x}_v-\sum _{u\in \mathcal{N}(v)}{x}_u \end{gathered}$$
这是一跳的局部卷积，但重要的是我们可以把这种卷积视为由两个步骤产生：

• aggregation: 聚合直接近邻的特征$x_u$
• combination: 结合节点自身的特征$x_v$

如果我们考虑不同类型的“聚合”和“组合”步骤，超越了使用多项式过滤器的可能性，会怎样？

通过保证聚合是节点顺序可变的，整个卷积过程都是节点顺序可变的；这些卷积会被视为相邻节点之间的信息传递，每一步每个节点会从邻点收到信息，通过迭代k次一跳的卷积，卷积的接收域包括了所有节点k跳能到达的范围。

嵌入计算

信息传递建立了目前很多GNN框架的骨干网络，最流行的有以下几种：

• Graph Convolutional Networks(GCN)
  • $h_v^{(k)}=f^{(k)}(W^{(k)}\frac{{\sum }_{u\in \mathcal{N}(v)}{h}_u^{(h-1)}}{|\mathcal{N}(v)|}+B^{(k)}{h}_v^{(k-1)})$
• Graph Attention Networks(GAT)
  • $h_v^{(k)}=f^{(k)}(W^{(k)}[{\sum }_{u\in \mathcal{N}(v)}{\alpha }_{vu}^{(k-1)}{h}_u^{k-1}+{\alpha }_{vv}^{(k-1)}{h}_v^{(k-1)}])$
  • ${\alpha }_{vu}^{(k)}=\frac{A^{(k)}(h_v^k,h_u^{(k)})}{{\sum }_{w\in \mathcal{N}(v)}{A}^{(k)}(h_v^{(k)},h_w^{(k)})}$
• Graph Sample and Aggregate(GraphSAGE)
  • $h_v^{(k)}=f^{(k)}(W^{(k)}[AG{G}_{u\in \mathcal{N}(v)}(\{h_u^{(k-1)}\}),h_v^{(k-1)}])$
  • 聚合函数AGG包括： 平均池化 / 逐维最大值 / LSTM
• Graph Isomorphism Network(GIN)
  • $h_v^{(k)}=f^{(k)}({\sum }_{u\in \mathcal{N}(v)}{h}_u^{(k-1)}+(1+{ϵ}^{(k)})h_v^{(k-1)})$

从局部到全局卷积

上面的方法阐述了如何用局部卷积更新每个点的特征值，如果我们走了相当多步数那么就能保证所有图上节点的信息都被传递了，那么我们能不能用一种更直接简单的方法来传递全局信息？答案是可以的，我们现在描述一种在神经网络背景下首次提出的方法，远早于GNN模型。

谱卷积

跟之前一样，我们讨论节点特征只有一维的情况。在选择任意节点次序后，我们可以把所有节点特征叠加一起，得到一个特征向量。

给定一个特征向量$x$和拉普拉斯矩阵$L$,能让我们在图$G$上量化$x$的平滑程度。

将$x$归一化后，计算瑞利商$R_L(x)=\frac{x^{T}Lx}{x^{T}x}=\frac{{\sum }_{(i,j)\in E}(x_i-x_j{)}^2}{{\sum }_i{x}_i^2}={\sum }_{(i,j)\in E}(x_i-x_j{)}^2$

我们可以看出赋予邻点值相似的特征向量$x$会有更小的瑞利商。

L是实值对称矩阵，意味着它总有特征值${\lambda }_1\le ...\le {\lambda }_n$。根据特征值的最小最大理论：

$argmi{n}_{x,x\perp \{u_1,...,u_{o-1}\}}{R}_L(x)=u_i,mi{n}_{x,x\perp \{u_1,...,u_{o-1}\}}{R}_L(x)={\lambda }_i$

$L$的特征值集合称为谱，我们定义$L$的光谱分解：$L=U\Lambda U^T$，$\Lambda$是特征值排序后的特征矩阵，$U$是特征向量的矩阵(按照增加的特征值排序) 。
A = [ λ 1 ⋱ λ n ] , U = [ u 1 ⋯ u n ] A=\begin{bmatrix}\lambda_1\\ & \ddots\\ & & \lambda_n\end{bmatrix} , U=\begin{bmatrix}u_1 \cdots u_n\end{bmatrix} A= ​λ1​​⋱​λn​​ ​,U=[u1​⋯un​​]
特征向量之间的正交性提供了$U^{T}U=I$，由于这n个特征向量都来自${\mathbb{R}}^n$,任意特征向量$x$可表示为这些特征向量的线性组合$x={\sum }_{i=1}^n\widehat{x_i}{u}_i=U\hat{x}$

由$x=U\hat{x}⟺U^{T}x=\hat{x}$，这允许我们对任意向量$x\in {\mathbb{R}}^n$在自然数表示和谱表示中切换。

自然图像的谱图表示

前面我们说过图像可表示成一种格状图（像素表示点，对相邻像素连边，根据其位置可以有3，5，8个邻居，每个点特征值可能是一维或三维向量，如果算上alpha通道会是四维）。这个构造能让我们计算图拉普拉斯$L$和特征向量矩阵$U$。为了揭示谱表示实际上编码，我们在图像的每个通道上独立地进行以下操作：

• 所有像素值转为一个特征向量矩阵$x$
• 获得谱表示$\hat{x}=U^{T}x$
• 定义谱成分数$m$为使用前$m$个特征向量组成的矩阵，后面的值转化为0。即${\hat{x}}_m=Truncat{e}_m(\hat{x})$
• 然后我们再传回自然表示$x_m=U\hat{x}$

我们将其还原成一个图像就能得到如下结果：

随着谱成分数m减少，图片会变得越加模糊，当降为1时仅有一种颜色。而通过减少m我们可以发现降低成分后仍能够保存很多信息，这可以跟图像上的傅里叶分解联系起来: 我们使用的特征向量越多，我们在网格上表示的频率就越高。下面是一个可视化的8*8图像，通过改变谱系数来查看图像变化。（可在原文进行互动）

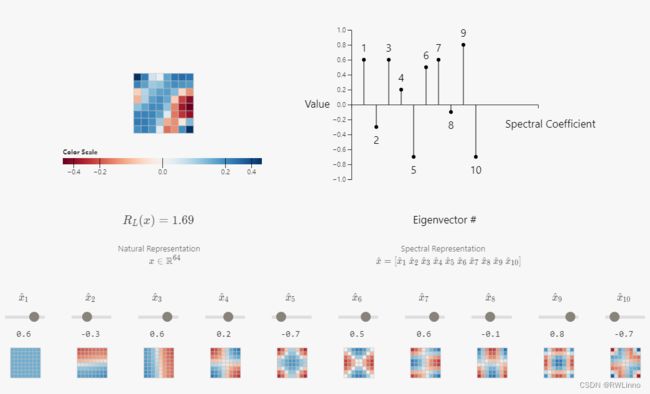
可直观看到第一个特征向量确实是光滑的，并且当我们考虑后面的特征向量时，光滑度相应地减小即可。对于任意图像$x$,为了捕捉全局性的图像趋势我们可以采用初始整体（高频成分）的谱表示，包括捕捉一些局部细节（低频成分）。

嵌入计算

我们现在已经有了理解谱卷积的背景，以及如何使用它们来计算节点的嵌入（特征）表示。

跟之前一样，我们将模型分为$k$层，每一层都有可学习参数${\hat{w}}^{(k)}$，称为过滤器权重。这些权重将与节点特征的谱表示相卷积。结果是每层权重所需参数的数量等于用于计算谱表示的特征向量数$m$。我们前面已提到可以去$m<<n$使得输入的重要信息不会丢失太多。因此，在谱域上的卷积比在自然域的直接卷积能够使用更少的参数。再者，由于图上拉普拉斯特征向量平滑的良好属性，使用谱表示自然而然就能对邻近节点施加感应偏差以获得相似的表示。

假设现在是一维的节点特征，每一层的输出是一个节点表示的向量$h^{(k)}$，其中每个点的表示对应向量中的一行。
h ( k ) = [ h 1 ( k ) ⋮ h n ( k ) ] , k = 0 , 1 , 2... , K h^{(k)} = \begin{bmatrix}h_1^{(k)}\\ \vdots \\h_n^{(k)}\end{bmatrix} , k=0,1,2...,K h(k)= ​h1(k)​⋮hn(k)​​ ​,k=0,1,2...,K
我们固定图$G$上节点的顺序以得到邻接矩阵$A$和拉普拉斯矩阵$L$，使得我们能够计算$U_m$。最后，我们可以按一下方式计算每层的结果：

• 初始特征值：$h^{(0)}=x$
• 迭代过程如下：$k=1,2,...,K$
  • 将前一层特征转化为谱表示：${\hat{h}}^{(k-1)}=U_m^T{h}^{(k-1)}$
  • 在谱域上进行卷积操作（w为可学习参数）：${\hat{g}}^{(k)}={\hat{w}}^{(k)}\odot {\hat{h}}^{(k-1)}$
  • 将结果转回自然域表示：$g^{(k)}=U_m{\hat{g}}^{(k)}$
  • 引入非线性项：$h^{(k-1)}=\sigma (g^{(k)})$

我们可以将图的谱域卷积看作是图的频域卷积的推广。（然后这跟快速傅里叶变换一样加快了计算过程）

谱卷积是节点顺序等效的

（证明跳过了）

谱卷积的理论在数学上是严谨的；然而我们仍需要讨论一些缺陷：

• 我们需要从$L$计算特征向量矩阵$U_m$，对于大型图来说不可行
• 即便计算了$U_m$,全局卷积也是不高效的，因为$U_m$和$U_m^T$的重复计算
• 所学习的滤波器是输入图特定的，因为他们是基于输入图拉普拉斯的表示，这意味着在很不一样的新图结构上很难做迁移学习

由于上述原因谱卷积已经在很大程度上被“局部”卷积所取代，但是理解它们背后的思想仍然有很多优点。事实上，最近提出的一种叫方向图网络的 GNN 模型使用拉普拉斯特征向量和他们的数学性质。

基于图嵌入的全局传播

一种简单的结合图级别信息的方式就是在我们迭代结构的过程中，通过池化节点（或边）嵌入来计算整个图的嵌入，并使用图嵌入去更新节点嵌入。一般图神经网络使用的是这种方法，然而这样似乎忽略了谱卷积能捕捉到的图底层拓扑结构。

学习GNN参数

我们在这里描述的所有嵌入计算你，不管是谱域还是空间上都是完全可微的，这允许 在损失函数$\mathcal{L}$合适的前提下GNN 以端到端的方式进行训练，就像标准的神经网络一样。

• 节点分类任务：通过通过最小化分类任务的任何标准损失，例如当存在多个类时的分类交叉熵。
  • 预测节点v在类c的概率：$\mathcal{L}(y_v,\widehat{y_v})=-{\sum }_c{y}_{vc}(log\widehat{y_{vc})}$
  • 定义整个图的损失${\mathcal{L}}_{\mathcal{G}}=\frac{{\sum }_{v\in Lab(G)}\mathcal{L}(y_v,\widehat{y_v})}{|Lab(G)|}$
• 图像分类：
• 链路预测：通过抽样相邻和非相邻节点对，并使用这些向量对作为输入来预测边的存在/不存在。举一个具体的例子，通过最小化以下类似“ Logit模型”的损失
  • $\mathcal{L}(y_v,y_u,e_{vu})=-e_{vu}log(p_{vu})-(1-e_{vu})log(1-p_{vu}),p_{vu}=\sigma (y_v^T{y}_u)$
• 点聚类：训练GNN预测局部或全局图属性/ 自监督技术使相邻节点获取类似的嵌入 / 模仿随机游走
  • $L_G={\sum }_v{\sum }_{u\in N_R(v)}log\frac{exp{z}_v^T{z}_u}{{\sum }_{u^{\prime }}exp{z}_{u^{\prime }}^T{z}_u}$,$N_R(v)$表示从v开始随机游走的多重点集。对于计算代价昂贵的大型图来说，像噪声对比估计这样的技术回很有用。