Python数值分析案例01--------四阶龙格库塔法解抛体运动

在考虑到空气阻力（）和因地球自转引起的科里奥利力后，列出运动方程

---->抛出点的北纬读数

---->表示地球自转角速度

算法:

四阶龙格库塔

代码

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
from math import *

def runge_kutta4(df,a,b,h,y0):
    num = len(y0)
    t = np.arange(a,b+h,h)
    w = np.zeros((t.size,num))
    w[0,:] = y0

    for i in range(t.size - 1):
        s0 = df(t[i], w[i,:])
        s1 = df(t[i] + h/2.,w[i,:] + h * s0 / 2.)
        s2 = df(t[i] + h/2.,w[i,:] + h * s1 / 2.)
        s3 = df(t[i+1], w[i,:] + h * s2)
        w[i+1,:] = w[i,:] + h * (s0 + 2*(s1+s2) + s3) / 6.

        if w[i+1,:][2] <= 0:
            q = i
            xl,yl,zl =  w[i+1,:][0],w[i+1,:][1],max(w[:,2])
            break
        
    return t,w,q,xl,yl,zl

def df(t, variables):
    x,y,z,x1,y1,z1 = variables
    
    A = np.zeros((3,3))
    b = np.zeros(3)
    
    A[0,0] = 1
    A[0,1] = 0
    A[0,2] = 0
    
    A[1,0] = 0
    A[1,1] = 1
    A[1,2] = 0

    A[2,0] = 0
    A[2,1] = 0
    A[2,2] = 1

    phi = 30 * pi/180
    k = 0.00001
    n = 5
    g = 9.8
    
    b[0] = -2 * pi * 15/180/3600 * (cos(phi) * z1 - sin(phi) * y1) - k * (x1)**n
    b[1] = -2 * pi * 15/180/3600 * sin(phi) * x1 - k * (y1)**n
    b[2] = -g + pi * 15/180/3600 * 2 * cos(phi) * x1 - k * (z1)**n
    
    x2,y2,z2 = np.linalg.solve(A, b)

    return np.array([x1,y1,z1,x2,y2,z2])

a,b = 0.0,20.0
h = 0.01

x = 0
y = 0
z = 0
x1 = 10 
y1 = 0
z1 = 70

y0 = np.array([x,y,z,x1,y1,z1])

t,w,q,xl,yl,zl = runge_kutta4(df, a, b, h, y0)

x = w[:,0]
y = w[:,1]
z = w[:,2]
x1 = w[:,3]
y1 = w[:,4]
z1 = w[:,5]

if 1:
    fig = plt.figure()
    ax = fig.add_subplot(projection='3d')
    ax.scatter(x,y,z,label="projectile",s=0.5)

    ax.set_xlabel("X"+" covers "+str(round(xl,2)) +" meters in x")
    ax.set_ylabel("Y"+" covers "+str(round(yl,2)) +"meters in y")
    ax.set_zlabel("Z"+" the highest is "+str(round(zl,2)) +" meters in z")
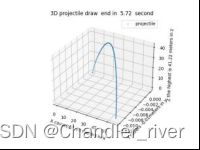
    ax.set_title("3D projectile draw"+"  end in  "+str(q*h)+"  second")
    
    ax.legend()
    
else:
    #plt.plot(x,z)
    plt.plot(x,y)
plt.show()

效果图

    Vx=10,Vy=10,Vz=20,k=0.000001,n=5

Vx,y=0.5Vz=10 ，k=0.05 n=2