算法刷题：动态规划-背包问题学习整理

---

前言

本篇记录笔者对于动态规划中的背包问题再次学习的整理

一、背包问题

定义

背包问题前置知识

滚动数组

所谓的滚动数组，就是在动态规划中，在同一个维度的空间上，新一层计算的结果覆盖上一层计算的结果，从而达到降维和节省空间的目的，具体大家可以参照以下这段话

有时某些二维dp方程可以直接降阶到一维，在某些题目中甚至可以降低时间复杂度，是一种极为巧妙的思想，简要来说就是通过观察dp方程来判断需要使用哪些数据，可以抛弃哪些数据， 一旦找到关系，就可以用新的数据不断覆盖旧的数据量来减少空间的使用

下面我们来看具体的例子

如：斐波那契数列，我们使用滚动数组对该问题的解法进行优化

• 正常斐波那契数列的写法

#include
using namespace std;
int main()
{
	int a[37];
	a[0]=1;
	a[1]=1;
	//求斐波那契数列第37个数
	for(int i=2;i<=36;i++){
		a[i]=a[i-1]+a[i-2];
	}
	printf("%d\n",a[36]);
	return 0;
} 

• 优化版斐波那契数列的写法
  我们注意到，实际上我们参与计算的过程中，只有三个数起到了作用，所以我们其实在用三个数进行变换，所以这里我们可以使用滚动数组进行简化

#include
using namespace std;
int main()
{
    int a[3];
    a[0] = 1;
    a[1] = 1;
    for(int i = 1;i <= 35;i++)
    {
        a[2] = a[0] + a[1];
        a[0] = a[1];
        a[1] = a[2];
    }
    printf("%d\n",a[2]); 
    return 0;
}

0-1背包问题

我们这里对0-1背包问题使用斐波那契数列数组进行简化，这一部分知识的阅读需要相关背包问题的储备知识，如果没有学习过背包问题的小朋友建议先行学习背包问题，再来查看这部分的讲解内容

二、背包问题分类及其解法

1.0-1背包问题

每件物品至多取一次，也就是说每件物品只有一个

0-1背包问题思路梳理和题解

0-1背包问题，无非是选与不选两种状态，可以选用二维数组f[i][j],表示涉及前i个物品，体积为j的情况下，0-1背包问题的最优解，其中选与不选，可通过当前位置选该物品和不选该物品进行比较，具体可查看笔记图片和代码

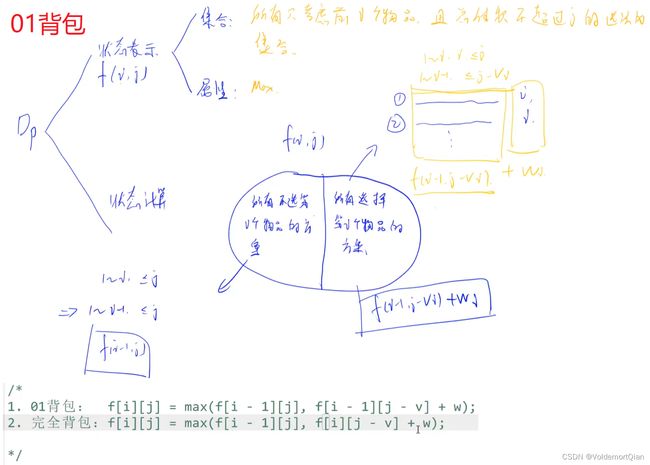
二维代码书写

#include

using namespace std;

const int N=1010;
int n,m;

int v[N];
int w[N];

int f[N][N];

int main(){
    
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
            f[i][j]=f[i-1][j];//i种物品下，体积为j的情况先取i-1种物品的情况下总价值
            if(j>=v[i]) f[i][j]=max(f[i][j],f[i-1][j-v[i]]+w[i]);//前者表示不选，后者表示当前选第i种物品，利用j进行了优化
        }
    }
    cout<<f[n][m]<<endl;
}

优化方案

0-1背包问题可直接从二维优化到一维

因为我们观察到，在i的遍历中，无论是选择第i种物品，使得价值变为

            f[i][j]=f[i-1][j];

还是不选第i种物品，使得价值变为

            f[i][j]=f[i-1][j-v[i]]+w[i];

我们都可以知道，在二维数组种，当前层是由上一层推演而来，所以这里，其实我们可以使用滚动数组，进行一维上的简化覆盖

#include

using namespace std;

const int N = 1010;
int n, m;
int v[N], w[N];
int f[N];

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> v[i] >> w[i];

    for (int i = 1; i <= n; i ++)
        for (int j = m; j >= v[i]; j -- ) // 01背包 一维写法 只能 逆序更新
        // 完全背包 一维写法 只能 正序更新：for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v[i]] + w[i]);

    cout << f[m] << endl;
    return 0;
}

同时我们观察到，因为是滚动数组，且每轮中第i次决策才会用到v[i]和w[i]，所以我们不妨进一步优化，在数据输入中直接进行处理，当然这其实局限于算法题的写法(会牺牲一定的代码可读性)

#include

using namespace std;

const int N = 1010;
int n, m;
int v, w;
int f[N];

int main(){
    cin >> n >> m;

    for (int i = 1; i <= n; i ++){ // 注意加了cin >> v >> w; 之后, 这里有个 大括号
        cin >> v >> w; // 注意 不是在 第二个 for循环里
        for (int j = m; j >= v; j -- ) // 01背包 一维写法 只能 逆序更新
        // 完全背包 一维写法 只能 正序更新：for (int j = v[i]; j <= m; j ++ )
            f[j] = max(f[j], f[j - v] + w);
    }

    cout << f[m] << endl;
    return 0;
}

2.完全背包问题

每件物品不设置数量，可以使用无限次

朴素写法

#include
using namespace std;
const int N=1010;
int n,m;
int f[N][N];
int w[N];
int v[N];

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
           for(int k=0;k*v[i]<=j;k++){
                f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
            } 
        }
            
    }    
    cout<<f[n][m]<<endl;
}

优化到二维：这里我们观察到

完全背包问题内部递推式子更新存在如下关系：

所以根据最后一个式子，可对最后一重K次循环进行优化到如下

#include
using namespace std;
const int N=1010;
int n,m;
int f[N][N];
int w[N];
int v[N];

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++){
        for(int j=0;j<=m;j++){
           f[i][j]=f[i-1][j];
           if(j>=v[i]) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    } 
    cout<<f[n][m]<<endl;
}

同时我们又观察到，f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);该式和0-1背包问题中的递推式子很相似，因而我们同样可以使用递推数组对该式进行优化，唯一不同的是0-1背包问题时候对使用到当前循环i的物品的更新方式是由上一轮循环的结果递归得到，但在多重背包问题中，对使用到当前循环i的物品的更新方式是由本轮循环中的结果得到，所以，完全背包问题控制背包容量的j是从本轮进行递增递推，这一点要和0-1背包问题进行区分；

因此采用滚动数组对完全背包问题优化得到的代码如下：

#include
using namespace std;
const int N=1010;
int n,m;
int f[N];
int w[N];
int v[N];

int main(){
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    
    for(int i=1;i<=n;i++){
        for(int j=v[i];j<=m;j++){
           f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    } 
    cout<<f[n][m]<<endl;
}

---

3.多重背包问题

每件物品设置了数量，例如设置了某件物品有Si个，你最多只能使用Si次

对于多重背包问题，我们设每件物品选中1，2，3，4，…一直到s个物品用完，有关系式如下

	f[i,j]=max(f[i-1,j],f[i-1,j-v]+w,f[i-1,j-2*v]+2*w,...,f[i-1,j-s*v]+s*w;

我们沿用完全背包问题的思路，查看是否能对其进行优化，得到的表达式是

我们可以看到，相比较完全背包问题，多重背包问题最后多出一项，我们可以这样理解多出的一项：在多重背包问题上方的式子中，限制s的最终数量是物品的实际数量，换句话说f[i-1,j-sv]+sw这里，最终是第i个物品用完，而下面f[i,j-v]也同样是第i个物品用完，所以多出一项

相关问题代码

#include 
#include 

using namespace std;

const int N = 12010, M = 2010;

int n, m;
int v[N], w[N];
int f[M];

int main(){
    cin>>n>>m;
    
    int cnt=0;//切割分组的坐标
    for (int i=1;i<=n;i++){
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;
        while (k<=s){
            cnt++;
            v[cnt]=a*k;
            w[cnt]=b*k;
            s-=k;
            k*=2;
        }
        if(s>0){
            cnt++;
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
    }//对多重背包进行二进制分组
    
    n=cnt;
    for (int i=1;i<=n;i++){
        for (int j=m;j>=v[i];j--){
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m];
    return 0;
}

4.分组背包问题

物品被分为若干组，每个组有若干个问题，通常为每组里面至多只能选一个

#include 
#include 

using namespace std;

const int N = 110;

int n, m;
int v[N][N], w[N][N], s[N];
int f[N];

int main()
{
    cin >> n >> m;

    for (int i = 1; i <= n; i ++ )
    {
        cin >> s[i];
        for (int j = 0; j < s[i]; j ++ )
            cin >> v[i][j] >> w[i][j];
    }

    for (int i = 1; i <= n; i ++ )
        for (int j = m; j >= 0; j -- )
            for (int k = 0; k < s[i]; k ++ )
                if (v[i][k] <= j)
                    f[j] = max(f[j], f[j - v[i][k]] + w[i][k]);

    cout << f[m] << endl;

    return 0;
}

参考博客

在此感谢以上博客答主，他们在我的学习阅读过程中给予了足够的思考帮助，衷心感谢

滚动数组及0-1背包问题优化方案