数据结构与算法(四)--队列
一、前言
前面的文章我们分别学习了线性结构中的数组和栈,这次我们学习另一种线性结构–队列。队列同栈,依然是把数据排成一排,且队列对应的操作依旧是数组的子集。但是队列只能从一端(队尾)添加元素,只能从另一端(队首)取出元素。
二、队列
我们前言说过,队列只能从一端(队尾)添加元素,只能从另一端(队首)取出元素。同这个数据结构的名字,它其实和我们日常生活中排队是非常相像的。例如:

增加元素就像排队一样,一次从队尾进入。如下图:
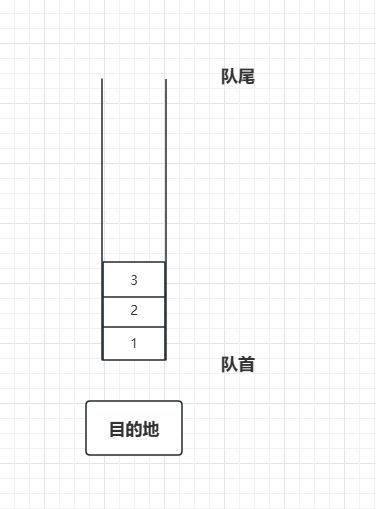
而从队列取出元素的时候,仍然和排队是一致的,从队首取出元素,如下图:

这一点和栈不同,栈的话取出的元素应该是3,而队列则是1.从上面我们可以分析出队列是一种先进先出的数据结构。英文也缩写我FIFO(Frist In First Out)
三、队列的实现
那么经过上次栈的实现,队列的实现就相对简单许多了,对于队列,我们需要实现以下方法:
void enqueue(E) //向队列添加元素(入队)E dequeue() //从队列取出元素(出队)E getFront() //查看队首元素int gitSize() //获取队列元素个数boolean isEmpty() //查看队列是否为空
同栈一样,用户无需关心队列的底层实现,所以我们写一个队列的接口,定义上述五个方法,然后写一个ArrayQueue通过我们之前实现的动态数组的方式实现这个队列。那么代码实现就很简单了,如下:
Queue接口类定义:
public interface Queue<T> {
void enqueue(T t);
T dequeue();
T getFront();
int getSize();
boolean isEmpty();
}
ArrayQueue类定义:
public class ArrayQueue<T> implements Queue<T> {
private DynamicArray<T> dynamicArray;
public ArrayQueue() {
this.dynamicArray = new DynamicArray<>();
}
public ArrayQueue(int size) {
this.dynamicArray = new DynamicArray<>(size);
}
@Override
public void enqueue(T t) {
dynamicArray.addLast(t);
}
@Override
public T dequeue() {
return dynamicArray.removeFirst();
}
@Override
public T getFront() {
return dynamicArray.getFirst();
}
@Override
public int getSize() {
return dynamicArray.gitSize();
}
@Override
public boolean isEmpty() {
return dynamicArray.isEmpty();
}
//这里为了查看方便,我将队列所有元素打印出来,同栈一样,用户一般只需关注队首的元素。
@Override
public String toString() {
return "ArrayQueue{" +
"Queue=" + dynamicArray.toString() +
'}';
}
}
然后测试一下:
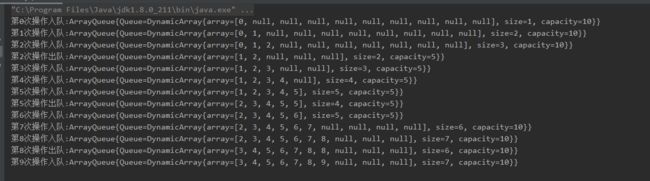
public static void main(String[] args) {
ArrayQueue<Integer> integerArrayQueue = new ArrayQueue<>();
for (int i = 0; i < 10; i++) {
integerArrayQueue.enqueue(i);
System.out.println("第" + i + "次操作入队:" + integerArrayQueue);
if (i % 3 == 2) {
integerArrayQueue.dequeue();
System.out.println("第" + i + "次操作出队:" + integerArrayQueue);
}
}
}
void enqueue(E) //向队列添加元素(入队) O(1)均摊E dequeue() //从队列取出元素(出队) O(n)E getFront() //查看队首元素 O(1)int gitSize() //获取队列元素个数 O(1)boolean isEmpty() //查看队列是否为空 O(1)
那么大家也能看到出队的时间复杂度为O(n),这样 依一来,如果队列元素非常非常多的时候,效率是非常慢的,例如队列100w个元素,此时如果执行出队,需要等待非常长的时间。那么我们后面就会介绍如何让我们队列做到**出队和入队均为O(1)**的复杂度–循环队列。
四、循环队列
删除队首元素
假设现在有如下队列,队列中共5个元素,容量为8:

由于取出队首元素后,其他元素都要往前挪一个位置,所以时间复杂度为O(n).
基于这样的分析,我们能不能得出这样的想法,当a这个队首元素被取出后,我们能不能不让b,c,d,e这些剩余的元素往前移动呢,如图:
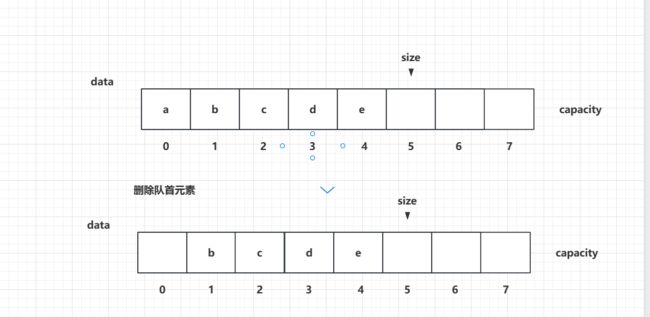
这样的话,a被取走后,剩余的元素仍然保持着队列的样子,b是队首,e是队尾。所以基于这样的想法,我们可以在数组中记录一下队首是谁,比如之前队首是a索引为0的位置,当a被取走后,虽然我们索引为0的空间是空着的,但是我们可以记一下队首front目前指向索引为1的位置,而我们定义一个属性为tail,它和size一样仍然指向下一个要插入元素的位置,和没取走a时是保持一致的:
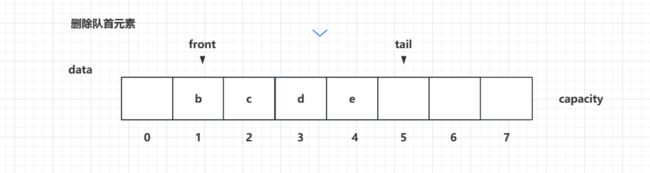
那么当我们取走队首元素的时候,我们只需维护下front的指向即可,而不需要每个元素向前移动一个单位。基于这样的思路,我们就有了循环队列这样的一种队列的实现方式。
需要注意的是:front == tail时,说明队列是空。
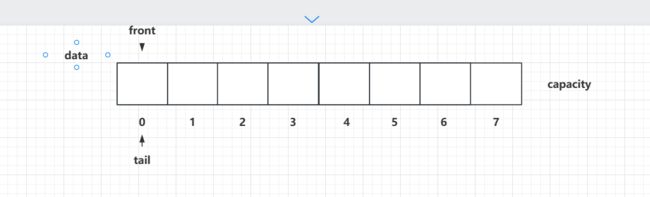
然后就是当放入元素时,tail++;取走元素时,front++.
那么你可能会有疑问,这个循环队列本身有什么关系呢,这就要说到当这个队列又有新的元素放进来的时候,直至这个队列被加满的情况:

假设现在元素被加满了,此时size已经不能往后++了,但是我们可以看到队首元素挪出我们的数组之后,这个空间没有被后面的元素给挤掉,那么对于我们的数组来说,前面有可能还有可以利用的空间,这就是循环队列的来由。我们可以把我们的数组看作一个环,现在一共能够容纳8个元素,对应索引是0-7,那么 7之后的索引其实是0,而不是直接说我们数据占满了。之前我们说的是tail++,其实应该是(当前索引+1)%(数组长度),例如7的下一个元素应该是(7+1)%8=0.所以新元素进来应该放在索引为0这个位置。然后tail++
索引上面的图应该改为:

添加元素后:
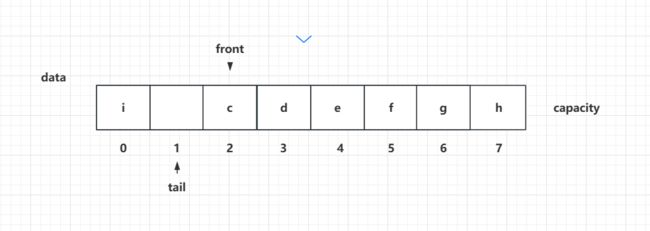
而当又有新的元素入队,此时有人会说索引=1的元素还是空的,是不是还可以把新的元素放在这儿。在这里就需要大家注意之前咱们聊到的一个条件:
front == tail时,说明队列是空
如果此时把新元素放在1这个位置,tail++=2=front,那么此时front=tail就不仅是象征队列为空,还代表这队列是满的,那这当然不是我们想看到的。所以我定义队列为满的定义应该是(tail + 1) %(数组长度) == front.此时我们就可以扩容了。
所以对于我们数组来说,我们其实是有意识的浪费一个空间。
然后就是数组内元素个数size的计算,我们当然可以从一开始记录一个size属性,然后对于相关操作同之前线性结构一样,对size做相对应的改变,但是对于循环队列来说,size我们可以凭front和tail这两个属性就可以计算出来。我们后续的代码实现也是不带有size的。
那么我们现在推一下这个size:
假设数据只进入队列,而不出队列,即front=0,在原处,而rear在不断增加。
此时显然,循环队列的元素个数为rear-front=rear-0 =rear, 如下图:tail=6且一共有6个元素

假设数据不进入队列,有出队列,如下图:
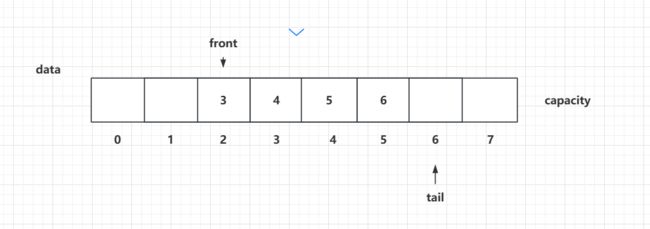
由上面可知,如果,数据只进入队列,而不出队列,则队列元素为rear,
那得到一个思路,就是旋转循环队列,让front=0,回到原处,rear不就是元素个数了吗
我们知道,如果说通过上面的例子,要让front到0,我只能同时出队入队
如果将数组想成一个环,想象一下,用顺时针旋转环;对于front要前进多少位置,我们可以得到以下公式:capacity-front = x;
此时front前进x格子就是(front + x) % capacity = (front + capacity -front) % capacity = 0;此时我们让front回到了0的位置。
而为了补齐这个数组,我的tail是不是也需要前进x格,此时tail = (tail + x)%capacity=(tail + capacity -front) % capacity。
所以我们得到size = (tail + capacity -front) % capacity
那么根据以上思路,我们可以有如下循环队列的实现:
在这里我们就不使用之前实现的动态数组实现,而是重新基于一个java的数组来实现。
public class LoopQueue<T> implements Queue<T> {
private T[] array;
private int front;
private int tail;
//客户自己设置的容量是希望我的队列能够承载的个数,
public LoopQueue(int capacity) {
array = (T[]) new Object[capacity + 1];
front = 0;
tail = 0;
}
public LoopQueue() {
this(10);
}
@Override
public void enqueue(T t) {
//当队列满时,需要扩容
if ((tail + 1) % array.length == front) {
resize(getCapacity() * 2);
}
array[tail] = t;
tail = (tail + 1) % array.length;
}
private void resize(int newCapacity) {
T[] newArray = (T[]) new Object[newCapacity + 1];
//记录下新的size,其实就是新数组的元素个数
int newSize = 0;
//然后就是将旧数组的元素从队首开始放入到新数组中,由于是循环数组,队首也可能不再是0,开始,而是front,且tail也有可能要比front小
// 所以i不再是单调的i++,而是(i + 1) % array.length
for (int i = front; i != tail; i = (i + 1) % array.length) {
//那么我新数组下标要从0开始,可以用逆时针思考一下,就是让front回到0,那么就是(i - front) % array.length
newArray[(i - front) % array.length] = array[i];
newSize ++;
}
array = newArray;
front = 0;
tail = newSize;
}
@Override
public T dequeue() {
if (isEmpty()) {
throw new IllegalArgumentException("can't dequeue from a empty queue");
}
T res = array[front];
array[front] = null;
front = (front + 1) % array.length;
//如果发现size=当前数组容量1/4,防止复杂度震荡,则将数组缩容至原来一半
if (getSize() == getCapacity() / 4 && getCapacity() / 2 != 0) {
resize(getCapacity() / 2);
}
return res;
}
@Override
public T getFront() {
if (isEmpty()) {
throw new IllegalArgumentException("queue is empty");
}
return array[front];
}
@Override
public int getSize() {
return (tail + array.length - front) % array.length;
}
@Override
public boolean isEmpty() {
return front == tail;
}
public int getCapacity() {
return array.length - 1;
}
@Override
public String toString() {
StringBuilder stringBuilder = new StringBuilder();
stringBuilder.append(String.format("Queue: size = %d, capacity = %d\n", getSize(), getCapacity()));
stringBuilder.append("front [");
for (int i = front; i != tail; i = (i + 1) % array.length) {
stringBuilder.append(array[i]);
if((i + 1) % array.length != tail){
stringBuilder.append(",");
}
}
stringBuilder.append("] tail, front = "+front + ", tail =" + tail+ ", array =" + Arrays.toString(array));
return stringBuilder.toString();
}
public static void main(String[] args) {
LoopQueue<Integer> integerLoopQueue = new LoopQueue<>();
for (int i = 0; i < 10; i++) {
integerLoopQueue.enqueue(i);
System.out.println("第" + i + "次操作入队:" + integerLoopQueue);
if (i % 3 == 2) {
integerLoopQueue.dequeue();
System.out.println("第" + i + "次操作出队:" + integerLoopQueue);
}
}
}
}
测试结果如下:

那么理解了循环队列如何成立的,我们就可以很轻松的完成leetcode622这道题目了,感兴趣的小伙伴可以自己实现一下。
我们现在来分析一下我们自己实现的循环队列的复杂度,以及用它和一开始的不循环的数组队列比较一下,看看有什么区别:
循环队列的复杂度分析:
void enqueue(E) //向队列添加元素(入队) O(1)均摊E dequeue() //从队列取出元素(出队) O(1)均摊E getFront() //查看队首元素 O(1)int gitSize() //获取队列元素个数 O(1)boolean isEmpty() //查看队列是否为空 O(1)
对比一下之前不循环的数组队列,我们可以看到出队操作从以前的O(n)变为O(1)均摊。其他仍然不变。
为了效果明显一点,我们写一个测试用例:用十万次入队和出队的操作来对比这两者的时间复杂度:
public class TestQueueCompare {
private static double testQueue(Queue<Integer> q,int opCount){
long startTime = System.currentTimeMillis();
Random random = new Random();
for (int i = 0; i < opCount; i++) {
q.enqueue(random.nextInt(Integer.MAX_VALUE));
}
for (int i = 0; i < opCount; i++) {
q.dequeue();
}
long endTime = System.currentTimeMillis();
return (endTime - startTime)/1000.0;
}
public static void main(String[] args) {
ArrayQueue<Integer> integerArrayQueue = new ArrayQueue<>();
LoopQueue<Integer> integerLoopQueue = new LoopQueue<>();
System.out.println("arrayQueue,time:"+testQueue(integerArrayQueue,100000)+"s");
System.out.println("loopQueue,time:"+testQueue(integerLoopQueue,100000)+"s");
}
}
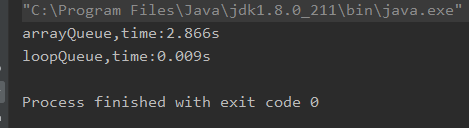
我们可以看到arrayQueue用了将近3s,而loopQueue用了0.01s不到。这样的差距就体现出来了,其实主要这个差距体现在出队上。对于ArrayQueue,出队是O(n),加之for循环整个方法复杂度已经来到了O(n^2).而对于循环队列,出队是O(1)均摊,加上for循环整个方法复杂度只是O(n)。n^2和n之间的区别在我这台电脑上区别就如上图测试达到了惊人的318倍左右。
这就是循环队列的意义,它的性能提升是非常明显的。
五、队列的应用
对于队列的应用,不管是业务层面例如排队还是说专业层面上的网络数据包排队,操作系统执行任务的排队都可以使用队列。队列本身就是一个很复杂的问题,对于队首本身它的定义是有很多方式的。也正因如此,存在广义队列这个概念,这个我们后续会学习。当然对于这一节实现的普通队列,在计算机领域也是有着重要应用的,例如广度优先遍历,这个呢我们后续学习二叉树的时候还会再次接触。