蓝桥杯集训·每日一题Week1

前缀和（Monday）

AcWing 3956. 截断数组（每日一题）

思路：

首先可以预处理出前缀和。判断数组长度如果小于 $3$ 或者前 $n$ 项不是 $3$ 的倍数，则可以直接输出 $0$。
否则就枚举所有 $s[i]=\frac{s[n]}{3}$，以及 $s[i]=\frac{2s[n]}{3}$ 的点，统计数量再相乘，最后输出即可。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/3/10 9:25
 */
public class Main {

    static final int N = 100010;
    static int[] s = new int[N];
    static int n;
    static long res;

    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer in = new StreamTokenizer(br);
    static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

    public static int nextInt() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    public static void main(String[] args) throws IOException {
        n = nextInt();
        for (int i = 1; i <= n; i++) {
            s[i] = nextInt();
            s[i] += s[i - 1];
        }

        int cnt = 0;
        if (n < 3 || s[n] % 3 != 0) {
            out.println(0);
        } else {
            for (int i = 2; i <= n - 1; i++) {
                if (s[i - 1] == s[n] / 3) cnt++;
                if (s[i] == s[n] * 2 / 3) res += cnt;
            }
            out.println(res);
        }
        out.flush();
    }

}

AcWing 795. 前缀和

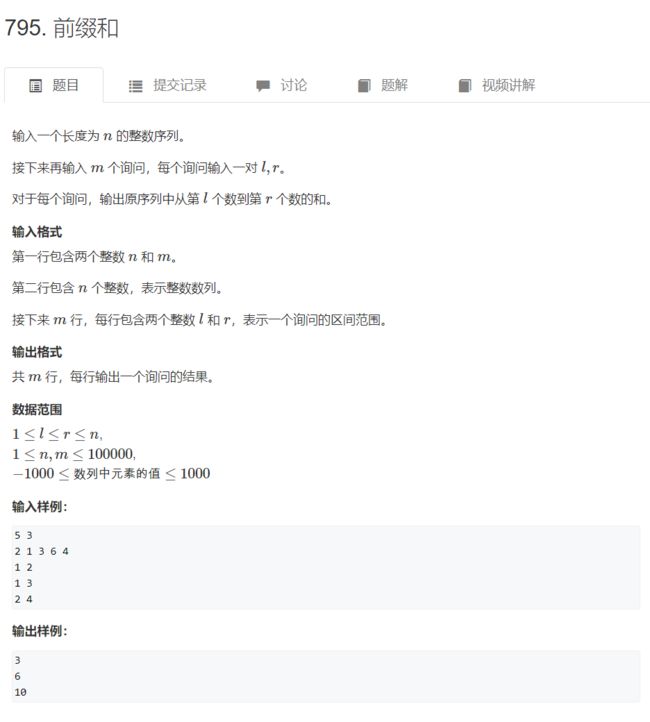
思路：
前缀和以 $O(1)$ 的复杂度求出一段区间的和。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 9:10
 */
public class Main {
    static final int N = 100005;
    static int n, m;
    static int[] a = new int[N], s = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        String[] nm = in.readLine().split(" ");
        n = Integer.parseInt(nm[0]);
        m = Integer.parseInt(nm[1]);

        String[] arr = in.readLine().split(" ");
        for (int i = 1; i <= n; i++) {
            a[i] = Integer.parseInt(arr[i - 1]);
            s[i] = a[i] + s[i - 1];
        }

        while (m-- != 0) {
            int l, r;
            String[] lr = in.readLine().split(" ");
            l = Integer.parseInt(lr[0]);
            r = Integer.parseInt(lr[1]);
            out.println(s[r] - s[l - 1]);
        }
        out.flush();
    }
}

AcWing 796. 子矩阵的和

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 9:22
 */
public class Main {
    static final int N = 1005;
    static int n, m, q;
    static int[][] s = new int[N][N];
    
    public static void main(String[] args) throws IOException {

        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        String[] nm = in.readLine().split(" ");
        n = Integer.parseInt(nm[0]);
        m = Integer.parseInt(nm[1]);
        q = Integer.parseInt(nm[2]);
        
        for (int i = 1; i <= n; i++) {
            String[] sub = in.readLine().split(" ");
            for (int j = 1; j <= m; j++) {
                s[i][j] = Integer.parseInt(sub[j - 1]);
            }
        }
        
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= m; j++) {
                s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
            }
        }
        
        while (q-- != 0) {
            int x1, y1, x2, y2;
            String[] idx = in.readLine().split(" ");
            x1 = Integer.parseInt(idx[0]);
            y1 = Integer.parseInt(idx[1]);
            x2 = Integer.parseInt(idx[2]);
            y2 = Integer.parseInt(idx[3]);
            out.println(s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]);
        }
        out.flush();
    }
}

AcWing 99. 激光炸弹

思路：

典型的子矩阵的和的问题，首先对输入的 $R$ 的范围进行限制，$R=min(R,5001)$，接着初始化子矩阵的和。接着枚举在 $R\times R$ 的范围内，价值的最大值。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 11:29
 */
public class Main {
    static final int N = 5002;
    static int[][] s = new int[N][N];
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        String[] nr = in.readLine().split(" ");
        int n = Integer.parseInt(nr[0]), r = Integer.parseInt(nr[1]);
        r = Math.min(5001, r);

        for (int i = 1; i <= n; i++) {
            String[] t = in.readLine().split(" ");
            int x = Integer.parseInt(t[0]), y = Integer.parseInt(t[1]), w = Integer.parseInt(t[2]);
            s[x + 1][y + 1] += w;
        }

        for (int i = 1; i <= 5001; i++) {
            for (int j = 1; j <= 5001; j++) {
                s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];
            }
        }

        int max = 0;

        for (int i = r; i < N; i++) {
            for (int j = r; j < N; j++) {
                max = Math.max(s[i][j] - s[i - r][j] - s[i][j - r] + s[i - r][j - r], max);
            }
        }
        out.println(max);
        out.flush();
    }
}

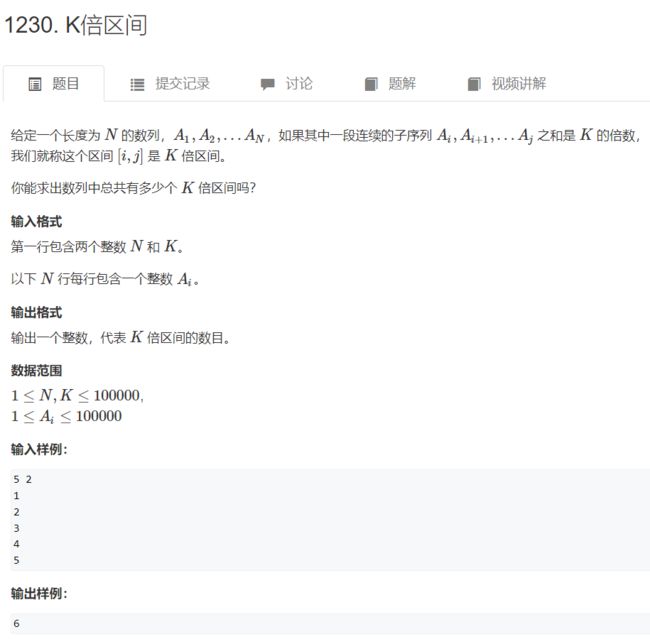
AcWing 1230. K倍区间

思路：

暴力做即使加上前缀和的优化也需要 $O(N^2)$ 的时间复杂度，在本题的规模下要超时，因此需要独辟蹊径。

容易想到，如果两个数模 $n$ 同余，那么这两个数的差值是 $n$ 的倍数。所以可以记录前缀和模 $k$ 的余数，计算余数相同的前缀和的个数，任选两个前缀和的差值即为 $k$ 的倍数，这样只用 $O(N)$ 的时间复杂度就可以计算出 $K$ 倍区间的数目。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 11:04
 */
public class Main {
    static final int N = 100005;
    static int[] s = new int[N];
    static int[] mod = new int[N];
    static long ans;
    static int n, k;
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        String[] nk = in.readLine().split(" ");
        n = Integer.parseInt(nk[0]);
        k = Integer.parseInt(nk[1]);

		// 余数为0先赋值为1，当区间和为前缀和时，需要用到
        mod[0] = 1;
        for (int i = 1; i <= n; i++) {
            s[i] = Integer.parseInt(in.readLine().split(" ")[0]);
            s[i] += s[i - 1];
            s[i] %= k;
            mod[s[i]]++;
        }

        for (int i = 0; i <= k - 1; i++) {
            ans += (long) mod[i] * (mod[i] - 1) / 2;
        }
        out.println(ans);
        out.flush();
    }
}

差分（Tuesday）

AcWing 3729. 改变数组元素（每日一题）

思路：

分析只，只要执行一次操作 $2$，数组元素都会变为 $1$，所以可以用差分构造每个数的操作 $2$ 的次数，如果大于 $1$，该数就为 $1$ 。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.Arrays;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/28 14:21
 */
public class Main {

    static final int N = 200005;
    static int t, n;
    // b记录操作的次数
    static int[] b = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        String T = in.readLine().split(" ")[0];
        t = Integer.parseInt(T);

        while (t-- != 0) {
            
            Arrays.fill(b, 0);
            String s = in.readLine().split(" ")[0];
            n = Integer.parseInt(s);
            String[] arr = in.readLine().split(" ");
            int x;
            for (int i = 1; i <= n; i++) {
                x = Integer.parseInt(arr[i - 1]);
                if (x == 0) continue;
                else if (x <= i) {
                    insert(i - x + 1, i, 1);
                }
                else insert(1, i, 1);
            }
            
            for (int i = 1; i <= n; i++) {
                b[i] += b[i - 1];
                out.print((b[i] > 0 ? 1 : 0) + " ");
            }
            out.println();
            out.flush();

            
        }
    }

    public static void insert(int l, int r, int c) {
        b[l] += c;
        b[r + 1] -= c;
    }
}

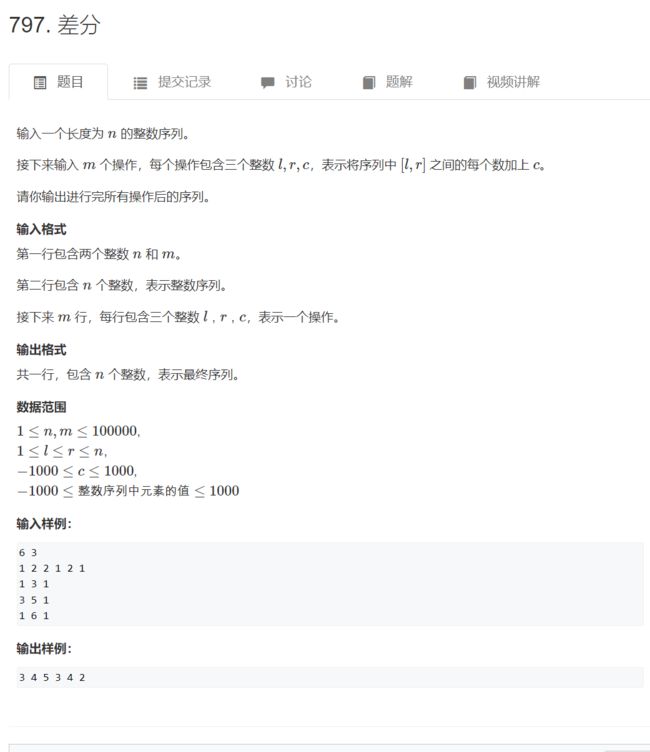
AcWing 797. 差分

给区间[l, r]中的每个数加上c：B[l] += c, B[r + 1] -= c

#include
using namespace std;

const int N = 1e6 + 5;
int a[N], q[N];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}
int main()
{
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++)
        scanf("%d", &a[i]);
    //构造差分数组b
    for (int i = 1; i <= n; i++)
        insert(i, i, a[i]);
    while (m --)
    {
        int l, r, c;
        scanf("%d%d%d", &l, &r, &c);
        insert(l, r, c);
    }
    for (int i = 1; i <= n; i++)
        b[i] += b[i - 1];
    for (int i = 1; i <= n; i++)
        printf("%d ", b[i]);
    return 0;
}

AcWing 798. 差分矩阵

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

#include
using namespace std;
const int N = 100010;
int n, m, q;
int a[N][N], b[N][N];
void insert(int x1, int y1, int x2, int y2, int c)
{
    b[x1][y1] += c;
    b[x2][y1 + 1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}
int main()
{
    cin >> n >> m >> q;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            cin >> a[i][j];
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            insert(i, j, i, j, a[i][j]);
    while (q--)
    {
        int x1, y1, x2, y2, c;
        cin >> x1 >> y1 >> x2 >> y2 >> c;
        insert(x1, y1, x2, y2, c);
    }
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= m; j++)
            b[i][j] += b[i][j - 1] + b[i - 1][j] - b[i - 1][j - 1];
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cout << b[i][j] << ' ';
        }
        cout << endl;
    }
    return 0;    
}

二分（Wednesday）

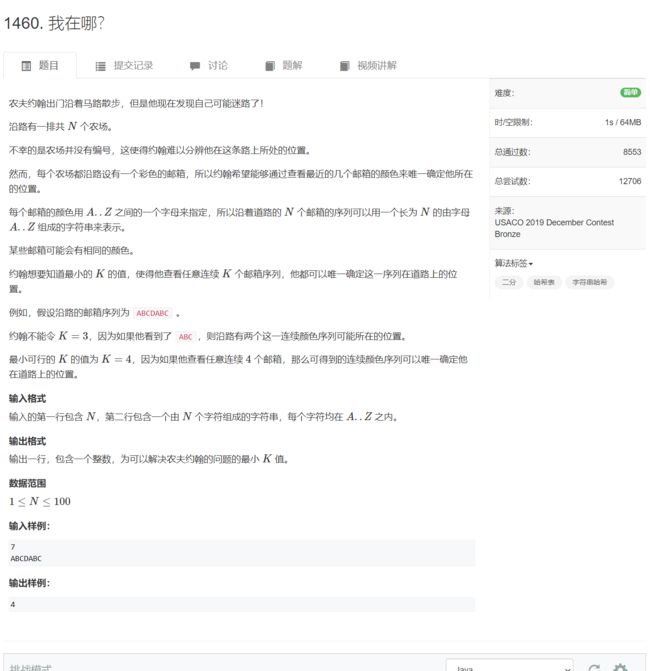
AcWing 1460. 我在哪？（每日一题）

思路：

本质上是一个寻找最短的不重复子串的问题，可以二分枚举子串的长度。构造子串可以用字符串哈希或者 substring(int fromIndex, int toIndex) 方法，数据范围大的话，建议用字符串哈希。

二分 + 字符串哈希：

核心思想： 将字符串看成P进制数，P的经验值是131或13331，取这两个值的冲突概率低
小技巧： 取模的数用 $2^{64}$，这样直接用 unsigned long long存储，溢出的结果就是取模的结果
注意： 字符串从 $1$ 的位置开始存。前 $l$ 位字符串的哈希值是 $h[l]$，前 $r$ 位字符串的哈希值是 $h[r]$，则 $l\sim r$ 之间字符串（包含端点）的哈希值可以表示为：
$$\begin{array}{rl}h[l\sim r]& =h[1\sim r]-h[1\sim l-1]\ast P^{r-l+1}\end{array}$$

模板

typedef unsigned long long ull;
ull h[N], p[N]; // h[k]存储字符串前k个字母的哈希值, p[k]存储 P^k mod 2^64

// 初始化
p[0] = 1;
for (int i = 1; i <= n; i ++ )
{
    h[i] = h[i - 1] * P + str[i];
    p[i] = p[i - 1] * P;
}

// 计算子串 str[l ~ r] 的哈希值
ull get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

#include 
#include 
using namespace std;

typedef unsigned long long ull;

const int N = 105, P = 131;
ull h[N], p[N];
char str[N];
int n;
set<ull> res;

ull get(int l, int r)
{
    return h[r] - h[l - 1] * p[r - l + 1];
}

bool check(int mid) 
{
    res.clear();
    for (int i = 1; i + mid - 1 <= n; i++)
    {
        ull t = get(i, i + mid - 1);
        if (res.find(t) != res.end()) return false;
        res.insert(t);
    }
    
    return true;
}

int main()
{
    cin >> n;
    cin >> str + 1;
    
    p[0] = 1;
    
    for (int i = 1; i <= n; i++) 
    {
        p[i] = p[i - 1] * P;
        h[i] = h[i - 1] * P + str[i];
    }
    
    int l = 1, r = 101;
    
    // 此模板用于求最小方案
    while (l < r)
    {
        int mid = l + r >> 1;
        if (check(mid)) r = mid;
        else l = mid + 1;
    }
    
    cout << l << endl;
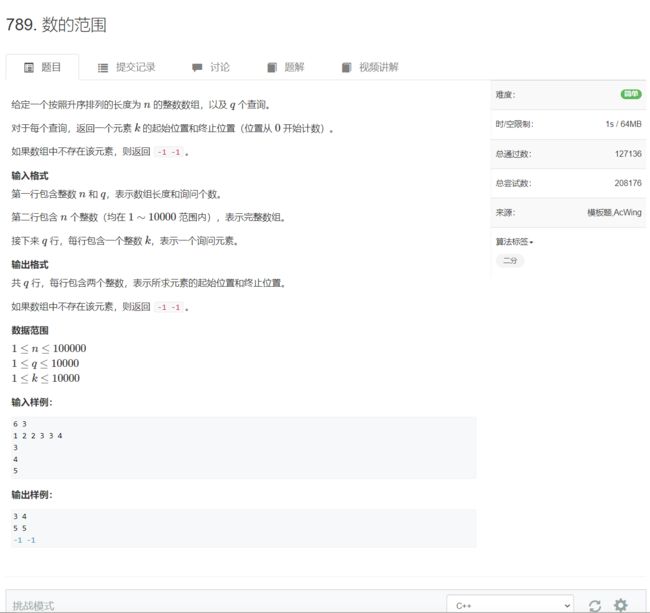
    return 0;
}

AcWing 789. 数的范围

思路：

二分模板一共有两个，分别适用于不同情况。
算法思路：假设目标值在闭区间[l, r]中， 每次将区间长度缩小一半，当l = r时，我们就找到了目标值。

版本1
当我们将区间[l, r]划分成[l, mid]和[mid + 1, r]时，其更新操作是r = mid或者l = mid + 1;，计算mid时不需要加1。

版本2
当我们将区间[l, r]划分成[l, mid - 1]和[mid, r]时，其更新操作是r = mid - 1或者l = mid;，此时为了防止死循环，计算mid时需要加1。

二分查找时，如果满足当前的 check() 函数，则继续二分。当查找数的左边界时，check() 函数 为 a[mid] >= x，满足条件时，需要更新右边界，r = mid，否则更新左边界 l = mid + 1，此时将区间[l, r]划分成[l, mid]和[mid + 1, r]，用的是第一版本的二分， mid = l + r >> 1。

当查找数的右边界时，check() 函数 为 a[mid] <= x，满足条件时，需要更新左边界，l = mid，否则更新右边界 r = mid - 1，此时将区间[l, r]划分成[l, mid - 1]和[mid, r]，用的是第二版本的二分，mid = l + r + 1 >> 1。

如果第一轮二分的结果，a[l] != x || a[r] != x，则不存在 x，此时输出 -1 - 1 即可。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 8:05
 */
public class Main {
    static final int N = 100005;
    static int[] a = new int[N];
    static int n, q, k;

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        String[] s = in.readLine().split(" ");
        n = Integer.parseInt(s[0]);
        q = Integer.parseInt(s[1]);

        String[] arr = in.readLine().split(" ");
        for (int i = 0; i < n; i++) a[i] = Integer.parseInt(arr[i]);

        while (q-- != 0) {
            int x = Integer.parseInt(in.readLine());
            int l = 0, r = n - 1;

            while (l < r) {
                int mid = l + r >> 1;
                if (a[mid] >= x) r = mid;
                else l = mid + 1;
            }

            if (a[l] != x) out.println("-1 -1");
            else {
                out.print(l + " ");
                l = 0;
                r = n - 1;

                while (l < r) {
                    int mid = l + r + 1 >> 1;
                    if (a[mid] <= x) l = mid;
                    else r = mid - 1;
                }

                out.print(r + "\n");
            }
        }
        out.flush();
    }
}

另外，使用 BufferedReader 与 PrintWriter 替换 Scanner 与 System.out.println()输入输出后，性能有了较大的飞跃。

AcWing 790. 数的三次方根

思路：

浮点数二分，最后的精度要求要比给定的要再精确两位。比如结果要求6位小数，则 eps = 1e-8。更新左右边界是将 mid 的值赋值给左右边界，当左右边界的差值小于 精度 eps 时，就结束二分。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 9:02
 */
public class Main {
    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));
        double n = Double.parseDouble(in.readLine());
        double eps = 1e-8;
        double l = -10000, r = 10000;

        while (r - l > eps) {
            double mid = (l + r) / 2;
            if (mid * mid * mid >= n) r = mid;
            else l = mid;
        }

        out.printf("%.6f", l);
        out.flush();
    }
}

AcWing 1227. 分巧克力

思路：

二分枚举边长的最大值，如果当前边长满足条件，更新左边界 l = mid，否则更新右边界 r = mid - 1，用的是第二个二分模板。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/25 10:14
 */
public class Main {
    static final int N = 100005;
    static int[] h = new int[N], w = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        String[] nk = in.readLine().split(" ");
        int n = Integer.parseInt(nk[0]);
        int k = Integer.parseInt(nk[1]);
        int sq = 0;

        for (int i = 0; i < n; i++) {
            String[] s = in.readLine().split(" ");
            h[i] = Integer.parseInt(s[0]);
            w[i] = Integer.parseInt(s[1]);
        }

        int ans = 0;

        int l = 1, r = 100001;

        while (l < r) {
            long num = 0;
            int mid = l + r + 1>> 1;
            for (int i = 0; i < n; i++) {
                num += (long)h[i] / mid * (w[i] / mid);
            }
            if (num >= k) {
                l = mid;
            }
            else r = mid - 1;
        }

        out.println(l);
        out.flush();
    }
}

双指针（Thursday）

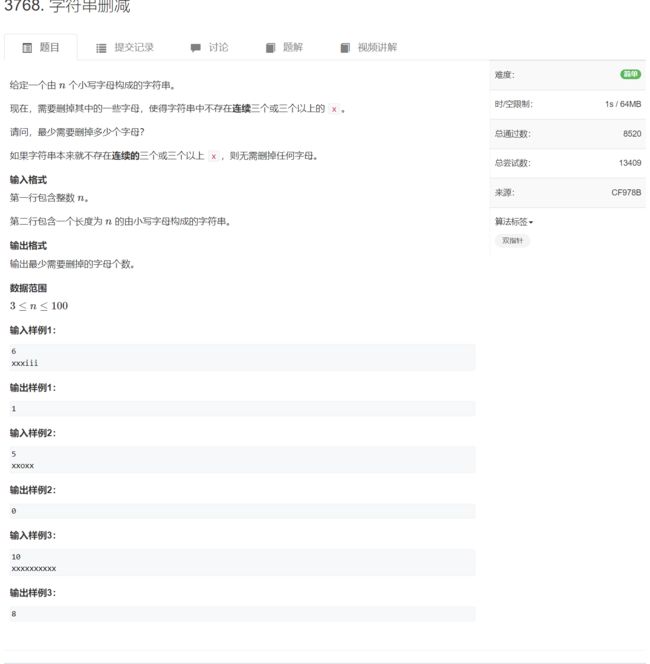
AcWing 3768. 字符串删减（每日一题）

思路：

双指针 $i$，$j$ 分别记录连续的 $x...$ 子串的开始与结尾，统计重复字串的长度，减到长度为 $2$ 即可，不够 $3$ 可以不用减。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/3/3 14:01
 */
public class Main {
    public static void main(String[] args) throws IOException{
        BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
        PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

        int n = Integer.parseInt(in.readLine());
        String s = in.readLine();

        int ans = 0;
        for (int i = 0; i < n; i++) {
            
            // 求连续的x的长度
            if (s.charAt(i) == 'x') {
                int j = i + 1;
                while (j < n && s.charAt(j) == 'x') j++;
                ans += Math.max(j - i - 2, 0);
                i = j;
            }
        }

        out.println(ans);
        out.flush();
    }
}

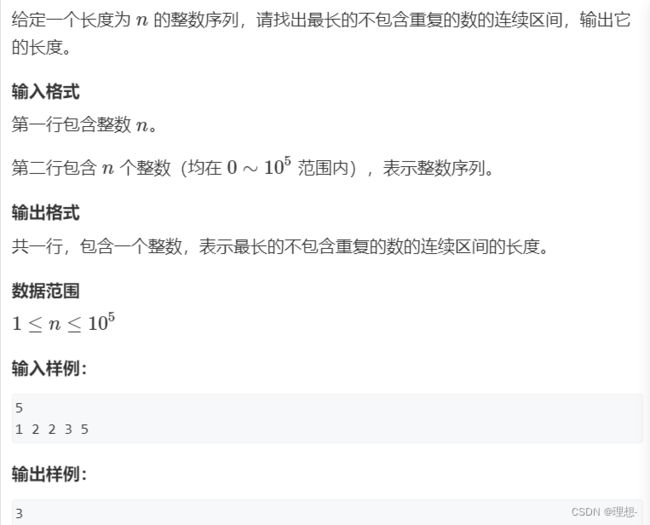
AcWing 799. 最长连续不重复子序列

#include 
using namespace std;

const int N = 100005;
int cnt[N], a[N];
int n;

int main()
{
    cin >> n;
    int res = 0;
    for (int i = 0; i < n; i++) cin >> a[i];
    for (int i = 0, j = 0; i < n; i++)
    {
        // i为终点，j为起点
        cnt[a[i]]++;
        // 遇到重复的元素 j往后移 同时重复的元素的个数-1
        while (cnt[a[i]] > 1) cnt[a[j++]]--;
        // 枚举从起点到终点的距离的最大值
        res = max(res, i - j + 1);
    }
    cout << res;
    return 0;
}

AcWing 800. 数组元素的目标和

#include 
using namespace std;
const int N = 100005;
int a[N], b[N];

int main()
{
    int n, m, x;
    cin >> n >> m >> x;
    for (int i = 0; i < n; i++) cin >> a[i];
    for (int j = 0; j < m; j++) cin >> b[j];
    
    int i = 0, j = m - 1;
    //从两端枚举
    while (i < n && j >= 0)
    {
        // 和大于x, j向前移动
        while (a[i] + b[j] > x) j--;
        // 和小于x, i向后移动
        while (a[i] + b[j] < x) i++;
        if (a[i] + b[j] == x) 
        {
            cout << i << ' ' << j;
            break;
        }
    }
    
    return 0;
}

递推（Friday）

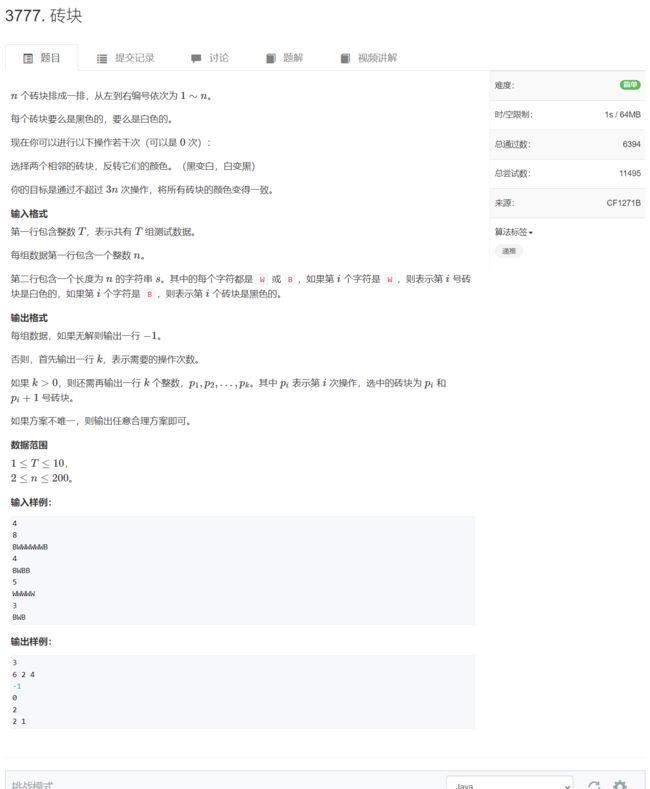
AcWing 3777. 砖块（每日一题）

思路：

首先，如果两种颜色的砖块都是奇数个数，则无法通过翻转变成同一种颜色，如果只有一种颜色，则不用翻转。

可以分两种情况。

• 都翻转成白色。遇到黑的就翻转，最后判断最后一个砖块是不是白色
• 都翻转成黑色。遇到白的就翻转，最后判断最后一个砖块是不是黑色

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/3/6 9:18
 */
public class Main {

    static int T, n;

    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer in = new StreamTokenizer(br);
    static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));

    public static int nextInt() throws IOException {
        in.nextToken();
        return (int) in.nval;
    }

    public static void main(String[] args) throws IOException {
        T = nextInt();

        while (T-- != 0) {
            n = nextInt();
            int a = 0, b = 0;
            int[] p1 = new int[205];
            int[] p2 = new int[205];
            int[] d1 = new int[205];
            int[] d2 = new int[205];
            int cnt1 = 0, cnt2 = 0;
            String s = br.readLine();
            // 0白 1黑
            for (int i = 0; i < n; i++) {
                if (s.charAt(i) == 'W') {
                    d1[i] = 0;
                    d2[i] = 0;
                    a++;
                } else {
                    d1[i] = 1;
                    d2[i] = 1;
                    b++;
                }
            }

            if (a % 2 == 1 && b % 2 == 1) out.println(-1);
            else if (a == 0 || b == 0) out.println(0);
            else {
                for (int i = 0; i < n - 1; i++) {
                    // 都换成白的
                    if (d1[i] == 1) {
                        d1[i] = 0;
                        d1[i + 1] = 1 - d1[i + 1];
                        p1[cnt1++] = i + 1;
                    }
                }

                for (int i = 0; i < n - 1; i++) {
                    // 都换成黑的
                    if (d2[i] == 0) {
                        d2[i] = 1;
                        d2[i + 1] = 1 - d2[i + 1];
                        p2[cnt2++] = i + 1;
                    }
                }

                if (d1[n - 1] != 0) {
                    out.println(cnt2);
                    for (int i = 0; i < cnt2; i++) out.printf("%d ", p2[i]);
                    out.println();
                } else {
                    out.println(cnt1);
                    for (int i = 0; i < cnt1; i++) out.printf("%d ", p1[i]);
                    out.println();
                }
            }
        }
        out.flush();
    }
}

AcWing 95. 费解的开关

思路：

考虑第一行，有 $2^n$ 种不同的状态。对于第一行的每个灯的状态，由于每个开关状态的改变会影响上下左右的所有开关的状态，所以在第一行，如果某灯是灭的话，有且仅有该灯下面第二行的开关的改变能影响该灯的状态，也就是说，只有正下方的开关可以改变上一层的状态，第 $n$ 行 确定 $n+1$ 行的状态，第一行确定整个的状态，所以只需要用二进制枚举第一行的状态即可，判断最后一行是否都为亮的，如果都是亮的，则有可行解，再判断可行解与 6 的 关系。

为保证不同的操作方式之间的结果不干扰，一开始要对原始数组先备份，然后再还原。

代码：

import java.util.Arrays;
import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/23 15:46
 */
public class Main {

    static final int N = 6;
    static char[][] g = new char[N][N], backup = new char[N][N];
    static int n;

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        n = scanner.nextInt();

        while (n-- != 0) {

            for (int i = 0; i < 5; i++) {
                String s = scanner.next();
                g[i] = s.toCharArray();
            }

            int res = 10;


            for (int op = 0; op < (1 << 5); op++) {

                for (int j = 0; j < 5; j++) {
                    backup[j] = Arrays.copyOf(g[j], 5);
                }

                int step = 0;

                for (int i = 0; i < 5; i++) {
                    if ((op >> i & 1) == 1) {
                        step++;
                        turn(0, i);
                    }
                }

                for (int i = 0; i < 4; i++) {
                    for (int j = 0; j < 5; j++) {
                        if (g[i][j] == '0') {
                            step++;
                            turn(i + 1, j);
                        }
                    }
                }
                boolean flag = false;

                for (int i = 0; i < 5; i++) {
                    if (g[4][i] == '0') {
                        flag = true;
                        break;
                    }
                }

                if (!flag) res = Math.min(res, step);
                for (int j = 0; j < 5; j++) {
                    g[j] = Arrays.copyOf(backup[j], 5);
                }

            }

            if (res > 6) System.out.println(-1);
            else System.out.println(res);
        }

    }


    public static void turn(int x, int y) {
        int[] dx = {-1, 1, 0, 0, 0}, dy = {0, 0, -1, 1, 0};

        for (int i = 0; i < 5; i++) {
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= 5 || b < 0 || b >= 5) continue;
            g[a][b] ^= 1;
        }
    }
}

AcWing 116. 飞行员兄弟

思路：

因为本题规模不大，所以可以通过枚举和位运算来求解，一共有 16 个位置，则有 $2^{16}=65536$ 种状态，最后判断开关的状态。用ArrayList 来存储操作，仅当操作数更少的时候，才更新操作集。

代码：

import java.util.ArrayList;
import java.util.Arrays;
import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/23 16:48
 */
public class Main {
    static final int N = 5;
    static char[][] g = new char[N][N], backup = new char[N][N];

    static class Node {
        int x, y;

        Node(int x, int y) {
            this.x = x;
            this.y = y;
        }
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        ArrayList<Node> ans = new ArrayList<>();
        for (int i = 0; i < 4; i++) {
            String s = scanner.next();
            g[i] = s.toCharArray();
        }

        for (int op = 0; op < (1 << 16); op++) {

            for (int j = 0; j < 4; j++) {
                backup[j] = Arrays.copyOf(g[j], g[j].length);
            }

            ArrayList<Node> tmp = new ArrayList<>();


            for (int i = 0; i < 4; i++) {
                for (int j = 0; j < 4; j++) {
                    if (((op >> (i * 4 + j)) & 1) == 1) {
                        turn(i, j);
                        tmp.add(new Node(i, j));
                    }
                }
            }

            boolean flag = false;
            for (int i = 0; i < 4; i++) {
                for (int j = 0; j < 4; j++) {
                    if (g[i][j] == '+') {
                        flag = true;
                        break;
                    }
                }
            }

            if (!flag) {
                if (ans.isEmpty() || ans.size() > tmp.size()) ans = tmp;
            }

            for (int j = 0; j < 4; j++) {
                g[j] = Arrays.copyOf(backup[j], backup[j].length);
            }

        }

        System.out.println(ans.size());
        for (Node tmp : ans) {
            System.out.println((tmp.x + 1) + " " + (tmp.y + 1));
        }

    }

    public static void turn(int x, int y) {
        for (int i = 0; i < 4; i++) {
            g[x][i] = g[x][i] == '+' ? '-' : '+';
            g[i][y] = g[i][y] == '+' ? '-' : '+';
        }
        g[x][y] = g[x][y] == '+' ? '-' : '+';

    }
}

AcWing 1208. 翻硬币

思路：

本题有不超过100个元素，枚举状态会超时，可以考虑贪心来做，如果两个字符串某个相同位置的元素不相同，就翻转，操作的次数就加一。这样只需要用到 $O(N)$ 的时间复杂度。

代码：

import java.util.Scanner;

/**
 * @Description
 * @Author: PrinceHan
 * @CreateTime: 2023/2/24 9:54
 */
public class Main {
    static final int N = 105;
    static char[] s1 = new char[N], s2 = new char[N];
    static String start, end;
    static int n, ans;
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        start = scanner.next();
        end = scanner.next();
        n = start.length();
        s1 = start.toCharArray();
        s2 = end.toCharArray();

        for (int i = 0; i < n - 1; i++) {
            if (s1[i] != s2[i]) {
                ans++;
                turn(i);
            }
        }

        System.out.println(ans);

    }

    public static void turn(int u) {
        s1[u] = s1[u] == '*' ? 'o' : '*';
        s1[u + 1] = s1[u + 1] == '*' ? 'o' : '*';
    }
}