C++初阶:stack&queue
stack&queue
1. 介绍
1.1 stack
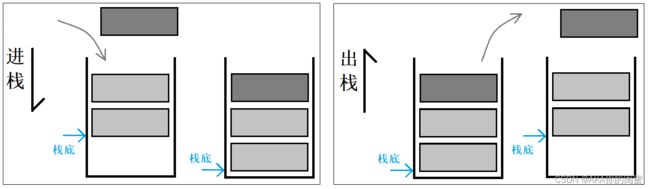
栈是一种特殊的线性表,只允许固定一端进行插入和删除。
能够插入删除的一端被称为栈顶,另一端被称为栈底。栈的元素遵循后进先出的原则。
栈的插入被称为压栈、进栈、入栈,删除被称为出栈、弹栈。
后进先出,先进后出, L I F O LIFO LIFO 原则(Last In First Out)。
1.2 queue
队列同样是一种特殊的线性表,和栈相反,队列只允许在其一端进行插入而在另一端进行删除。
插入数据的一端被称为队尾,删除的另一端被称为队头。队列的元素遵循先进先出的原则。
入队列就是队尾插入数据,出队列就是队头删除数据。
先进先出,后进后出,即 F I F O FIFO FIFO 原则(First In First Out)。
2. 接口
2.1 stack
STL中的栈和队列不是容器而是容器适配器。
template <class T, class Container = deque<T> >
class stack;
stack 的底层可以使用任何容器,只要该容器支持empty、back、push_back、pop_back这些接口。如果没有为stack指定底层容器,默认使用deque。
| 接口声明 | 解释 |
|---|---|
explicit stack (const container& ctnr = container()) |
构造函数 |
bool empty() const |
判空 |
size_type size() const |
元素个数 |
value_type& top() |
栈顶元素 |
void push (const value_type& val) |
尾插 |
void pop() |
尾删 |
bool operator== (const stack |
关系运算 |
2.2 queue
template <class T, class Container = deque<T> >
class queue;
queue也是容器适配器。底层容器要求和stack一样。
| 接口声明 | 解释 |
|---|---|
explicit queue (const container& ctnr = container()) |
构造函数 |
bool empty() const |
判空 |
size_type size() const |
元素个数 |
value_type& front() |
队头元素 |
value_type& back() |
队尾元素 |
void push (const value_type& val) |
尾插 |
void pop() |
头删 |
bool operator== (const stack |
关系运算 |
3. OJ
3.1 最小栈
最小栈
class MinStack {
public:
void push(int val) {
st.push(val);
if (minST.empty() || val <= minST.top()) {
minST.push(val);
}
}
void pop() {
if (st.top() == minST.top()) {
minST.pop();
}
st.pop();
}
int top() {
return st.top();
}
int getMin() {
return minST.top();
}
private:
stack<int> st;
stack<int> minST;
};
准备两个栈,一个用来正常入栈出栈,一个用来存储最小值。
- 当入栈元素大于当前最小值时,只入到普通栈,不入最小栈。
- 当入栈元素小于等于当前最小值时,将其入到普通栈,也入到最小栈中。
出栈时,判断栈顶元素是否和最小值相等,相等则把最小栈中的元素也弹出。
3.2 验证栈序列
验证栈序列 / 剑指 Offer 31. 栈的压入、弹出序列
一个入栈序列对应多种出栈序列,只能拿一个栈用来模拟,如果能匹配出当前的出栈序列,则两者是匹配的。
class Solution {
public:
bool IsPopOrder(vector<int> pushV, vector<int> popV) {
stack<int> st; // 模拟栈
int popi = 0; // 出数组指针
for (auto& e : pushV) {
st.push(e); // 入栈数组只管向栈中入元素
while (!st.empty() && st.top() == popV[popi]) { // 出栈数组和模拟栈进行比较
st.pop();
++popi;
}
}
return st.empty(); // 出栈数组遍历结束或栈为空
}
};
定义一个模拟栈,定义两个指针指向出入数组的起始位置,向后遍历。
入栈数组只管向栈中入元素,只有出栈数组和模拟栈进行比较:当栈顶元素和出栈指针所指元素相等时,将栈顶元素出栈并++出栈指针。
成功示例图示
不成功示例
待入栈数组遍历结束后,若出栈数组遍历结束或栈为空,说明匹配成功,若栈中仍有元素或出栈数组未遍历结束,说明匹配不成功。
3.3 逆波兰表达式求值
逆波兰表达式求值
中缀表达式转后缀表达式的目的是,将操作符按照运算顺序从左到右依次排好,方便计算机进行运算。
中缀转后缀
遍历中缀字符串:
- 遇到操作数,直接输出。
- 遇到操作符,如果是空栈,直接入栈;如果栈非空,将其与栈顶比较优先级;
- 优先级比栈顶元素高,则入栈,比栈顶低或相等,栈顶出栈并输出。
- 遍历结束后,将栈中元素全部输出。
后缀运算
遍历后缀表达式:
- 遇到操作数,直接入栈。
- 遇到操作符,连续取两个栈顶元素(先出为右,后出为左)作操作数与其运算,运算结果入栈。
- 遍历结束后,栈顶即结果。
class Solution {
public:
int evalRPN(vector<string>& tokens) {
stack<int> st;
for (auto& s : tokens) {
if (s == "+" || s == "-" || s == "*" || s == "/") {
string optor(s); //得操作符
int op2 = st.top(); //先出为右操作数
st.pop();
int op1 = st.top(); //后出为左操作数
st.pop();
switch(s[0]) {
case '+':
st.push(op1 + op2);//将运算结果入栈
break;
case '-':
st.push(op1 - op2);
break;
case '*':
st.push(op1 * op2);
break;
case '/':
st.push(op1 / op2);
break;
}
}
else {
st.push(stoi(s)); // 操作数入栈,待遍历得操作符与之运算
}
}
return st.top();//返回栈顶元素
}
};
3.4 用栈实现队列
用栈实现队列
使用两个栈,一个用来入,一个用来出。
只要出栈为空,就将入栈中的数据全部导入出栈。只有当出栈为空时,才会导入,以免打乱顺序。保证了出栈和取数据时有元素。
class MyQueue {
public:
void push(int x) {
_pushST.push(x);
}
int pop() {
int tmp = peek(); //返回队头数据的同时进行了转移判断
_popST.pop();
return tmp;
}
int peek() {
if (_popST.empty()) { // 只需要在取数据处判断是否需要转移数据
while (!_pushST.empty()) {
_popST.push(_pushST.top());
_pushST.pop();
}
}
return _popST.top();
}
bool empty() {
return _popST.empty() && _pushST.empty();
}
private:
stack<int> _pushST;
stack<int> _popST;
};
入栈pushST和出栈popST互不影响,分别完成入队的出队的任务。只要popST为空,就将pushST中元素移入即可。
3.5 用队列实现栈
用队列实现栈
用队列实现栈,需要考虑栈是先进后出的结构,都是顺序容器插入操作一致,删除操作需要将队列中的前n-1个元素移入另一个队列,只留最后一个元素。
class MyStack {
public:
void push(int x) {
q1.push(x);
}
int pop() {
int tmp = top();
q1.pop();
swap(q1, q2);//pop之后交换,把q2变成q1,相当于栈出了栈顶
return tmp;
}
int top() {
while(q1.size() > 1) {
q2.push(q1.front());
q1.pop();
}
int tmp = q1.front();
return tmp;
}
bool empty() {
return q1.empty() && q2.empty();
}
private:
queue<int> q1;
queue<int> q2;
};
4. 模拟实现
4.1 stack
适配器是一种设计模式。数据结构栈可以用数组和链表实现,C++中栈被实现成容器的适配器,通过复用底层容器的接口。
template <class T> class stack {
void push(const T& x) {
_v.push_back(x);
}
//...
private:
vector<T> _v;
}
直接将容器 vector 作成员变量,所有接口都调用 vector 的接口即可。
template <class T, class Container = deque<T>>
class stack {
public:
void push(int x) {
_con.push_back(x);
}
void pop() {
_con.pop_back();
}
bool empty() const {
return _con.empty();
}
bool size() const {
return _con.size();
}
T& top() const {
return _con.back();
}
private:
Container _con;
};
STL直接将容器类型作为类模板参数传入,支持自定义底层容器,并采用缺省参数的形式,指定默认容器为 deque。
4.2 queue
template<class T, class Container = deque<T>>
class queue
{
public:
void push(const T& x) {
_con.push_back(x);
}
void pop() {
_con.pop_front();
}
T& front() {
return _con.front();
}
T& back() {
return _con.back();
}
size_t size() {
return _con.size();
}
bool empty() {
return _con.empty();
}
private:
Container _con;
};
queue也是容器适配器,只要按照queue的特性,将适配容器的接口换一下即可。
4.3 deque
deque的介绍
vector和list在随机访问和插入删除的方面各有优劣,为均衡二者的特性,STL设计了一种容器叫做双端队列 deque。
双端队列deque是一种双端的、“连续”空间的数据结构。双端表示可以在头尾两端进行插入和删除,且时间复杂度为O(1)。
| 增删接口 | 解释 |
|---|---|
void push_back (const value_type& val) |
尾插 |
void push_front (const value_type& val) |
头插 |
void pop_back() |
尾删 |
void pop_front() |
头删 |
| 访问接口 | 解释 |
reference operator[] (size_type n) |
随机访问 |
reference front() |
头部元素 |
reference back() |
尾部元素 |
deque的原理
deque底层并不是真正连续的空间,而是由一个中控指针数组保存每个用来存储数据的小连续空间buffer的地址。类似于一个动态的二维数组,如下图所示:
从中控数组的中部开始使用,头插使用前面的buffer,尾插使用后面的buffer。头插就向前开辟,尾插就向后开辟。
- 头部操作无需挪动数据,头插头删效率高。
- 扩容只开辟buffer,空间浪费少。
- 中控数组扩容只拷贝指针,扩容代价低。
- 先计算所在buffer再计算buffer内位置,可以支持随机访问。
如果单个buffer大小不固定,则需要迭代器支持随机访问,效率变低。
deque的迭代器有四个指针:
cur指向buffer当前数据位置first指向buffer起始位置last指向buffer结束位置node反向指向本buffer在中控数组的位置
deque的优劣
| vector的缺点 | deque |
|---|---|
| 扩容消耗高,空间浪费,头插头删效率低 | 扩容消耗低,空间浪费不严重,头插头删效率高 |
| vector的优点 | deque |
| 支持随机访问,连续空间缓存命中率高 | 支持伪随机访问,连续空间缓存命中率较高 |
| list的缺点 | deque |
| 按需申请释放,不支持随机访问 | 申请次数少,支持伪随机访问 |
| list的优点 | deque |
| 任意位置的插入删除效率高,按需申请不存在浪费 | 头尾插入删除效率高,空间浪费不严重 |
deque基本兼具两大容器的优点,缺点是中部增删效率低,且做不到两大容器的极致。
但栈和队列只需要头尾的插入删除,所以stack和queue使用deque作为默认适配容器。
deque颇具局限性,仅作了解。
5. priority_queue
5.1 接口使用
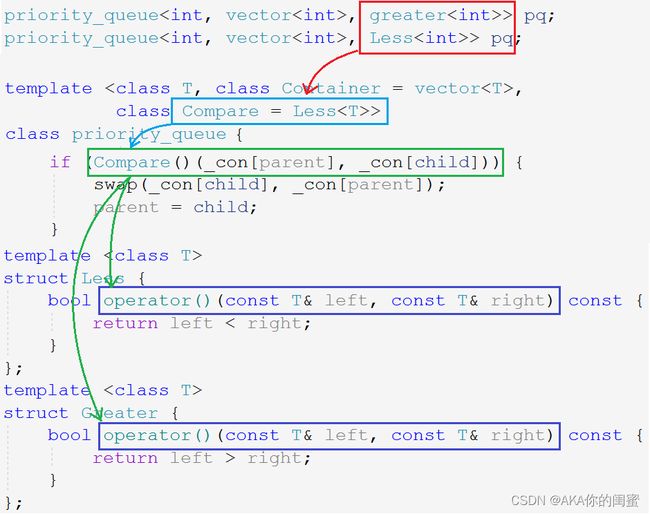
优先级队列priority_queue同样是个容器适配器,不同于stack和queue只是对容器的简单封装。它有三个模板参数:
template <class T, /* 数据类型 */
class Container = vector<T>, /* 适配容器 */
class Compare = less<typename Container::value_type> > /* 仿函数 */
class priority_queue;
priority_queue要求底层容器必须具有随机访问迭代器,支持empty,size,front,push_back,pop_back几种接口,一般使用vector作底层容器。
priority_queue就是堆,能够实现堆的各种算法。因为要维护容器本身的特性,所以不支持遍历。
class Compare = less<typename Container::value_type>
priority_queue默认数值大优先级高,也就是默认大堆。想要排成小堆,需要指定priority_queue的仿函数参数,传入greator。
| 接口声明 | 解释 |
|---|---|
priority_queue (Compare& cmp = Compare(), Container& ctnr = Container()) |
构造函数 |
bool empty() const |
判空 |
size_type size() const |
元素个数 |
value_type& top() |
栈顶元素 |
void push (const value_type& val) |
尾插 |
void pop() |
尾删 |
Top-K
class Solution {
public:
//建大堆会选出整个数组的最大值,减小堆才能选出第k大的数
int findKthLargest(vector<int>& nums, int k) {
vector<int>::iterator pos = nums.begin() + k;
//k个数的小堆
priority_queue<int, vector<int>, greater<int>> pq(nums.begin(), nums.begin() + k);
while (pos != nums.end()) {
if (*pos > pq.top()) {
pq.pop();
pq.push(*pos);
}
++pos;
}
return pq.top();
}
};
5.2 模拟实现
基本接口
template<class T, class Container = std::vector<T>, class Compare = less<T>>
class priority_queue
{
public:
void push(const T& x) {
_con.push_back(x);
adjust_up(_con.size() - 1); //向上调整
}
void pop() {
swap(_con[0], _con[size() - 1]);
_con.pop_back();
adjust_down(0); //向下调整
}
bool empty() const {
return _con.empty();
}
int size() const {
return _con.size();
}
T& top() const {
return _con.front();
}
private:
Container _con;
Compare _cmp;
};
向上向下调整算法
void adjust_up(int child)
{
int parent = (child - 1) / 2;
while (child > 0)
{
if (_cmp(_con[parent], _con[child]))
swap(_con[parent], _con[child]);
else
break;
child = parent;
parent = (child - 1) / 2;
}
}
void adjust_down(int parent)
{
int child = parent * 2 + 1;
while (child < _con.size())
{
if (child + 1 < _con.size() && _cmp(_con[child], _con[child + 1]))
child++;
if (_cmp(_con[parent], _con[child]))
swap(_con[parent], _con[child]);
else
break;
parent = child;
child = parent * 2 + 1;
}
}
堆插入就是数组尾插一个元素,然后向上调整。
此时堆的性质可能被破坏,不过只会影响该结点到根结点所在路径上的所有结点,故顺势向上调整:一直交换结点数值直到满足堆的性质即可。
堆删除就是将尾元素覆盖到堆顶,然后向下调整。
只是堆顶元素不满足性质,其左右子树还是原样。只需将堆顶元素逐步向下调整:将根结点与其较大/小的子结点交换,只要父结点比子结点中任意一个大/小,就进行交换,直到交换到叶结点或不满足条件为止。
仿函数
决定大堆还是小堆,在于向上/向下调整算法中的父子节点的比较关系:
if (_cmp(_con[parent], _con[child])) {
swap(_con[parent], _con[child]);
}
if (child + 1 < _con.size() && _cmp(_con[child], _con[child + 1])) {
child++;
}
比较大小操作符写死不便用户修改,使用宏定义,函数指针都比较复杂,还有一种简单的方式就是仿函数。
仿函数又名函数对象,本质是对象,通过重载()操作符模仿函数的调用方式。
仿函数相当于更高级的泛型,使用仿函数能够改变执行逻辑,仿函数内部的实现完全由用户自定,拥有极大的自定义空间。
template <class T>
struct less {
bool operator()(const T& left, const T& right) const {
return left < right;
}
};
template <class T>
struct greater {
bool operator()(const T& left, const T& right) const {
return left > right;
}
};
Less less;
less(1, 2);
Greater greater;
greater(1, 2);
仿函数本质是一种类型,所以可以作模版参数,让用户定义类的时候指定。
template <class T, class Container = vector<T>, class Compare = Less<T>>
class priority_queue {
void adjust_up(int child) {
if (_cmp(_con[parent], _con[child]))
//...
}
void adjust_down(int parent) {
if (child + 1 < _con.size() && _cmp(_con[child], _con[child + 1]))
//...
if (_cmp(_con[parent], _con[child]))
//...
}
Compare _cmp;
};
#include