Information Retrieval（信息检索）笔记01：Boolean Retrieval（布尔检索）

什么是信息检索（Information Retrieval）

正式定义上的信息检索（Information Retrieval）为：信息检索是从大规模非结构化数据（通常是文本）的集合（通常保存于计算机上）中找出满足用户信息需求的的资料（通常是文本）的过程。

为了避免混淆，这里我们也给出数据挖掘 (Data Mining) 的定义：
从大量的、不完全的、有噪声的、模糊的、随机的实际应用数据中，提取隐含在其中的、人们事先不知道的、但又是潜在有用的信息和知识的过程。
总的来说，信息检索 (Information Retrieval) 是帮助用户从海量信息快速找到有用信息的技术，数据挖掘 (Data Mining) 则是用于从大数据中提取出隐含的、先前未知的并有潜在意义的信息

作为一门学科，是研究信息的获取 (acquisition)、表示 (representation)、存储 (storage)、组织 (organization) 和访问 (access) 的一门学问。

这里对于数据的类型我们不再过多赘述，在数据库系统以及大数据管理中，我们已经对这方面内容有了一定的认知。我们只需记住，主要有三种类型的数据：结构化数据（Structured Data），非结构化数据（Unstructured Data）以及半结构化数据（Semi-structured Data）。其中，现实生活中最常见的就是后两者，非结构化数据的主要形式就是文本文件，而半结构化的主要形式就是XML等网页文件。

信息检索可以根据它们所处理数据的规模进行区分，主要可分为三类：

规模级别	搜索类别	主要问题
大规模	以web搜索（web search）为代表的大规模级别，需要处理存储在上百万计算机中的数十亿文件	1. 如何采集到的这种规模的文件 2. 如何针对大规模数据量建立高效运行的系统 3. 如何处理web特性带来的特殊问题
小规模	个人信息检索（personal information retrieval）代表的是个人电脑中的信息检索功能以及邮件应用中的搜索分类功能	1. 如何处理个人计算机上的各种格式的文件 2. 如何保证搜索系统的免维护 3. 如何使搜索系统占用的资源尽可能的少，不至于影响正常的工作
中规模	面向企业、机构和特定领域的搜索（domain-specific search）	文件往往存储在集中的文件系统上，由一台或者多台计算机提供搜索服务，需要兼顾前两种搜索的问题

这里我们需要注意一点，信息检索不单单是对目标的搜索和查询。用户对于文件的浏览、过滤和对返回的文件进行的处理都属于信息检索的研究范畴

我们可以用一个更简单的形式来看待信息检索 (Information Retrieval)。所谓的信息检索 (Information Retrieval) 就是给定一个查询 Q ，从文档集 C 中计算每篇文档 D 与 Q 的相关度 (Relevance) 并排序 (Ranking)。这里的相关度 (Relevance) 可以看做一个函数 R ，该函数的输入为查询 Q，文档集 C 和文档 D，输出为一个实值：R = f(Q, C, D). 因此，确定文档和查询之间的相关度是信息检索 (Information Retrieval) 的核心问题

实际生活中，对于当下主流的搜索引擎，相关度 (Relevance) 不是唯一的度量元素，其他还有诸如权威度 (Authority)，重要度 (Importance)，新颖度 (Novelty) 等，像大家常用的 Google 据说使用了上百种排名因子。

针对查询 (Query)，文档集 (Collection) 和文档 (Document) 的定义，我们会在接下来用具体的例子进行理解

布尔检索（Boolean Retrieval）

为了更好地理解布尔检索（Boolean Retrieval），首先，我们需要考虑一个具体的例子，这里我们用《莎士比亚全集》来作为一个例子。很显然，《莎士比亚全集》一书中，有着很多部作品，假如此时我们想要知道哪些作品包含 Brutus 和 Caesar 但是不包含 Calpurnia，该怎么做呢？

首先，最简单朴素的方法就是遍历。我们遍历这本书的每一部作品，去看它是否包含 Brutus 和 Caesar 但不包含 Calpurnia，并将之记录下来。这个过程也被称为 grepping，源自 Unix 下的一个文本扫描命令 grep。

但是这样简单的线性扫描明显是存在缺陷的，它难以应对以下几种情况：

1. 大规模文档集条件下的快速查找。 数据量的增长速度远高于计算机性能的增长速度，当对规模极为庞大的数据进行遍历/线性扫描时，花费的成本显然会很高
2. 有时需要更灵活的匹配方式。 在 grep 命令下，不能支持诸如 Romans NEAR countrymen 之类的查询（这里的 NEAR 操作符可能指的是“countrymen的周围5个词以内有Romans”，或者是“countrymen 和 Romains 在同一个句子中”）
3. 优选结果。 有时我们需要从所有返回的结果中采用最优答案

这个时候，我们就需要采用非线性的扫描方式去解决该问题。

什么是布尔检索（Boolean Retrieval）？

一种典型的非线性扫描方式就是建立索引（Index）。这个方法的思想很简单，很多人在大数据管理或者其他数据相关课程中应该都有所接触。

简而言之，就是我们首先统计《莎士比亚全集》这本书中一共使用了32000个不同的单词（这就是本书的Vocabulary），之后我们根据此书中的每部作品是否包含某个单词，构建一个由布尔值（0/1）构成的词项-文档矩阵（Incidence Matrix）：

在这个矩阵中，词项（Term）是索引的单位（注意，词项不一定是单词，在其他情况下，也可能是序号或者某个地点）。根据我们看待的角度不同，可以得到不同的向量：

• 从行（Row）来看：得到每个词项的文档向量，表示词项在每个文档中出现或不出现
• 从列（Column）来看：得到每个文档的词项向量，表示每个文档中出现了哪些词项

我们在这里查询 “包含 Brutus 和 Caesar 但是不包含 Calpurnia” 时，实际上可将其看做一个逻辑表达式 “Brutus AND Caesar AND NOT Calpurnia”。因此，为了响应该查询，我们只需要关注词项Brutus, Caesar 和 Calpurnia 的行向量：

Brutus = 110100 Caesar = 110111 Calpurnia = 010000

之后对 Calpurnia 向量取反：¬ Calpurnia = 101111
最后在对 Brutus, Caesar 和 ¬ Calpurnia 三个向量进行逐位与（AND）运算即可，最后的结果为：

110100 AND 110111 AND 101111 = 100100

该结果表示只有第一个作品《Antony and Cleopatra》和第四个作品《Hamlet》满足查询的条件。

通过这个例子，我们可以对布尔检索（Boolean Retrieval）有一个初步的认知，即 布尔检索模型接受布尔/逻辑表达式查询，也就是通过AND, OR 及 NOT 等逻辑运算符连接起来的查询。

接下来看一个更加现实的场景，并通过这个场景来了解一些信息检索（Information Retrieval）的术语。

假设此时我们有 N = 1,000,000 篇文档。所谓的“文档”（Documents）指的是检索系统的检索对象，它们可能是一条条单独的记录或是一本书中的各个章节（我们前一个例子中，“文档”指的就是《莎士比亚全集》中的每一部作品）。而这所有的文档组成“文档集”（Collection），也被称为“语料库”（Corpus），在之前的例子中，《莎士比亚全集》这本书就是“文档集”。

此时我们认为每个文档包含约 1,000 个词，一个词的长度为 6B，那么整个文档集的大小约为 6GB，同时，我们认为这些文档中共有 M = 500,000 个不同的词项。

针对这样一个文档集，我们想要开发一个能处理 ad hoc 检索（ad hoc retrieval）任务的系统。所谓的 ad hoc 检索任务指的是任一用户的信息需求（Information Need）通过由用户提交的一次性查询（Query）传递给系统，让该系统从文档集中返回与之相关的文档。 这里的信息需求（Information Need）指的是用户想要查找的信息主题，而查询（Query）则是由用户提交给系统以表示其信息需求，因此，对于同样的信息需求 (Information Need)，不同用户在不同时候可能会构造出不同的查询 (Query)。

为了方便理解 ad hoc ，我们在这里稍微了解一下信息检索 (Information Retrieval) 的两种模式，即 pull 和 push：

• Pull：用户主动发起请求，在一个相对稳定的数据集上进行查询，就是我们这里所说的 ad hoc，即 信息需求动态变化，而文档集则相对静止
• Push：用户事先定义自己的兴趣，系统在不断到来的数据流上进行操作，将满足用户兴趣的数据推送给用户，也就是进行过滤 (Filtering)，即 信息需求在一段时间内保持不变，而文档集则变化频繁

系统会将与用户信息需求相关（Relevant）的文档返回。而衡量检索系统质量（Effectiveness）的方法和机器学习以及其他数据科学的方法一样，仍选择使用召回率（Recall）和准确率（Precission）来进行：

• 召回率（Recall）：所有和信息需求真正相关的文档中，被检索系统返回的百分比 = TP / (TP + FN)
• 准确率（Precission）：返回结果中，真正与信息需求相关的文档所占的百分比 = TP / (TP + FP)

这个时候如果我们仍使用之前提到的词项-文档矩阵（Incidence Matrix）来构建检索系统，那么该矩阵有 N ✖ M = 1,000,000 ✖ 500,000 = 5000亿 个布尔值元素，远超一般的计算机内存容量。但实际上这个矩阵有着高稀疏性，即取1的值相比取0的值要少很多，因此我们只需要关注矩阵中取值为1的位置即可。根据这种思想，可以使用倒排索引（Inverted Index）来解决。

倒排索引（Inverted Index）

在正式开始介绍倒排索引（Inverted Index）这一技术之前，我们要先明确一个观念，这里的“倒排”只是相对于数据科学在最开始处理类似问题时的方法，那时会采用从“文档”映射到“词项”的索引方式（类似于之前提到的“列向量”）。现在看来会有些多余，因为现在的我们只要在类似问题中提到的索引，都是从“词项”反映射到“文档”，这已成为主流的索引方式。

倒排索引（Inverted Index）的思想并不复杂，用一张图就能很好地理解：

在上图中的左边，就是我们所说的词典（Dictionary，也被称为Vocabulary/Lexicon）表示整个“文档集”中出现的所有“词项”。而对每一个词项，都有一个记录出现该“词项”的“文档”的 ID 列表，该列表中的每个元素就被成为“倒排记录（Posting）”，而该列表就是“倒排记录表（Posting List）”，同时，我们一般会对该列表中的 ID 进行排序。

建立倒排索引（Inverted index construction）

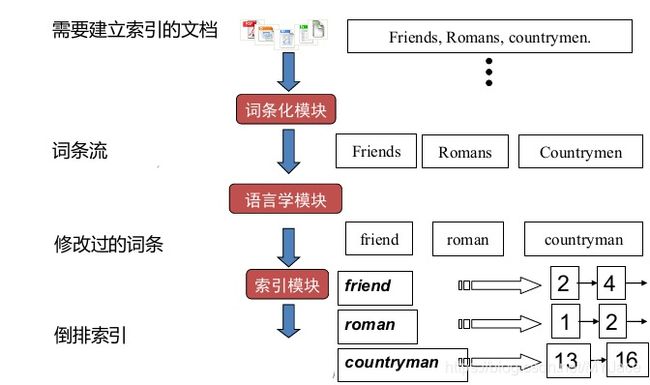
建立索引的流程也并不复杂：

1. 收集需要建立索引的文档（即收集数据集）
   

2. 将每篇文档转换为词列表，这一步通常称为词条化（Tokenization）
   

3. 进行语言学预处理，产生归一化的词条来作为词项。所谓的归一化/标准化，指的是在这一步中，一般会将文档中的词条恢复成最原始的形式，比如复数形式的词条转换为单数形式、过去式转换为一般式等，并且统一大小写
   

4. 对所有文档按其中出现的词项来建立倒排索引，按照词条排序，再按照文件 ID 排序，最终合并结果
   （下面的例子中我们还记录了词项的 DF 和 IDF）
   
   

为了方便说明，这里我用不同的色块来表示不同的内容。左边很显然就是词项词典（Dictionary）；中间的绿色表示 DF （Document Frequency），即出现某词项的文档的数量，这里也就是词项对应的倒排记录表（Posting List）的长度；红色表示文档的 ID ，蓝色则是 TF （Term Frequency），即当前文档中出现该词项的次数。我们要注意的是 DF 和 TF 对于一个基本的布尔搜索引擎不是必须的，只是它们的存在可以再处理查询时提高效率。

最终得到的倒排索引中，词典（Dictionary）和倒排记录表（Posting List）都有存储开销，前者往往存储在内存中，后者开销较大，一般存放在磁盘中。 而对于倒排记录表，有多种存储方法可以选择，比较长用的两种就是单链表（Single Linked List）和变长数组（Variable Length Array）。前者通过增加指针可以自然地进行扩展，而后者一方面可节省指针的存储开销，另一方面由于使用连续的空间存储，可利用缓存（Cache）提高访问速度。

这里我们用一张流程图总结建立倒排索引的过程：

布尔查询的处理（Query processing）

这里我们考虑一个简单的查询范例：Brutus AND Calpurnia

此时，使用了倒序索引的布尔检索系统会执行如下操作：

• 定位并返回 Brutus 的倒排记录列表（Posting）
• 定位并返回 Calpurnia 的倒排记录列表（Posting）
• 对返回的这两个列表执行“合并（Merge）”操作 （注意，这里的“合并”与传统意义的合并不同，实际上是取交集操作）

这里取交集的算法如下图所示：

用文字来描述即为：对每个有序列表维护一个位置指针，并让两个指针同时在列表中后移。每一步我们都比较两个指针所指向的文档 ID，如果两个 ID 一样，则将该 ID 添加到结果表中，然后两个指针同时向后移一步。如果 ID 不同，则将较小 ID 对应的指针后移。 因此，若两个列表的长度分别为 x 和 y，则共进行 O(x + y) 次操作，查询的时间复杂度为 O(N) （N为文档集中的文档数目）。该合并算法需要倒排记录表按照全局统一标准排序，这就是我们将它按照 ID 顺序排序的原因。

对于更复杂的查询，我们只需要扩展上述的合并算法即可。

总结一下，布尔模型可以用来处理布尔表达式形式的查询，布尔查询是用 AND, OR 和 NOT 等逻辑连接符来连接查询词汇。我们将将文档 (Document) 看作词汇的集合，模型精确返回文档是否符合条件。布尔模型也许是IR系统中的最简单的模型，但是其精确匹配 (Exact Matching) 也存在着问题，它无法具体显示出文档之间的差异，这就需要新的检索方式。

查询优化（Query Optimization）

查询优化（Query Optimization）指的是如何通过安排查询的处理过程来使处理工作量最小，这里主要指的是倒排记录表的访问顺序。 我们现在考虑一个对多个词项进行“与”操作的查询：Brutus AND Caesar AND Calpurnia

一个启发式的想法是，按照词项的文档频率（也就是DF）从小到大依次进行处理。 如果我们先合并两个最短的倒排记录表，那么所有中间结果的大小都不会超过最短的倒排记录表，这样处理所需的工作量很可能最少。这里我们就可以按照如下顺序查询：

(Calpurnia AND Brutus) AND Caesar

而对于更复杂一些的查询，比如：

(madding OR crowd) AND (ignoble OR strife) AND (killed OR slain)

我们可以获得所有词项的文档频率 （DF），由此我们可以保守地估计出每个OR 操作后的结果大小，然后按照结果从小到大的顺序执行 AND 操作。

这里给出一个例子：

对于该例子中的查询，根据 OR 操作后的结果大小：
tangerine OR trees ≈ 316812
marmalade OR skies ≈ 107913
kaleidoscope OR eyes ≈ 213312
因此，应当执行：
((marmalade OR skies) AND (kaleidoscope OR eyes)) AND (tangerine OR trees)

对于任意的布尔查询，我们必须计算并临时保存中间表达式的结果。在倒排记录表的长度相差很大的情况下，可以使用一些策略来加速合并过程。对于中间结果表，合并算法可以就地对失效元素进行破坏性修改或者只添加标记。或者，通过在长倒排记录表中对中间结果表中的每个元素进行二分查找也可以实现合并。另外一种可能是将长倒排记录表用哈希方式存储，这样对中间结果表的每个元素，就可以通过常数时间而不是线性或者对数时间来实现查找。

快速合并算法（Faster Posting List Merges）

这里我们讨论一下是否能让倒排记录表的合并操作更加高效。根据是否使用额外的数据结构，我们主要有两种方法

跳表指针（Skip Pointers/Skip Lists）

首先我们回顾一下之前使用的合并算法

可以看到，该算法是一步一步移动指针以寻求满足查询的结果。因此，它的时间复杂度为 O(x + y)。接下来，我们介绍使用跳表指针的方法（Stanford 教材和 CMS 有一些细微的差别，为了方便理解，这里我们选择使用后者的图）

其实它的概念并不复杂，我们首先要定义一个跳表指针的列表，该列表里存储了 n 个跳表指针，每个跳表指针的形式为 (d, p) ，d 表示文档 ID，p 表示位置信息。所以当指针指向 Posting List 的第一个元素之后，下一步直接跳到跳表指针指向的位置：

接下来，我们看一看跳表指针是怎样提高了合并算法的效率：

考虑以上这个具体的情境，我们仍想查询 A and B。此时，如果我们仍使用之前的合并算法，第二个列表中的指针将从 1 一步步往后移动，直到找到匹配的文档 ID / 大于 41，但在这题中，第二列表最大的元素只有31，因此，就算走完了整个列表，仍无法得出结果。为了得到答案，我们需要知道 41 是否在第二个列表中，或是要走到大于41 的最小 ID 以进行后续的计算。 这在跳表指针的帮助下就很简单了，我们只需要在指针列表中进行二分法搜索，找到符合要求的 ID，然后直接跳到其位置即可，在本题中，指针直接跳到 31，这已经是列表二的尽头，我们知道，没有结果，整个过程只移动了一次指针。

在知道了跳表指针的运作原理之后，我们需要关注的只有我们如何确定有多少个跳表指针以及如何设定跳表指针。一个启发式的方法是设置 L^1/2 个跳表指针。它可以最小化成本 要证明这个想法也很简单：

我们假设共设置了 n 个跳表指针，那么这 n 个指针平均将长为 L 的Posting List 分割为 n 的区间，每个区间长度为 L/n。每个跳表指针指向了每个区间的 Head，我们在寻找目标 ID 时，只需找到小于该 ID 的最大跳表指针，然后再以该指针起始的区间内寻找即可。

因此，整个过程的期望代价为：

f(n) = cost(pointer list) + cost(segment) = n/2 + L/2n = 1/2 * (n + L/n)

该式子中仅有一个变量 n ，为了找到 f(n) 的极限值，我们需要求导

f’(n) = 1/2 * (1 - L/n²) = 0

所以可以得到，n = L^1/2

我们需要注意的是，如果 L 相对固定的话，建立有效的跳表指针比较容易，如果索引需要经常的更新，建立跳表指针就相对困难点。

这里还有一个细节值得我们注意，在访问 Skip Pointers 的列表时，我们总需要比目标指针再多访问一个指针。比如我们的目标文档 ID 是 31，而 Skip Pointers 列表为 {(27, …), (35, …)}。我们知道，比 31 小的最大指针指向 27，但我们仍需要知道 27 之后为 35，才能确定 27 是我们要的答案。

这一部分的内容，我会单独用另一篇博客来进行更为详细的介绍：
补充内容

含位置信息的倒排记录表及短语查询（Phrase Queries and Positional Indexes）

在以上内容中，我们介绍的多为词与词组成的逻辑语句的查询，这些词之间可以很独立。但在现实生活中，我们实际上经常需要进行短语查询 (Phrase Query)，比如：机构的名称、技术性概念、人名等。这个时候，再使用之前的布尔查询 (Boolean Query) 是很难获得比较理想的效果的。

比如我们想要查询 Stanford University，这时我们自然是想把这两个词看作一个整体来进行查询。因此，我们绝对不想系统返回一篇有以下句子的文章：
The inventor Stanford Ovshinsky never went to university
可以看到，这篇文章虽然包含 Stanford 和 University，但并没有将其看作一个短语进行整体匹配

目前，大部分的搜索引擎都支持双引号语法进行短语查询（比如 “Stanford University”）。现实中，很多用户在进行短语查询时，并没有加引号的习惯，但搜索引擎仍给出了正确的应答，这是因为它们进行了隐式的短语查询。这一节，我们介绍两种短语查询的方法以及混合使用二者实现的高效短语查询方法。

二元词索引（Biword Indexes）

二元词索引就是将文档中的每个连续词对 (Consecutive Pair) 看作一个短语，比如文本 “Friends, Romans, Countrymen” 会产生以下二元词 (Biword)：friends romans, romans countrymen。现在，我们将每个二元词作为字典 (Dictionary) 中的词项 (Terms)，这样就能立刻处理两个词构成的短语查询，更长的查询可以分成多个短语来查询。

比如：stanford university palo alto 可划分为如下布尔查询：
“stanford university” AND “university palo” AND “palo alto”

但我们要注意，该查询可能会返回 False Positive 结果。 因为对于该查询返回的文档，我们并不知道其是否真正包含最初始的四词短语 (“stanford university palo alto”)。在所有可能的查询中，名词短语占据重要的一席之地，但是实际中，名词往往被各种虚词分开，比如 glory of the champion。因为，接下来，我们将介绍一种扩展二元词索引 (Extended biword indexes) 方法。

扩展二元词索引 (Extended biword indexes) 首先对文本进行此词条化，然后进行词性标注 (Part-Of-Speech-Tagging, POST) 。 这样，我们将词项归为名词 (记为 N，包括专有名词)、虚词 (记为 X，包括冠词和介词) 和其他词。然后将所有形式为 NX*N 的非词项序列看作一个扩展二元词，每个这样的扩展二元词，对应一个词项

比如：glory of the champion
glory → N, of → X, the → X, champion → N
此时，该扩展二元词对应的词项为 glory champion，在索引中进行查找

二元词索引存在着一些缺陷，

• 首先就是我们之前提及的，使用该方法会返回 False Positive 结果。
• 其次，该方法对于单个词的查询不是很方便。因为需要扫描整个 Dictionary 来寻找所有包含该单词的二元词。
• 在存储更长的短语时，很可能会大大增加 Dictionary 的尺寸。

位置信息索引（Positional Indexes）

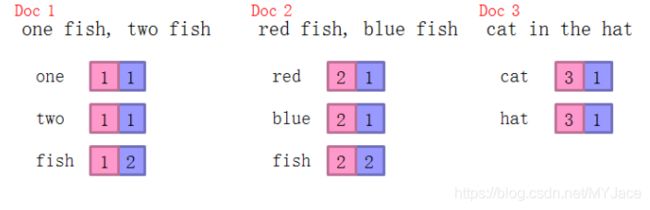
很显然，基于上述提及的缺点，二元词索引并非标准的解决方案。实际中，更常用的是另一种方法，即位置信息索引 (Positional Indexes)。在该索引中，以如下方式存储倒排表：

文档 ID：(位置1, 位置2, … )

也就是我们对 Posting List 中的元素进行扩充。原本 Posting List 中的每个元素是一个文档 ID，此时我们不仅要记录文档 ID，还要记录下该此项当前文档中的位置信息。注意，这里我们还记录了该词项在对应文档的 IDF

此时对短语查询进行处理的话，仍要先访问每个词项的 Posting List，可以和之前一样，根据 DF 小的词项优先操作的策略来减少计算量。在合并操作中，我们不单单只是找到同时包含两个词项的文档，还需要检查这两个词项在该文档中的位置关系 (偏移距离) 和查询短语的一致性。

但是在这里，我们也能发现，使用位置信息索引的方法，也会大大增加 Posting List 的存储空间。同时，采用位置索引会增加 Posting List 合并操作的渐进复杂性，这是因为需要检查的项的个数不再受限于文档数目而是文档集中出现的所有的词条的个数T。也就是说，此时布尔查询的复杂度为 Θ(T) 而不是 Θ(N)。但是这种短语搜索以及邻近搜索 (Proximity Queries) 在现实中的需求很高，所以大部分应用不得不使用这种方法。

现在具体看看位置索引的空间消耗。位置索引需要对每一个词项的每次出现保有一个记录，因此，索引的长度往往取决于文档的平均长度。如果我们假设一个词项的平均出现率为 1/1000，那么，对于普通倒排记录表的索引和位置信息索引，我们能够得到以下结果：

这很好理解，因为普通的倒排记录表只记录该文档是否包含该词项，因此对该文档的记录永远都只有其文档 ID，而位置信息索引需要记录该词项在当前文档中的每次出现。

尽管确切的数字要视文档及其语言的具体类型而定，但是利用一些粗略的经验法则可以预期位置索引大概是非位置索引大小的2～4 倍，而压缩后的位置索引大概为原始未压缩文档文本（去除标记信息）的1/3～1/2。

混合索引机制（Combination schemes）

二元词索引 (Biword Indexes) 和位置索引 (Positional Indexes) 这两种策略可以进行有效的合并。假如用户通常只查询特定的短语，如Michael Jackson，那么基于位置索引的倒排记录表合并方式效率很低。因此出现了一种混合使用的策略：对某些查询使用短语索引或只是用二元词索引，对其他短语查询则使用位置信息索引。 那么，我们就需要明确，哪些短语该使用那种方法：

• 短语索引/二元词索引一般收录那些高频常见的查询，这些都能够从用户最近的活动日志中采集得到

但这并不是唯一的准则。一般系统中处理开销最大的短语查询，往往是一些冷僻组合，比如我们可以将 Michael Jackson 加入到短语索引的话大概有3倍左右的提速效果，单若将 The Who 加入的话，加速效果可能会更显著。

2004年时，Williams 等人评估了一个更复杂的混合索引机制，其中除了包含上面两种形式的索引外，还在它们之间引入了一个部分后续词索引（next word index），即对每个词项，有个后续词索引记录了它在文档中的下一个词项。论文的结论是，虽然比仅仅使用位置索引增加了26%的空间，但是面对典型的Web 短语混合查询，其完成时间大概是只使用位置索引的1/4。