动态规划 dp dynamic planning

01背包

动态规划是一个很常考的题目，经常经常考，求职面试，还是笔试、机试都会考到这个。那么，什么是动态规划呢？先来看看动态规划的经典问题，感受一下。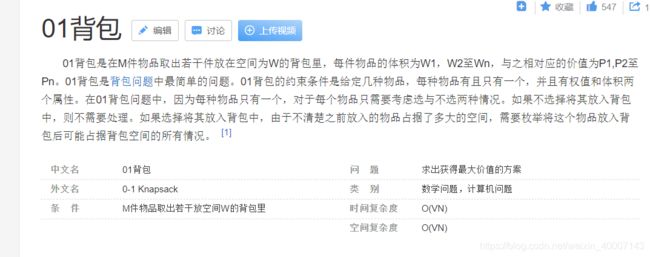

一看这种题目吧，就知道它比较的麻烦，因为我们要一个一个的尝试，最终才可以确定下来，是哪种方案最好。那么，对于计算而言，“试试”就意味着要循环，循环虽简单，但是复杂度很高，一般我们都要进行优化。好了，先来看看，基础版的循环怎么写。
先确定，我们是要算出，背包的最大价值，也就是装了尽可能多的东西之后，总价值最大是多少。那么，要用循环来遍历不同的背包容量下，存放不同重量的物品，背包可以达到的最大价值，既然是要循环遍历，那就要考虑中间是不是会有很多的数据是重复的，不需要反复计算的，这些数据可以用数组存储下来的。这句话是重点，因为这样我们就比普通的循环遍历效率高了，（当然，这里利用数组记录中间数据的方法和前面提到的优化递归的方法本质上是一样的，所谓的记忆搜索。）记住，大多数的dp问题，都要用到一个数组来记忆中间数据。好了，现在数组定义好了，那么数组里的元素表示什么含义呢？一般而言，题目要求什么，就可以定义为什么含义。比如，这里要求最大的价值，就可以定义一个二维数组B,那么B[i][j]就表示，计算到第j个物品的时候，当背包容量为j的时候，此时的最大价值。问题已经解决了一大半了，还剩最后一步，和递归类似（要找子问题，），这里是要找数组间元素的关系式，所谓的“关系”，我们要自己分析题意，才能慢慢的发现。对于本题，显然，当面对第i个物品的时候，我们可以考虑放入或者不放入两种，不同的方法下，背包的价值是不一样的，这里我们显然是取二者的较大值。
好了，分析清楚了，请看代码。

#include
using namespace std;

int w[6] = {0,2,3,4,5,6};
int v[6] = {0,4,5,6,7,8};
int B[6][21] = { 0 };
int N = 6;
int M = 21;
void knapsack() {
	int n;
	int m;
	for (n = 1; n < N; n++) {
		for (m = 1; m < M; m++) {
			if (w[n] > m) {
				B[n][m] = B[n - 1][m];
			}
			else {
				int value1;
				int value2;
				value1 = B[n - 1][m-w[n]] + v[n];    //放入
				value2 = B[n - 1][m];   //不放入。
				if (value1 > value2) {
					B[n][m] = value1;
				}
				else { B[n][m] = value2; }
			}
		}
	}
}

int main() {
	knapsack();
	cout<<B[5][20];
	return 0;
}

这是最基本的，未经过优化的。看着比较容易懂。这里推荐一个视频。里面的背包生成器不错。
接下来，要考虑优化了，优化怎么优化呢，只有一个技巧，那就是画图，画出定义的数组，一般二维数组可以优化到一维。画出二维数组，然后仔细分析，计算的过程中，到底是怎么搞的，找到规律。关于0-1背包问题的优化，我专门写过文章。请移步

dp

好了，看完了一道例题，我们了解了dp的“样子”，就是那种大问题的求解，比较复杂，要去“试”的那种，一般就是用dp来解。那你可能要说，“试”的题目，还可以用递归、回溯、搜索等等方法啊。是的，对的，下面来具体分析一下。回溯是一种特殊的搜索，要回到原来状态的那种搜索，递归是可以看出来明显的子问题，这里的dp呢，适合在多条搜索路径求最值。
一维dp的经典例子：

二维dp的经典例子：

当然，这些例子在leetcode里面都有代码，也可以参考这位大佬的文章。这里

凑零钱

先给出一个递归求解的代码，这种题目吧，一看到有子问题，就可以联想到递归求解。这里的代码里面，还有一个特点，就是使用了一个数组来记录搜索过的值（备忘录或者叫记忆搜索都可以）。

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int>memo(amount+1,-3);
        return helper(coins,amount,memo);
    }
    int helper(vector<int>&coins,int amount,vector<int>&memo){
        if(amount==0) return 0;
        if(memo[amount]!=-3){return memo[amount];}
        int ans=INT_MAX;
        for(int coin:coins){
            if(amount-coin<0) continue;
            int subProb=helper(coins,amount-coin,memo);
            if(subProb==-1) continue;
            ans=min(ans,subProb+1);
        }
        memo[amount]=(ans==INT_MAX)?-1:ans;
        return memo[amount];
    }
};

这道题，要求的“最”值，就可以联想到动态规划。在上面的例子中，求11的最小组合，可以转换为求10 9 和6最小组合 的子问题。当然了，这里求的就是这三个子问题的最值。因此，我们可以根据这个分析来写dp的代码。

class Solution {
public:
    int coinChange(vector<int>& coins, int amount) {
        vector<int>dp(amount+1,INT_MAX-10);
        dp[0]=0;
        for(int i=1;i<dp.size();i++){
            for(int coin:coins){
                if(i-coin<0) continue;
                dp[i]=min(dp[i],dp[i-coin]+1);
            }
        }
        return (dp[amount]==INT_MAX-10)?-1:dp[amount];
    }
};

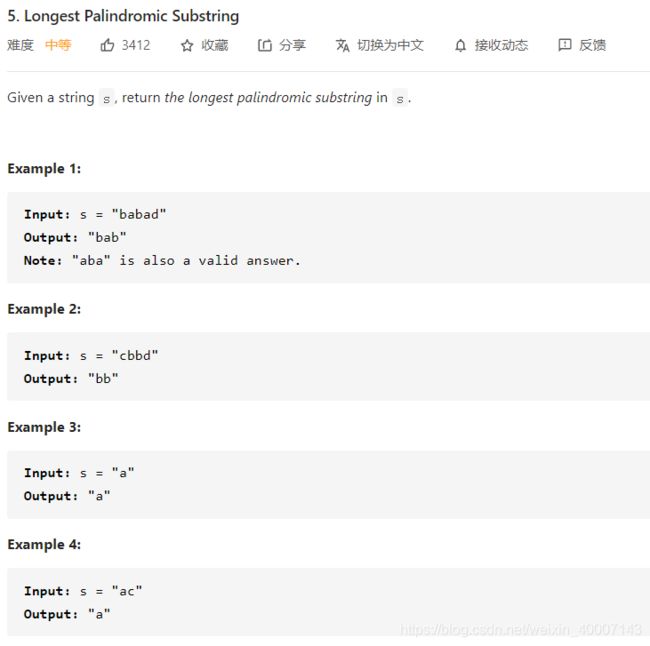
最长回文子串

这道题，比较难，这是要找最长的那个回文字符串，既然是最长。最值，马上联想到动态规划。好了，这道题的动态规划，怎么分析呢？先假设数组，数组dp[i][j]的元素含义是字符串从第i个元素到第j个元素是不是回文串。好了，接下来是关系，这里的关系式怎么样的呢？字符串从第i个元素到第j个元素是回文串,当且仅当字符串从第i+1个元素到第j-1个元素是回文串，且第i个元素和第j个元素相同。对，就是这个，我们找到了，接下来就是边界处理，也就是当字符串的长度为1和2的时候，我们单独判断一下是不是回文串就可以了。

class Solution {
public:
    string longestPalindrome(string s) {
        int n=s.size();
        vector<vector<int>> dp(n,vector<int>(n));
        string ans="";
        for(int len=1;len<n+1;++len){
            for(int i=0;i+len<n+1;++i){
                int j=i+len-1;
                if(len==1){
                    dp[i][j]=1;
                }
                else if(len==2){
                    dp[i][j]=(s[i]==s[j]);
                }
                else dp[i][j]=(s[i]==s[j]&&dp[i+1][j-1]);
                if(dp[i][j]&&len>ans.size()){
                    ans=s.substr(i,len);
                }
            }
        }
        return ans;
    }
};